1. Предмет і метод фізики та її зв'язок з суміжними науками

Название	1. Предмет і метод фізики та її зв'язок з суміжними науками
Анкор	Shpori.docx
Дата	11.08.2018
Размер	1.26 Mb.
Формат файла
Имя файла	Shpori.docx
Тип	Документы #22815
страница	4 из 8

1 2 3 4 5 6 7 8

Третій закон термодинаміки

Теорема Нернста базується на квантовомеханічних уявленнях. У класичній фізиці ентропія визначена з точністю до сталої, тому можна стверджувати лише те, що при нульовій температурі ентропія приймає мінімальне значення. Згідно з квантовою механікою при абсолютному нулі температури фізичне тіло перебуває в основному стані. Такий стан єдиний. Оскільки

,

де S — ентропія, k — стала Больцмана, Γ — кількість можливих станів, ентропія системи дорівнює нулю.

Ідеа́льний газ (рос. идеальный газ; англ. ideal gas, нім. ideales Gas n) — це газ, в якому молекули можна вважати матеріальними точками, а силами притягання й відштовхування між молекулами можна знехтувати. У природі такого газу не існує, але близькими за властивостями до ідеального газу є реальні розріджені гази, тиск в яких не перевищує 200 атмосфер і які перебувають при не дуже низькійтемпературі, оскільки за таких умов відстань між молекулами набагато перевищує їх розміри.

Рівн́яння стáну ідеáльного гáзу — формула, що встановлює залежність між тиском, молярним об'ємом і абсолютною температурою класичного ідеального газу. Рівняння має вигляд:

$p\cdot v_\mu = r\cdot t$ , де:

— тиск,
— молярний об'єм,
— абсолютна температура,
— універсальна газова стала.

Оскільки , де  — кількість речовини, то рівняння можна записати у вигляді:

$\frac{p\cdot v}{t} = \nu\cdot r$

$\frac{p\cdot v}{t} = \text{const}$

Останнє рівняння називають об'єднаним газовим законом. З нього випливають закони Бойля—Маріотта, Шарля і Гей—Люссака:

$p = \text{const} \rightarrow \frac{v}{t} = \text{const}$ — закон Гей-Люссака

$v = \text{const} \rightarrow \frac{p}{t} = \text{const}$ — закон Шарля (другий закон Гей-Люссака)

$t = \text{const} \rightarrow p\cdot v = \text{const}$ — закон Бойля-Маріотта

Закон Бойля—Маріотта названий на честь ірландського фізика, хіміка і філософа Роберта Бойля (1627—1691), що відкрив його в 1662, а також на честь французького фізика Едма Маріотта (1620—1684), який відкрив цей закон незалежно від Бойля в 1676 році. Якщо записати , де m — маса,  — молярна маса, рівняння стану виглядатиме так:

$pv=\frac{m}{\mu}rt$

Ця форма запису носить назву рівняння (закона) Клапейрона—Менделєєва.

Інша форма запису, яка частіше використовується в статистичній фізиці:

$pv = n k_b t \,$ ,

де N — кількість частинок,  — стала Больцмана.

Її можна також переписати у вигляді

,

де n = N/V — густина частинок.

31. Рівняння стану ідеального газу.

При вивченні зміни стану важливо встановити зв’язок між різними величинами, що характеризують властивості речовини і називаються параметрами стану. Найважливішими з них є густина (або зв’язаний з нею питомий об'єм, що займає одиниця маси речовини), тиск і температура.

Рівняння, що зв’язує для певної маси речовини об'єм, тиск і температуру, називають термічним рівнянням стану речовини, яке надалі називатимемо рівнянням стану. Запишемо це рівняння у загальному вигляді

F(p,v,t)=0

Найпростішого вигляду рівняння стану набирає для ідеального газу. Ідеальний газ — це фізична абстракція (модель), яка реально не існує, але з якою порівнюють реальні гази.

Під ідеальним газом розуміють такий газ, у якому частинки між собою на відстані не взаємодіють, а розмірами їх можна нехтувати, тобто вважати, що маса їх зосереджена в точці. Реальні гази поводять себе як ідеальний газ при високих температурах й малих тисках. Однак практично деякі гази навіть при атмосферному тиску і кімнатній температурі в першому наближенні можна характеризувати законами ідеального газу. Закони ідеального газу виведені для незмінної маси газу.

Закон Бойля — Маріотта справедливий за сталої температури (ізотермічний процес):

Pv=const

Закон Гей-Люссака передає залежність об’єму газу від температури при сталому тиску (ізобарний процес):

V=Vo(1+at)

де α = 1/273 К^-1 — термічний коефіцієнт об’ємного розширення.

Закон Шарля характеризує залежність тиску газу від температури при сталому об’ємі (ізохорний процес):

P=Po(1+at)

Аналізуючи рівняння (4.2)—(4.4), можна дістати об’єднаний газовий закон:

P1V1/T1=P2V2/T2=…...=PnVn/Tn

Фізичний зміст цієї формули такий: якщо помістити газ у закриту посудину, об’єм якої можна змінювати, наприклад у циліндр з поршнем, то при довільній зміні об’єму й температури тиск змінюватиметься так, що відношення добутку тиску на об’єм до абсолютної температури дорівнюватиме деякій сталій величині. Ця величина, як показує досвід, залежить від маси газу.

Для грам-моля будь-якого газу це відношення буде таким:

PV=Rt

де R — універсальна газова стала [(в СІ R - 8,31 Дж/(моль ∙ К), в системі СГС R = 8,31 ∙ 10⁷ ерг/ (моль ∙ К)].

Рівняння (4.6) називають рівнянням Менделєєва — Клапейрона. Найбільш загальна форма цього рівняння для довільної маси газу m така:

PV=(m/ μ)*RT

PV=nRT

де μ — молярна маса газу; n — число молів газу.

32. Основне рівняння МКТ

Подібно до використання в механіці ідеалізованого поняття матеріальної точки, в молекулярній фізиці використовують поняття ідеального газу як величезної сукупності матеріальних точок, які не взаємодіють одна з одною на відстані.
За умови достатньо низького тиску і високої температури реальні гази (азот, кисень та ін.) за своїми властивостями близькі до моделі ідеального газу.
Основним рівнянням МКТ ідеального газу є математичний вираз тиску газу через концентрацію його молекул n=N/V (де V — об’єм), масу кожної молекули m0(m нульове) і квадрат середньої швидкості молекули: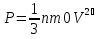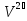

(

) вектор

33.Тиск газу точки зору молекулярно кінетичної теорії.

Вихідні положення:

Розглянемо одноманітний ід. Газ
Напрям руху молекул рівно ймовірний (основа твердження- однаковий тиск на стінки сосудів)
Хаотичний рух молекул заміняють рухом вздовж трьох взаємно перпендикулярних напрямків всі молекули рухаються з однаковою швидкістю

N-число молекул які на три осі в двох напрямках

n- концентрація молекул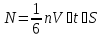

34. Молекулярно-кінетичне пояснення температури.

Молекулярно-кінетична теорія виходить із того, що речовина, зокрема газ складається з великої кількості мікроскопічних частинок (молекул), які рухаються хаотично. Частинки стикаються між собою та зі стінками посудини, створюючи на ці стінки тиск. Усі зіткнення вважаються пружними, тобто проходять без втрати енергії. Середнякінетична енергія руху частинок залежить від температури.

Середня кінетична енергія руху молекули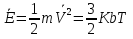

де m — маса частинки, v — її швидкість, Kb — стала Больцмана, T — температура.

35.Внутрішня енергія термодинамічної системи. Робота як форма передачі енергії. Кількість теплоти.

Вн́утрішня ене́ргія тіла (позначається як E або U) — повна енергія термодинамічної системи за винятком її кінетичної енергії як цілого і потенціальної енергії тіла в полі зовнішніх сил. Внутрішня енергія складається з кінетичної енергії хаотичного руху молекул, потенціальної енергії взаємодії між ними і внутрішньомолекулярної енергії.

Внутрішня енергія є однозначною функцією рівноважного стану системи. Це означає, що кожний раз, коли система опиняється в даному рівноважному стані, її внутрішня енергія приймає властиве цьому стану значення, незалежно від передісторії системи. Отже, зміна внутрішньої енергії при переході з одного стану в інший буде завжди дорівнювати різниці значень в цих станах, незалежно від шляху, по якому здійснювався перехід. Внутрішню енергію тіла не можна виміряти напряму. Можна визначити тільки зміну внутрішньої енергії: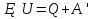

де Q — кількість теплоти, передана термодинамічній системі,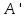

— робота, виконана над термодинамічною системою^[1] або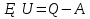

:

де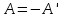

, робота виконана термодинамічною системою.

При усіляких взаємодіях енергія передається від одних тіл до інших. У випадку якщо тіло ізольоване, його енергія залишається постійною в часі. Існують дві форми передачі енергії від одного тіла до іншого: робота і теплопередача.

Роботою називається та форма передачі енергії, що супроводжується передачею імпульсу. Всяка інша форма передачі, що не супроводжується силовим впливом, називається теплопередачею.

Передана в процесі роботи енергія також називається роботою, а передана в процесі теплопередачі енергія називається кількістю теплоти. Таким чином, робота і кількість теплоти – родинні поняття. Те й інше виражає собою передану енергію (а не енергію, що утримується в тілі), але тільки передану різними способами.

Робота, як форма передачі енергії.

Проаналізуємо поняття роботи. Отже, робота є насамперед зміною енергії тіла. З визначення роботи випливає основна формула, на яку часто доводиться спиратися при розв’язуванні задач: A=E2-E1

Кількість теплоти.

Кількість теплоти або кількість тепла — це фізична величина, яка характеризує процеси обміну енергією між тілами при теплообміні. Кількість теплоти є однією з основних термодинамічних величин.

Позначається зазвичай літерою Q, має розмірність енергії. В системі СІ вимірюється вДжоулях, проте доволі часто використовують позасистемну одиницю вимірювання —калорію.

Кількість теплоти, яка передається тілу, або відбирається від тіла в зворотніх рівноважних процесах, можна визначити із першого закону термодинаміки: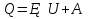

де Q — кількість теплоти, отриманої тілом, ΔU — зміна його внутрішньої енергії, A —робота, виконана тілом над іншими тілами.

В статистичній фізиці кількість теплоти, отриманої тілом при переході між двома близькими макроскопічними станами, визначається, як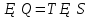

,

де T — температура, ΔS — термодинамічна ентропія.

36.Теплоємність.

Пито́ма теплоє́мність (c) — кількість теплоти, яку необхідно надати одиниці маси, щоб нагріти її на 1°C, або ж кількість теплоти, що виділяється при охолодженні одиниці маси речовини: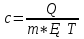

,

де Q — кількість теплоти, отримана речовиною при нагріванні (або, що виділилася при охолодженні), m — маса речовини, що нагрівається (або охолоджується), ΔT — різниця кінцевої і початкової температур речовини.

Позначається здебільшого літерою c (для теплоємності тіла будь-якої маси зазвичай використовується велика літера C). В СІ питома теплоємність вимірюється уДж/кг·К або Дж/кг·°C.

Кількість теплоти, необхідна для нагрівання будь-якого тіла на один градус називається теплоємністю тіла і знаходиться за формулою: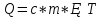

,

де m — маса речовини, c — питома теплоємність, ΔT — різниця кінцевої і початкової температур речовини.

Використовується також поняття молярної теплоємності — це кількість теплоти, яку необхідно надати молю речовини, щоб нагріти його на один градус. Одиниця виміру в системі СІ — Дж/(моль·К).

37. Перший закон термодинаміки.

Перший початок термодинаміки часто формулюють як неможливість існування вічного двигуна 1-го роду, який здійснював би роботу, не черпаючи енергію з якого-небудь джерела.

Зміна внутрішньої енергії закритої системи, яка відбувається в рівноважному процесі переходу системи із стану 1 в стан 2, дорівнює сумі роботи, зробленої над системою зовнішніми силами, і кількості теплоти, наданої системі: ΔU = A' + Q. Робота здійснена системою над зовнішніми тілами в процесі 1->2 (Назвемо її просто А) A=-A', тоді закон приймає вигляд: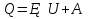

.

Кількість теплоти, що надається системі, витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил.

Для елементарної кількості теплоти δQ; елементарної роботи δA і малої зміни dU внутрішньої енергії перший закон термодинаміки має вигляд: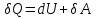

38.Другий закон термодинаміки. Цикл Карно.

1 2 3 4 5 6 7 8