Ответы к Колойдной химии экзамен, Мирэа тхт. Все лекции по колде. 1. Предмет коллоидной химии. Почему поверхностные явления и дисперсные системы изучают в рамках одной дисциплины коллоидной химии Значение коллоидной химии для технологии
 Скачать 2.71 Mb.
|
|
14. Поверхностная активность по Ребиндеру. Графическое определение поверхностной активности. Ребиндер рассматривал  поверхностная активность (   Дж м/ моль) (Н м2/моль) (Гиббс). Физический смысл поверхностной активности- сила удерживающая вещество на поверхности и рассчитанная на единицу Гиббсовской адсорбции.  σ0 g=tg(180-α) g=-tgα  α с15. Сталагмометрический и тензиометрический методы исследования поверхностного натяжения. Сталагмометрический метод основан на измерении массы капель Р, образующихся при вытекании жидкости из вертикальной трубки с радиусом выходного отверстия r. Расчет проводят по формуле  где f (r/a) – некоторая функция, определяемая из таблиц Гаркинса и Брауна; а – капиллярная постоянная.Если жидкости хорошо смачивают материал капилляра, то, пренебрегая различием между углами смачивания, можно проводить относительное измерение поверхностного натяжения , используя стандартную жидкость. В этом случае обычно принимают, что масса капли Р в момент отрыва пропорциональна поверхностному натяжению на границе раздела жидкость–пар, т.е.Р = ks , где k – постоянная данного прибора. Массу одной капли определяют, подсчитывая число капель (n), вытекающих из сталагмометра объемом V:  . Сталагмометра представляет собой сферический пузырек известного объема Vk, ограниченный метками b и d и соединенный с двумя калиброванными капиллярами, имеющими объем каждого деления vе. Сталагмометр заполняют жидкостью, затем позволяют мениску очень медленно перемещаться по капилляру, перекрывая частично доступ воздуха в капилляр с помощью резиновой трубки и зажима таким образом, чтобы каждая капля образовывалась за время не менее 4 с. После падения первой капли проводится отсчет деления, соответствующего верхнему мениску в капилляре (n делений от метки). Скорость последующего образование капель также контролируют и устанавливают время образования капли не менее 4–5 с. После достижения мениском метки, например e в нижнем капилляре C (m делений от метки d), определяют объем одной капли при числе подсчитанных вытекших из сталагмометра капель N. Недостаткам сталагмометрического метода можно отнести возможность испарения жидкости с поверхности капель при их длительном образовании и необходимость введения поправочных коэффициентов для точного определения поверхностного натяжения. 16. Переход от изотермы поверхностного натяжения к изотерме адсорбции графическим методом, расчет величины Гмах с помощью уравнения Ленгмюра.  σ tgα=-(z/c)= Г с/Г сtgα=Гмах Г Г=ГмахКС/1+КС =-(dσ/dc) α Гмах→S0= z Г=  =1/ГмахNa→δ0=МГмах/ρ с c c c 17. Влияние на адсорбцию на границе раствор-газ строения и размера молекул ПАВ. Правило Траубе, его аналитическое выражение и физическое обоснование. Правило Дюкло-Траубе. Величина поверхностной активности (g) ↑ при ↓ полярности углеводородного радикала. g в гомологическом ряду ПАВ изменяется в геометрической прогрессии при увеличении длины цепи в арифметической прогрессии. При увеличении длинны цепи ↓ растворимость ПАВ и ↑ адсорбция.  σ Г Гмах=const σ0 уксусная кислота(С2) С5 пропионовая кислота (С3) С4 масляная к-та(С4) С3 валериановая кислота(С5) С2 с с При увеличении длинны цепи в гомологическом ряду алифатического соединения на одну группу СН2, поверхностная активность ↑ в 3,2 раза( относится к водным растворам при комнатной температуре) Аналитическое выражение  qn+1/qn=3.2Кn+1/Kn=3.2. Физический смысл А=RTlnK. Работа адсорбции- работа обратимого переноса 1 моля вещества из объема в 1 поверхностный слой. An+1-An=RTlnKn+1-RTlnKn= =690кал/моль Кn+1/Kn=3.2. сущность этого правила состоит в том, что работа адсорбции на каждую группу СН2-const=690кал/моль. 1  8. Уравнение Шишковского, связь с его помощью уравнений Ленгмюра и Гиббса.σ σ0 1 2 3 1 и 3- прямые 2-переходный σ=σ0-σ0Bln(C/A +1) константа В- постоянная величина в ряду гомологов В=0,15-0,3; const 1/А- удельная капиллярная с постоянная , изменяется в ряду гомологов ак же как на поверхностно активных. 1-«С» мала ln(C/A +1)≈C/A σ=σ0-σ0BlnC/A -d σ= σ0B (dC/A) -(dσ/dC)≈1/A. Определение константы уравнения Шишковского , рассмотрим участок 2: σ=σ0-σ0BlnC/A- уравнение прямой линии в координатах σ lnC.  -ln(1/A) σ tgα=-σ0β→tg(180-α)= σ0β→если σ=σ0, то σ0BlnC/A=0→lnC=-ln(1/A)σ 0 →Гмах=  K=1/A  Связь уравнений Ленгмюра и Гиббса с α помощью уравнения Шишковского:  lnC  разделим и проинтегрируем σ=σ0-ГмахRTln(1+КС)→ГмахRT=σ0B. K=1/A.т.о., у-ния, описывающие изотермы адсорбции и поверхностного натяжения, взаимосвязаны между собой.( к 19).19. Построение изотермы адсорбции по изотерме поверхностного натяжения расчетным путем с помощью уравнения Шишковского. Связь между константами уравнения Шишковского и Ленгмюра.(см 18) Переход от уравнения Гиббса к уравнению Ленгмюра с lnC α помощью уравнения Шишковского:  -dσ=σ0-σ0Bln(C+A)= σ0В-(dC/C+A)   -показывает общность теории адсорбции, вывод на основании разных представлений. 2-ой вид уравнения Шишковского:σ=σ0-ГмахRTln(1+КС)20. Строение адсорбционных пленок на жидкой поверхности. Диаграммы строения поверхностных пленок. Пленка ПАВ может находится в 3-х агрегатных состояниях:1)тв2)ж3)г. агрегатное состояние зависит от концентрации ПАВ и длины углеводородного радикала.  Г Ж ТВ π f а-в- сжатие газовой пленки π в-с- переход из газа в жидкость Лауриновая кислота сd- сжатие жидкой пленки (только газ) d-e- переход из Ж в ТВ нерестиновая к-та e-f- разрушение или (газ-жидк) колапсс пленки полиметиновая к-та(ТВ) Sм Sм 21. Вывод уравнения состояния двухмерного газа. Уравнение Фрумкина для реального двухмерного газа. π- поверхность давления в пленке, π= σ0- σ=КС→d π=-d σ=KdC  у-ние состояния двухмерного газа. Для реального газа- у-ние Фрумкина  22. Адсорбция на границе твердое тело-газ. Теория мономолекулярной адсорбции Ленгмюра. Вывод и анализ уравнения изотермы мономолекулярной адсорбции Ленгмюра. Адсорбция на границе газ-тв тело- простейший вид адсорбции. А-f(T,P,Sуд). Газ при адсорбции может передвигаться только в 2-х измерениях и адсорбция сопровождается ↓ энтропии.ΔF↓ 0<ΔF=ΔH-TLS ΔS↓0 ΔH<0→+Q- самопроизвольная адсорбция, является экзотермическим процессом. Теория Ленгмюра. Допущения:1) адсорбция локализована , а силы близки к химическим 2)адсорбция протекает только на активных центрах 3)радиус действующих адсорбционных сил мал, и 1 активный центр адсорбирует только одну молекулу 4)в определенный момент времени устанавливается динамическое равновесие между адсорбцией и десорбцией 5)между адсорбирующимися молекулами отсутствует взаимодействие. Адсорбцию можно рассматривать как квазихимическую реакцию. Молекула газа(Р)+активный центр(А0)<=>адсорбционный комплекс(А). А  =КРА0; Амах=А0+А; А=КР(Амах-А); А=КРАмах-КРА; А=(АмахКР)/(1+КР)-у-ние Ленгмюра для изотермы мономолекулярной адсорбции.А 1 2 3 1: А=АмахКР 2: А=(АмахКР)/(1+КР) 3: А=Амах У-ние Ленгмюра описывает все 3 участка изотермы адсорбции Р 23. Линейная форма уравнения Ленгмюра. Нахождение констант уравнения Ленгмюра графическим методом. Определение удельной поверхности адсорбента. Физический смысл const у-ния Ленгмюра. Амах- емкость монослоя, максимальная адсорбция, которая достигается при заполнении всех адсорбционных центров. К- const адсорбционного равновесия ( const скорости) К=qeQ/RT. Уравнение Ленгмюра является универсальным уравнением, тк оно описывает все 3 участка и его const имеют физический смысл, в отличие от уравнения Ьедевера-Фрейдлина( lgA=lgβ+1/nlgC). Г  рафический способ определения const уравнения Ленгмюра.Р/А 1/А=(1+КР)/(АмахКР) *Р Р/А=(1+КР)Р/АмахКР; Р/А=1/АмахК+Р/Амах α ctgα=Амах 1/АмахК Р 24. Адсорбция как обратимый экзотермический процесс. Интегральная и дифференци-альная теплота адсорбции. Δ  F↓ 0<ΔF=ΔH-TLS ΔS↓0 ΔH<0→+Q- самопроизвольная адсорбция, является экзотермическим процессом.qинт интегральная- кол-во тепла qдиф дифференциальная- кол-во тепла выдел адсорбции данного кол-ва выдел при дополнит адсорбции адсорбтива на 1 гр адсорбента малого кол-ва адсорбтива в qинт=Q/m (Дж/гр адсорбента) расчете на 1 моль адсорбтива qдиф=dQ/da (Дж/моль а-тива) а а Адсорбция<=>Десорбция, при ↑Т→↓А, а ↑Д, по принципу Ле-Шателье. 25. Сравнительная характеристика физической адсорбции и хемосорбции.
26. Кривые потенциальной энергии для физической адсорбции и хемосорбции. Адсорбция двухатомного газа на металле(х2) U-энергия межмолекулярного взаимодействия. 1-физическая адсорбция х2=х+х по 2 1 2-хемосорбция Θ=0 вер Qха(Θ80) хно сть Е ад r-расстояние от пов-ти сор  бен Qха(Θ0)та 27. Природа адсорбционных сил. Уравнение Леннарда-Джонса. Природа адсорбционных сил- физическая адсорбция происходит под действие межмолекулярных Ван-дер-Вальсовых сил. 1)ориентационные(полярный адсорбент-полярный адсорбтив) 2)дисперсионные( неполярный адсорбент-неполярный адсорбтив) 3)индукционные(неполярный адсорбент-полярный адсорбтив, полярный адсорбент-неполярный адсорбтив). Наиболее распространены дисперсионные силы, они имеют квантовую природу, проявляются между мгновенными диполями, возникают при сближении молекул за счет флуктуации электрической плотности. Uмежмол взаим=Uор+Uдисп+Uинд. Адсорбционные силы являются дальнодействующими и распространяются на расстояние 10-7м. энергия межмолекулярного дисперсионного притяжения:Uпр=-С/r6, «-» условный. Энергия борновского отталкивания: Uотт=В/r12. Энергия дисперсионного взаимодействия для одной молекулы U= С/r6+ В/r12- у-ние Леннарда-Джонса. Полная энергия взаимодействия: U= СΣ1/r6+ ВΣ1/r12-тк идет суммирование сил адсорбции силы являются дальнодействующими. И  зобара адсорбции.А Р=const 1 2 3 1-физическая адсорбция 2- переход от физической к хемосорбции 3-разложение адсорбционного комплекса. Т 28. Теория полимолекулярной адсорбции БЭТ, предпосылки теории. Уравнение изотермы адсорбции БЭТ, его анализ. БЭТ(Брунауэр, Эммет, Теллер). А 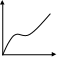 Предпосылки: 1)на поверхности адсорбента имеется определенное число активных центров 2)пренебрегаем взаимодействием между соседними молекулами в адсорбционном слое 3)каждая молекула1-ого слоя представляет собой возможный центр для адсорбции и образования 2-ого слоя 4)предполагается что все молекулы 2-ого и всех последующих слоев имеют такую же Σ статистических состояний, как в Р/Рs в жидком и отличаются от состояния 1-ого слоя. Авторы рассматривали адсорбцию как серию квазистатических реакций образования единичных комплекс. Молекула газа+активный центр→единичный комплекс; молекула газа+ единичный комплекс→двойной комплекс и тд. Q1>Q последующих слоев.  ; с=КРS- const полимолекулярной адсорбции. КL- const объемной конденсации. Уравнение БЭТ: PS-давление насыщенного пара, P/PS-относительное давление пара. 29. Линейная форма уравнения БЭТ. Нахождение констант уравнения БЭТ графическим методом. Определение удельной поверхности адсорбента. 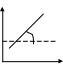переворачиваем и умножаем обе стороны у-ния на величину P/PS.  /(1-Р/РS)  P/PS/(A(1-P/PS) tgα=C-1/АмахС решая систему уравнений определяем Амах и С. Α Sуд=АмахS0Na P/PS 30. Кинетика адсорбции. Динамическое уравнение адсорбции. Уравнение Френкеля. Кинетические кривые адсорбции при разных температурах. Динамическое уравнение: А=nτ, n-число контактов молекул, τ-время установления адсорбционного равновесия, зависит от температуры и количества выделившегося тепла. Френкель: τ= τ0еQa/RT, τ0-const равная периоду колебаний атомов в решетке адсорбента τ0=10-13с. скорость адсорбции определяется скоростью диффузии адсорбтива к адсорбенту Кинетические кривые при разных температурах. 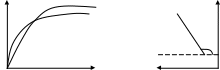 А Т1 ln(Aр-А τ) dA/d τ=K(Ap-Aτ) 1порядокТ2 -ln(Ap-Aτ)=Kτ+const Τ=0 Aτ=0 constинт=-lnAp T1 α τ τ |