|
|
Ответы к Колойдной химии экзамен, Мирэа тхт. Все лекции по колде. 1. Предмет коллоидной химии. Почему поверхностные явления и дисперсные системы изучают в рамках одной дисциплины коллоидной химии Значение коллоидной химии для технологии
52. Гетерогенная конденсация.
Гетерогенное образование новой фазы. Если в метастабильной фазе имеются какие-либо поверхности или какие-то посторонние включения, на которых с достаточной скоростью может происходить образование и рост зародышей, то в зависимости от их природы наиболее вероятное гетерогенное зародышеобразование- смачивание.
Работа гетерогенного зародышеобразования: Wкргет=f(Θ)Wкргом
Θ=0 f=0 Wкргет-мала; Θ=180 f=1 Wкргет= Wкргом .
Наличие поверхностей избирательного смачиваемых новой фазой в присутствии старой приводит к сильному уменьшению гетерогенной работы образования кристаллических зародышей.
53. Причины построения мицелл ионностабилизованных золей. Привести примеры.
Мицелла- отдельная частица дисперсной фазы ультрадисперсной системы с жидкой дисперсионной средой, состоящая из кристаллического или аморфного ядра и поверхностного слоя включающего сольватно связанные молекулы окружающей среды. Принципы построения мицелл: 1)агрегат мицеллы должен быть нерастворимым соединением 2)потенциалопределяющими ионами могут быть ионы образовывающие дисперсную фазу, изоаморфным им ионы и органические ионы с высокой адсорбционной способностью 3)противоионы образуют с потенциалопределяющими ионами растворимое соединение 4) мицеллы в целом электронейтральны. Строение мицеллы на примере сернистой сурьмы. 2SbCl2(изб)+3H2S=Sb2S3↓+6HCl

Cl- 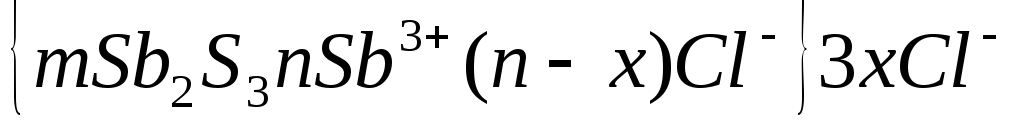
Cl- адсорбционный слой агрегат
Sb3+ Sb3+ ядро
Cl- Cl- Cl- Cl- мицела
Sb2S3 диффузный слой Типы потенциалопределяющих ионов:
Ионы одноименные с ионом агрегатом
Cl- Sb3+ Sb3+ Cl- 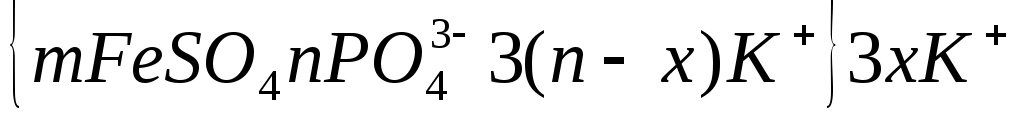
Cl- Ионы изоаморфные 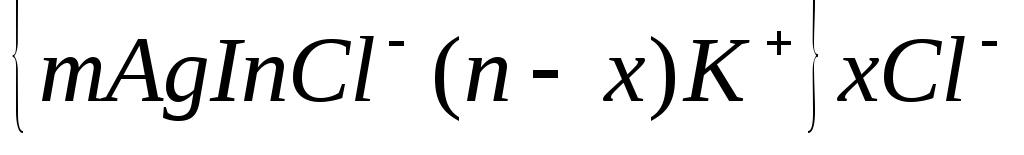
Ионы органические обладающие высокой адсорбционной способностью 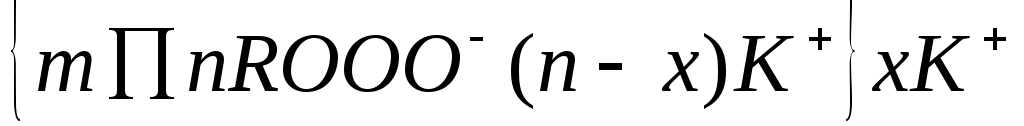
54. Пептизация как физико-химический метод получения коллоидных систем. Механизмы пептизации. Правило осадков Оствальда.
Пептизация- расщепление на первичные частицы под действием внешней среды агрегатов возникших в результате обратимой коагуляции дисперсных систем.
3 способа пептизации: 1)адсорбционная пептизация- отталкивание частиц осадка вызывающий двойной электрический слой(ДЭС), за счет ионов добавленного электролита стабилизатора 2)пептизация путем поверхностной диссоциации- связано с образованием ДЭС методом поверхностной диссоциации. Пептизатор вызывает образование растворимых соединений на поверхности частиц 3)пептизация путем промывания осадка- если на поверхности частиц в осадке есть ДЭС, но он сжат. Промывая удаляем избыток электролита- расширение ДЭС и получение золей.
П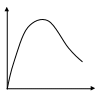 равило осадков Оствальда равило осадков Оствальда
количество При постоянном содержании пептизатора
растворившегося Спепт=const с возрастанием количества взятого для
осадка пептизации осадка количество осадка
перешедшего в раствор сначала
увеличивается, а затем уменьшается.
количество осадка
взятого для растворения
55. Получение лиофильных коллоидных систем путем самопроизвольного диспергирования. Вывод уравнения Ребиндера-Щукина.
Лиофильные системы образуются спонтанно, тк между веществом дисперсной фаза и дисперсной средой осуществляется интенсивное взаимодействие. Тк процесс самопроизвольный, он сопровождается уменьшением свободной энергии. 2 условия устойчивости двухфазной дисперсной системы: 1)достаточно низкое межфазное поверхностное натяжение 2)быстрый рост поверхностного натяжения с уменьшением радиуса частиц. Представители: коллоидные ПАВ и растворы высокомолекулярных соединений.
Вывод уравнения Ребиндера-Щукина. ΔF=ΔU+ΔS12σ12-TΔS при дроблении объем системы не меняется и ΔU=0. поверхность диспергирования увеличивается, те ΔS12>0
ΔS>0 ΔF≤0; ΔS12σ12<ТΔS; ΔS
na2; ТΔS
nγKT; na2σ12< nγKT; σкр= γKT/а2; а≈10-8м, σкр≈0,01 Дж/м2 σ12<σкр- самопроизвольное диспергирование.
56. Броуновское движение, его причины и общенаучное значение.
Колебания и перемещения частиц увеличиваются с уменьшением их размера и увеличением температуры. Причина: внутренние присущие самой системе факторы. Причина броуновского движения состоит в том, что молекулы окружающей среды(жидкости, газа) сталкиваются с частицами дисперсной фазы. В результате частица получает громадное число ударов. Если частица велика, то число этих ударов так велико, что вследствие статического закона импульсы взаимно компенсируются, и результирующий импульс равен о. если частица мала, то увеличивается вероятность того, что число или интенсивность ударов с одной стороны будет больше чем с другой. Результирующая сила вызовет смещение. Броуновское движение частицы указывает на тепловое движение среды. В броуновском движении участвуют частицы с размером менее 5*10-6м(5нм)
57. Соотношение между средне квадратичным сдвигом и коэффициентом диффузии. Вывод уравнения Эйншнеина-Смолуховского.
О сновной постулат: полная хаотичность движения частиц, те частица рассматривается как случайно блуждающая. Частица 1020 раз в секунду меняет свое направление. Истинный путь движения частицы определить не возможно, только средний. М сновной постулат: полная хаотичность движения частиц, те частица рассматривается как случайно блуждающая. Частица 1020 раз в секунду меняет свое направление. Истинный путь движения частицы определить не возможно, только средний. М
 С1 С2 С1 С2

Вывод уравнения. Уравнение Эйнштейна: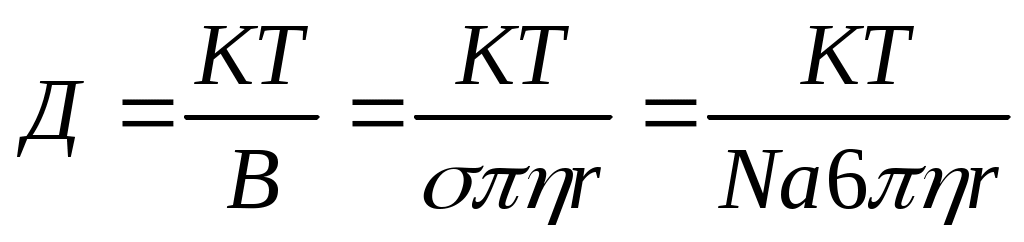 В-коэффициент трения по Стоксу. m1=1/2C1 В-коэффициент трения по Стоксу. m1=1/2C1 S m2=1/2C2 S m2=1/2C2 S; m=m1-m2=1/2(C1-C2) S; m=m1-m2=1/2(C1-C2)  S (C1-C2) / S (C1-C2) / =-dC/dX =-dC/dX
m=-1/2 2(dC/dX)S m=- Д(dC/dX)Sτ приравняем; 2(dC/dX)S m=- Д(dC/dX)Sτ приравняем;  =2Дτ-среднеквадратичный сдвиг; =2Дτ-среднеквадратичный сдвиг;  =√2Дτ =√2Дτ
58. Понятие о диффузии. Первый и второй законы Фика. Физический смысл коэффициента диффузии, его размерность.
Диффузия- самопроизвольный процесс переноса вещества, приводящий к выравниванию концентраций и химических потенциалов в результате теплового движения молекул, ионов частиц(из области больших концентраций в область меньших). Сопровождается увеличением энтропии. В однокомпонентной системе- самодиффузия.В многокомпонентной системе- взаимодиффузия.Выражения для идеальной диффузии 1 и 2 закон Фика. dm=-Д(dc/dx)Sdτ-1 закон (описывает стационарный процесс) m=- Д(dc/dx)Sτ (см2/с); дс/дτ=Д(д2С/дх2)-2 закон ( описывает нестационарный процесс. Те накопление вещества в различных точках пространства в зависимости от времени поглощения вещества тв телом, те описывает адсорбцию). Физический смысл коэффициента Д: масса вещества перенесенного через 1 площади за 1 времени, при gradC=1. Поток диффузии:ig=-Д(dC/dx). При переносе газа и компонента раствора в пористых телах различают 2 механизма: 1)диффузионный- вещество переносится в виде раствора 2)фазовый- вещество образует отдельную фазу и перенос происходит по парам и дефектам. Различают поток Кнуцена (при малых давлениях и при малых температурах , длина свободного пробега λ>>r, где r-диаметр пор; молекулы сталкиваются со стенками поры и сталкиваются друг с другом). Ламинарный поток Пуазеля(λ<кб молекулы проходят через поры не сталкиваясь со стенками, при увеличении диаметра пор проницаемость определяется истечением газов или растворов из отверстия.
59. Диффузионно-седиментационное равновесие. Вывод гипсометрического закона.
iд>iс 10-10м; iд≈iс 10-7-10-9м-ультрадисперсные частицы; iдс 10-6 и более м.
Вывод: iд=iс ; iд=-Д(dC/dX); ic=UC; mg=BU=>U=mg/B; -Д(dC/dX)=(mg/B)*C;
-Д(dC/dX)=(mgД/КТ)*C; КТ(dC/C)=mgdX- проинтегрируем С0 до Сn и h0 до hn; КТln(C0/Cn)=mgh=> Ch=C0e-(mgh/KT)-для концентраций; КТln(P0/Ph)=mgh- для давлений.
60. Седиментация в гравитационном поле. Вывод уравнения для определения радиуса частиц дисперсной фазы по скорости седиментации. Условия соблюдения закона Стокса. Седиментационное уравнение незаряженной частицы.
Закономерности седиментации в гравитационном поле: на каждую частицу действует сила тяжести(гравитационная сила) и подъемная сила Архимеда.Fд=mg=Vρg; Fа= Vρ0g;
Fсед=Fд-Fa=mотнg=V(ρ-ρ0)g; Fтр=BU=6πηrU; Fсед=Fтр; V(ρ-ρ0)g= 6πηrU; 4/3πr3(ρ-ρ0)g= 6πηrU;
U= 2r2(ρ-ρ0)g/9η; r=√(9ηU/2 (ρ-ρ0)g); Sсед-const седиментации Sсед=U/g=mотн/В=2r2(ρ-ρ0)/9η
 F(r) интегральная кривая- показывает F(r) дифференциальная кривая- F(r) интегральная кривая- показывает F(r) дифференциальная кривая-
весовое содержание частиц 1 показывает плотность распред по
Q данного или большего радиуса. массе частиц различного радиуса
2 1-монодисперсная система
2-полидисперсная система
F(r)=dФ(r)
r2 r 1 r rmin rmax
Условия соблюдения закона Стокса: 1)скорость оседания должна быть постоянна(0,1-100мкм) 2)частица должна иметь сферическую форму 3)частицы должны быть твердыми 4)частицы обязательно должны смачиваться жидкостью в которой мы проводим анализ 5)на оседание отдельной частицы не должны влиять соседние частицы(проводят седиментацию в разбавленных растворах) 6)оседание должно проходить в ламинарном режиме (0,1-100мкм).
Седиментационное уравнение незаряженной частицы: ρ- плотность жидкости, m0-масса жидкости в объеме частицы, 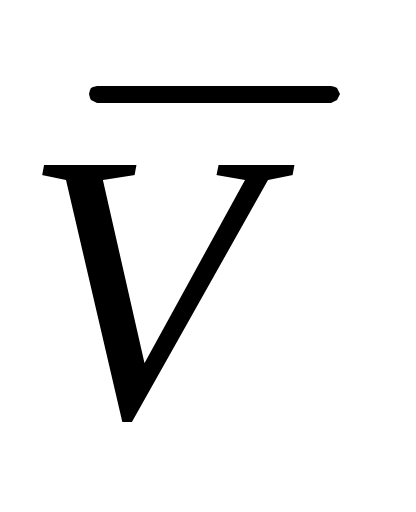 - удельный объем частицы. Fсед=mg-m0=m(1- - удельный объем частицы. Fсед=mg-m0=m(1-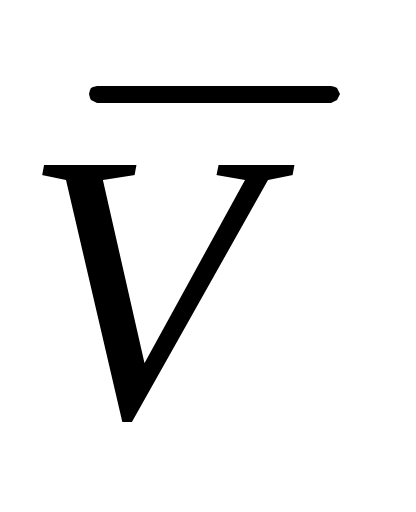 ρ)g; m(1- ρ)g; m(1-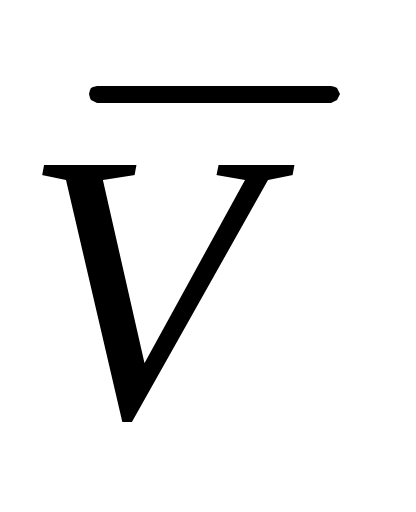 ρ)g=BU ρ)g=BU
61. Интегральные и дифференциальные кривые распределения частиц полидисперсных систем по размерам.
 F(r) интегральная кривая- показывает F(r) дифференциальная кривая- F(r) интегральная кривая- показывает F(r) дифференциальная кривая-
весовое содержание частиц 1 показывает плотность распред по
Q данного или большего радиуса. массе частиц различного радиуса
2 1-монодисперсная система
2-полидисперсная система
F(r)=dФ(r)
r2 r 1 r rmin rmax
62. Седиментация в центробежном поле. Определение массы частиц методом скоростного ультрацентрифугирования.
В ультрацентрифугах применяют мощное силовое поле. Ускорение 105g, а число оборотов до 75000 оборотов в минуту. U→dx/dt- под действием ω2x(угловая скорость вращения; зависит от оборотов) центробежного ускорения для осаждения частиц. B(dx/dt)= m(1-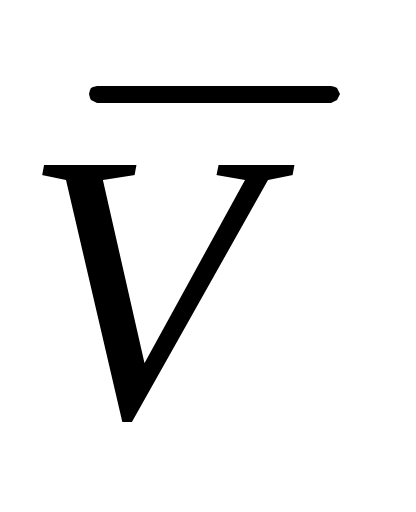 ρ) ω2x=>Д=КТ/В=> ρ) ω2x=>Д=КТ/В=>
В=КТ/Д=>КТ/Д(dx/dt)- m(1-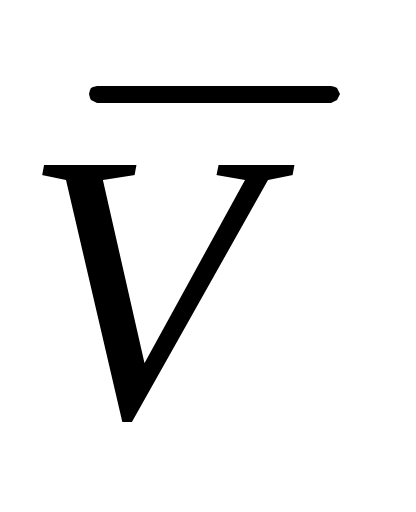 ρ) ω2x; КТ/Д= m(1- ρ) ω2x; КТ/Д= m(1-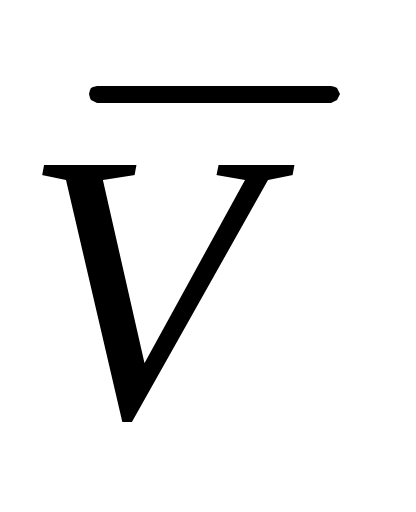 ρ) ω2x(dx/dt) Sсед= ω2x(dx/dt); S-Сведберг 1св=10-13с; m=KTS/Д (1- ρ) ω2x(dx/dt) Sсед= ω2x(dx/dt); S-Сведберг 1св=10-13с; m=KTS/Д (1-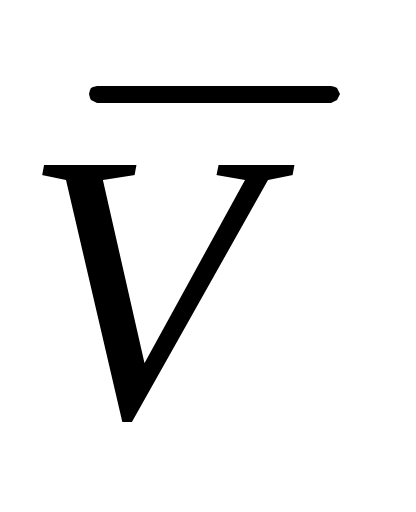 ρ)- метод является относительным, тк надо определить Д независимым методом. ρ)- метод является относительным, тк надо определить Д независимым методом.
63. Определение массы частиц методом равновесного ультрацентрифугирования.
-равенство потоков диффузорного и седиментационного, ускорение 103g. ic=cm(1-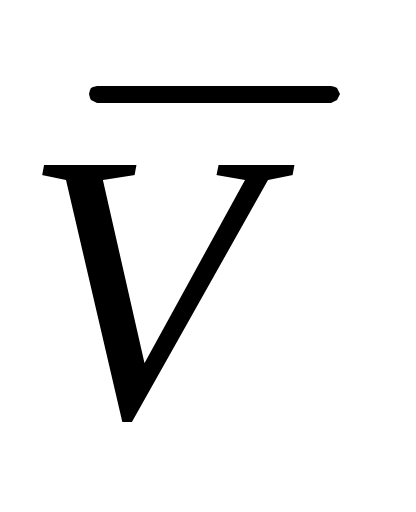 ρ) ω2x1/Bdτ; ρ) ω2x1/Bdτ;
Iд=Д(dC/dt) dτ; cm(1-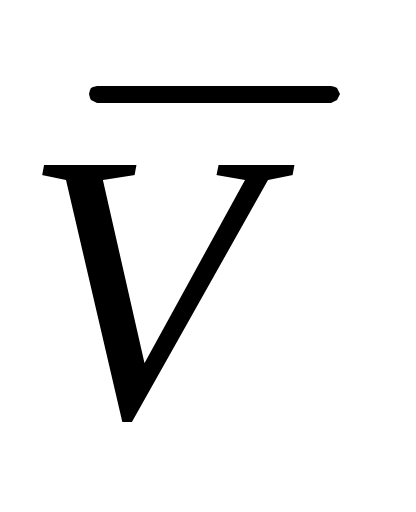 ρ) ω2x1/Bdτ= Д(dC/dt) dτ; cm(1- ρ) ω2x1/Bdτ= Д(dC/dt) dτ; cm(1-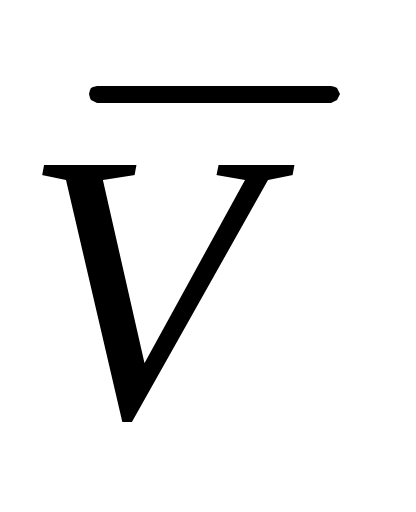 ρ) ω2x= КТ(dC/dх); ρ) ω2x= КТ(dC/dх);
cm(1-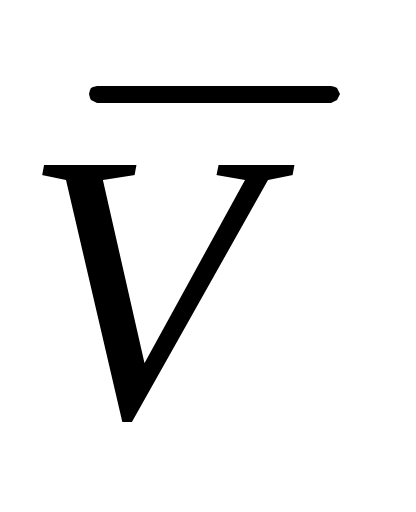 ρ) ω2xdх= КТ(dC/С)- интегрируем от х1 до х2 и от С1 до С2; ρ) ω2xdх= КТ(dC/С)- интегрируем от х1 до х2 и от С1 до С2;
m(1-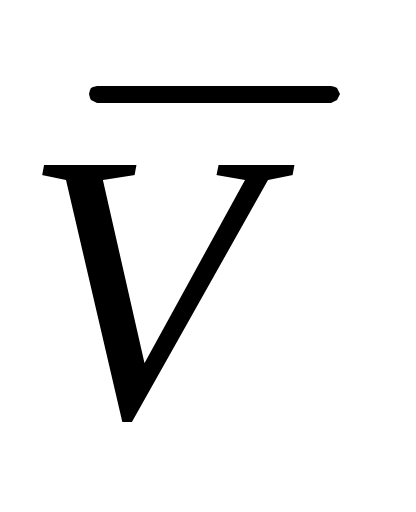 ρ)ω2 (x22-х12)/2=KTln(C2/C1); m= 2KTln(C2/C1)/ (1- ρ)ω2 (x22-х12)/2=KTln(C2/C1); m= 2KTln(C2/C1)/ (1- ρ)ω2 (x22-х12)- масса одной частицы. Абсолютный метод определения массы частиц и макромолекул. ρ)ω2 (x22-х12)- масса одной частицы. Абсолютный метод определения массы частиц и макромолекул.
64. Термодинамическая седиментационная устойчивость и факторы влияющие на нее.
ТСУ связано с равновесным ультрацентрифугированием. Мерой ТСУ является гипсометрическая высота hc. Те высота на которой концентрация дисперсной фазы частично уменьшается в е раз.
Hc=KT/mотнg=KT/V(ρ-ρ0)g-ТСУ не зависит от вязкости и увеличивается с повышением температуры, тк усиливается тепловое движение.
65. Кинетическая седиментационная устойчивость и факторы влияющие на нее.
- зависит от вязкости, плотности среды и размеров частиц. КСУ=1/Sсед=В/mотн=9η/2r2(ρ-ρ0).
66. Явления наблюдаемые при взаимодействии видимого света с веществом.
П  реобладание того или иного явления зависит от соотношения между размерами частицы(а) и длинной волны(λ). 1)прохождение света через среду без изменений своего I0 In направления а<<λ. I0=In-истинные растворы. n-const-для оптически однородной реобладание того или иного явления зависит от соотношения между размерами частицы(а) и длинной волны(λ). 1)прохождение света через среду без изменений своего I0 In направления а<<λ. I0=In-истинные растворы. n-const-для оптически однородной
среды.2)поглощение света(наблюдается окраска) I0>In (а<λ) 3)для грубодисперсных систем- отражение или преломление света(а>>λ) 4)рассеяние света(а≈0,1λ)- I0
преобразование светового пучка одного направления в световые пучки I0
разных направлений. В ультрадисперсных система и оптически неоднородных средах(n≠const).
67. Виды рэлеевского рассеяния света и его условия. Физическая сущность рассеяния света.
1)Рэлеевское- рассеяние мутными средами(ультрадисперсные системы) 2) Молекулярное- истинные растворы и газы, проходит за счет флуктуации плотности в газах и жидкостях и концентрированных растворах. Мутность в ультрадисперсных системах(эффект Тендаля) In/I0=e-τl, где τ-мутность. 2 условия рэлеевского рассеяния. Световая волна- переменное электромагнитное поле, оно индуцирует диполи в атомах или молекулах и возникают вторичные волны, таким образом падающие и рассеивающие волны разные. В оптически однородной среде диполи расположены хаотично и гасят друг друга во всех направлениях, кроме направления первичного пучка. В n≠const поглощение волны не происходит, те наблюдается рассеяние света.
68. Индикатрисы рассеяния поляризованного и неполяризованного света большими и малыми частями.
1. Рассеяние света малыми частицами (а=λ/20). Θ- угол наблюдения, φ-угол между подающей и рассеянной волной. 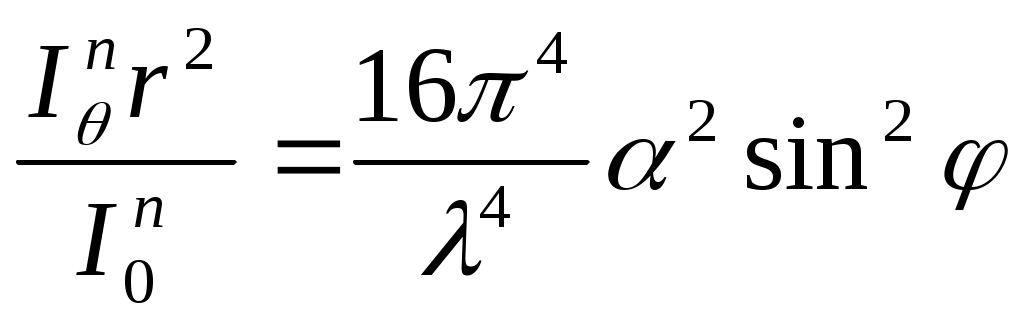 -для поляризованного света, I0n-приведенная интенсивность рассеяния. 2. Индикатриса рассеяния 1-проэкция угловой зависимости света(рассеянного) на плоскость чертежа 2-…на плоскость перпендикулярную чертежу 3-индикатриса неполяризованного рассеяния. -для поляризованного света, I0n-приведенная интенсивность рассеяния. 2. Индикатриса рассеяния 1-проэкция угловой зависимости света(рассеянного) на плоскость чертежа 2-…на плоскость перпендикулярную чертежу 3-индикатриса неполяризованного рассеяния. 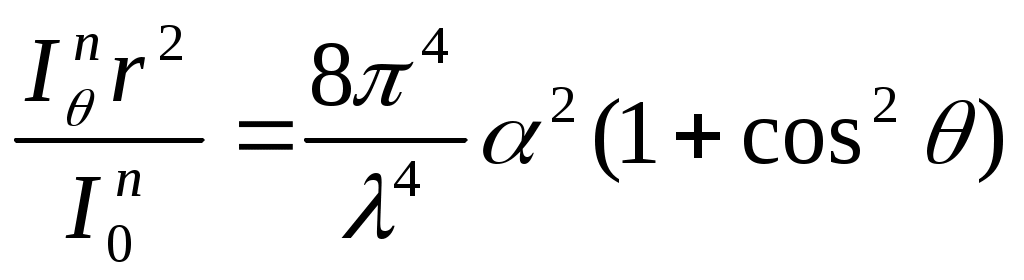 -для неполяризованного света. Поляризованный свет раскладывается на горизонтальную(3) и вертикальную(2) составляющие. 3. Рассеяние света большими частицами (а>λ/20) 1) возникает угловая ассиметрия; внутричастичная интерференция отсутствует 2)угловая зависимость интенсивности рассеяния света большой частицей. -для неполяризованного света. Поляризованный свет раскладывается на горизонтальную(3) и вертикальную(2) составляющие. 3. Рассеяние света большими частицами (а>λ/20) 1) возникает угловая ассиметрия; внутричастичная интерференция отсутствует 2)угловая зависимость интенсивности рассеяния света большой частицей.
1. 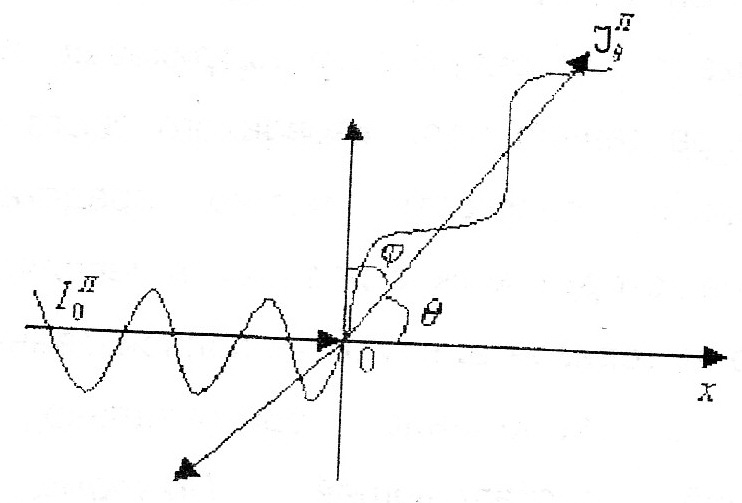 2 2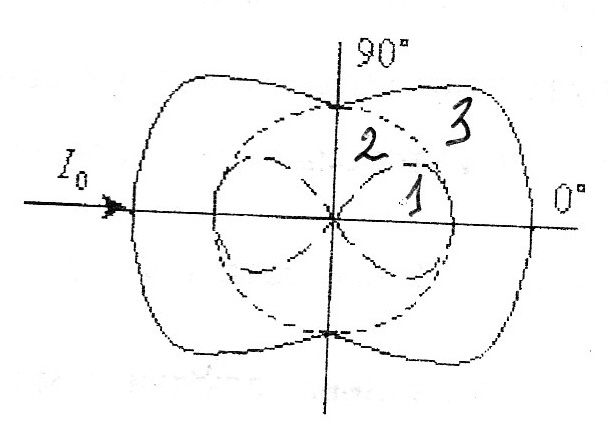
3.1) 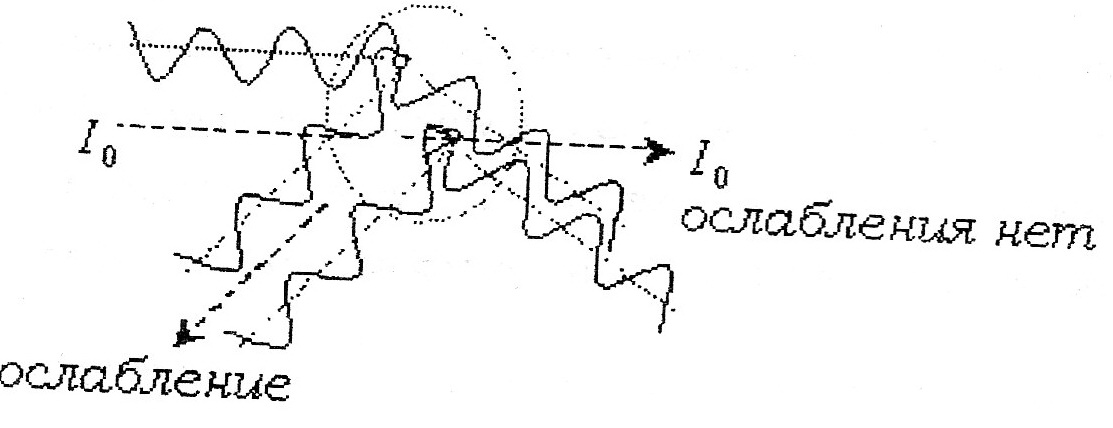 2) 2) 
|
|
|
 Скачать 2.71 Mb.
Скачать 2.71 Mb.
 равило осадков Оствальда
равило осадков Оствальда
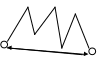 сновной постулат: полная хаотичность движения частиц, те частица рассматривается как случайно блуждающая. Частица 1020 раз в секунду меняет свое направление. Истинный путь движения частицы определить не возможно, только средний. М
сновной постулат: полная хаотичность движения частиц, те частица рассматривается как случайно блуждающая. Частица 1020 раз в секунду меняет свое направление. Истинный путь движения частицы определить не возможно, только средний. М
 F(r) интегральная кривая- показывает F(r) дифференциальная кривая-
F(r) интегральная кривая- показывает F(r) дифференциальная кривая- 
 реобладание того или иного явления зависит от соотношения между размерами частицы(а) и длинной волны(λ). 1)прохождение света через среду без изменений своего I0 In направления а<<λ. I0=In-истинные растворы. n-const-для оптически однородной
реобладание того или иного явления зависит от соотношения между размерами частицы(а) и длинной волны(λ). 1)прохождение света через среду без изменений своего I0 In направления а<<λ. I0=In-истинные растворы. n-const-для оптически однородной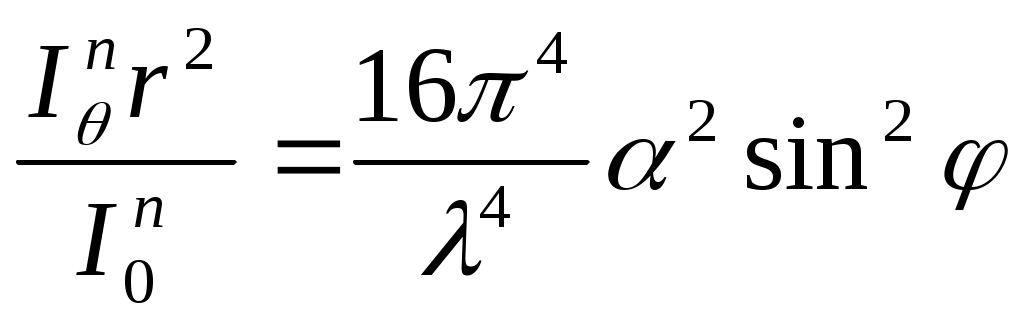 -для поляризованного света, I0n-приведенная интенсивность рассеяния. 2. Индикатриса рассеяния 1-проэкция угловой зависимости света(рассеянного) на плоскость чертежа 2-…на плоскость перпендикулярную чертежу 3-индикатриса неполяризованного рассеяния.
-для поляризованного света, I0n-приведенная интенсивность рассеяния. 2. Индикатриса рассеяния 1-проэкция угловой зависимости света(рассеянного) на плоскость чертежа 2-…на плоскость перпендикулярную чертежу 3-индикатриса неполяризованного рассеяния. 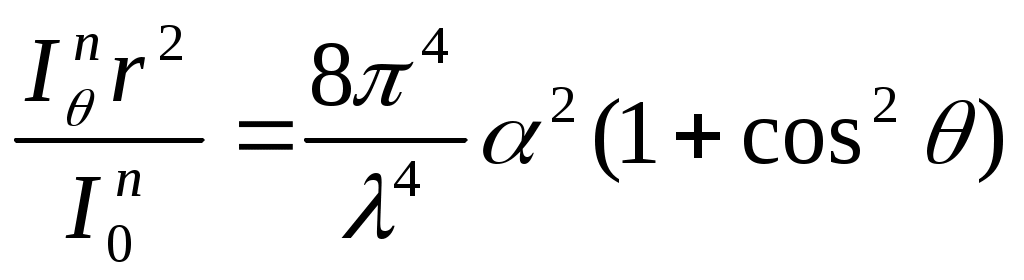 -для неполяризованного света. Поляризованный свет раскладывается на горизонтальную(3) и вертикальную(2) составляющие. 3. Рассеяние света большими частицами (а>λ/20) 1) возникает угловая ассиметрия; внутричастичная интерференция отсутствует 2)угловая зависимость интенсивности рассеяния света большой частицей.
-для неполяризованного света. Поляризованный свет раскладывается на горизонтальную(3) и вертикальную(2) составляющие. 3. Рассеяние света большими частицами (а>λ/20) 1) возникает угловая ассиметрия; внутричастичная интерференция отсутствует 2)угловая зависимость интенсивности рассеяния света большой частицей. 2
2
 2)
2)