Ответы к Колойдной химии экзамен, Мирэа тхт. Все лекции по колде. 1. Предмет коллоидной химии. Почему поверхностные явления и дисперсные системы изучают в рамках одной дисциплины коллоидной химии Значение коллоидной химии для технологии

• Название: 1. Предмет коллоидной химии. Почему поверхностные явления и дисперсные системы изучают в рамках одной дисциплины коллоидной химии Значение коллоидной химии для технологии
• Анкор: Ответы к Колойдной химии экзамен, Мирэа тхт
• Дата: 31.03.2022
• Размер: 2.71 Mb.
• Имя файла: Все лекции по колде.doc
• Тип: Документы; #430098
• страница: 5 из 7

69. Уравнение Рэлея, условия его применения анализ.

-справедливо для сферических частиц не проводящих электрического тока, малых по сравнению с длинной волны и в разбавленном растворе. 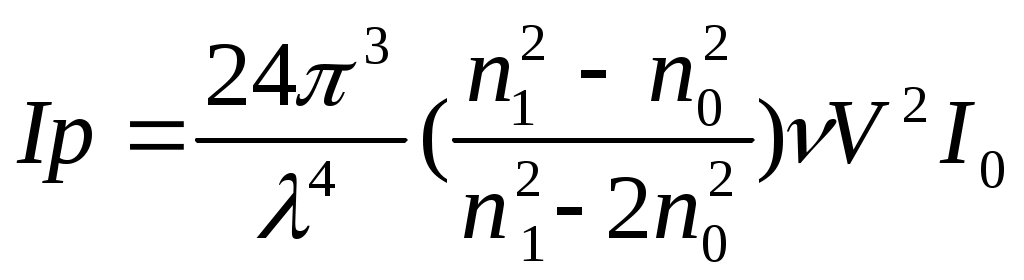, n₀,n₁-показатель преломления фазы и среды; V-объем частицы;υ-численная концентрация;λ- длинна волны. а≈0,1λ(40-70нм)

Ip Анализ уравнения Релея: 1)Ip=f(υ)-d разбавленном растворе можно

определить численную концентрацию 2)Ip=f(V²)=K υV²I₀, при С=const V↓Xраз

Ip=Kυx(V/x)²I₀=KυV²/xI₀ (в х раз) 3)Ip=f(1/λ⁴)-лучше рассеиваются короткие

волны(синие или голубые); проходящий свет обычно красный

4)Ip=f 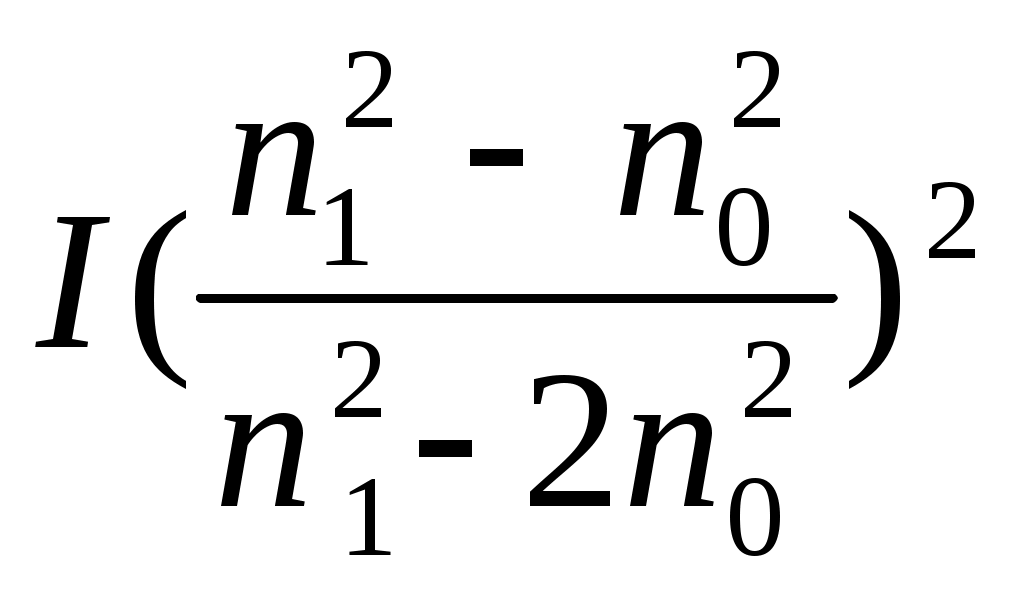, n₁=n₀-системы не рассеивающие свет(эмульсия)

10^-9 d,м

70.Оптические методы исследования дисперсных систем. Нефелометрия. Схема нефелометра. Определение размера коллоидных частиц методом нефелометрии.

Определение размера коллоидных частиц методом нефелометрии:

1) нефелометрический 2)турбодиметрический.

Нефелометрия основана на способности коллоидных систем

рассеивать свет. Нефелометрический метод основан на измерении

непосредственной интенсивности света рассеянного под некоторым

углом к падающему свету.

1-источник света 2,3-подвижные экраны 4,5- цилиндрические

кюветы 6,7-стеклянные цилиндрики 8,9-призмы 10-окуляр

Ip=KυV²I₀=KC_обVI₀; 1) с=const I₀KV’Ch’=I₀KV”Ch;

V’h’=V”h”=>V’=V”(h’/h”) 2)при известном размере частиц C’=C’(h’/h”)
71. Определение размера коллоидных частиц методом турбодиметрии.

-ослабление интенсивности света проходящей через дисперсную систему. Если принять рассеянный свет за фиктивно поглощенный, то можно получить соотношение:-dI=τIdx интегрируем от I₀ до I_n и от х=0 до х=l => ln(I₀/In)=τl; I_n=I₀e^-τl-связь мутности с оптической плотностью ln(I₀/In)=2.3lg (I₀/I_A)=2.3Д τ=2,3Д/l; 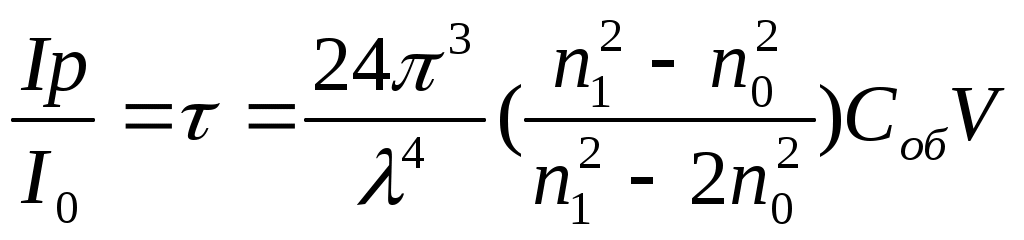; V=τ/С_обК

72. Микроскопия. Предел разрешения светового и электронного микроскопов. Формирование изображения в световом и электронном микроскопе.

С ветовая микроскопия. Каждый микроскоп характеризуется пределом разрешения(определяется количеством оптики и длинной волны света, качество оптики зависит от опертурного угла(α)

Предел разрешения в вакууме: угловая апертура δ=λ/2sin α ; численная апертура δ=λ/2nsinα

Контрастность изображения формируется за счет поглощения света.δсв мк=2*10^-7м α

Увидеть ультрадисперсные частицы нельзя. Микроскопия характеризуется полезным увеличением микроскопа(М): М=δ_г/δ_м=2*10^-4/2*10^-7=10³

Электронная микроскопия- используется поток электронов, он отклоняется электрическим и магнитным полем, в него можно увидеть ультрадисперсные системы. Изображение формируется за счет электронного пучка. λ=h/mV если 50кВ, λ=10^-12м Предел разрешения:δ=2,5*10^-12м ведут наблюдение под углом 0,02 рад, λ=4*10^-10м=>δ=2*10^-10м δ_св/δ_эл=10^-7м/10^-10=10³.

Формирование изображения в электрическом микроскопе.

е е₁-упругое соударение атомов и вещества, е₂-неупругое соударение е- вторичное

рассеивание. В формировании изображения принимает участие е рассеянные

вследствие упругого соударения. Количество соударений е с атомами объекта зависит

от толщины объекта, его плотности и от химической природы элемента.
73. Принцип темнопольной микроскопии. Щелевой ультрамикроскоп, конденсор темного поля. Определение численной концентрации и размера коллоидных частиц.

Принцип темнопольной микроскопии лежит в основе ультрамикроскопии. Ультрамикроскопия использует видимый свет, но наблюдения ведут в рассеянном свете, нельзя непосредственно наблюдать частицу, можно обнаружить присутствие и подсчитать число частиц. Щелевой микроскоп(образец освещается сбоку интенсивным пучком света от дуговой лампы). Если образец однороден, о в микроскопе будет темное поле. Коллоидный размер виден в виде светлых точек на темном поле. Конденсатор темного поля является оптическим устройством для получения пустотелого конического пучка света. Световой пучок блокирован круглым экраном, который предотвращает попадание прямого пучка в объектив. Позволяет изучать броуновское движение, сегментационное равновесие и позволяет определять среднечисленные размеры частиц путем их подсчета при известных концентрациях дисперсной фазы, ассиметрию, полидисперсность. V=e²h υ=n/V, n- среднее число частиц. Сферическая частица: Vρ υ=C, C-световая концентрация. V=С/ρυ=>4πr³/3=Cρυ; 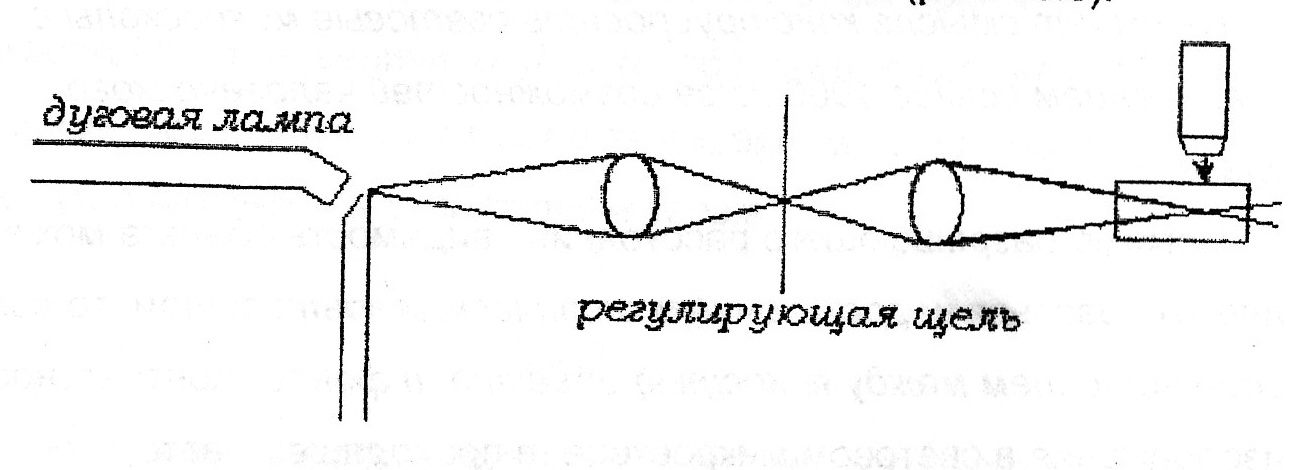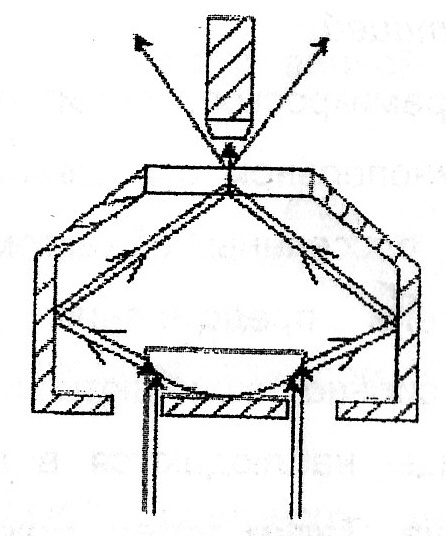. Условия которые необходимо соблюдать: 1)золь должен быть разбавлен 2)частица должны иметь определенный размер 3)коэффициенты преломления дисперсной фазы и дисперсионной среды должны сильно отличаться друг от друга. В ультрамикроскоп наблюдают лиофобные дисперсные системы.



74. Поглощение света дисперсными системами. Уравнение Бугера-Ламберта-Бера для истинных растворов. Чему равны оптическая плотность, мутность и светопропускание растворов?

Inp=I₀e^-εcl- для истинных растворов; ln(I₀/Iпр)=2.3lg(I₀/I_n)=εCl; lg(I₀/I_n)=Д-оптическая плотность; светопропускание-Т=(Iпр/I₀)100%/

75. Фиктивная абсорбция света в коллоидных системах.

-поглощение света в коллоидных и ультрадисперсных системах(обязательно рассеяние света).

Фиктивная абсорбция света для золей: Iпр=I₀e^-(K+ε)Cl

76. Причины и механизмы возникновения заряда на поверхности частиц.

Причиной является возникновение соприкасающихся фаз, благодаря избытку поверхностной энергии. Стремление к уменьшению свободной энергии вызовет определенную ориентацию молекул, ионов и е в поверхностном слое вследствие чего произойдет пространственное разделение зарядов и возникновение ДЭС. Механизмы возникновения: 1)эмиссия е с поверхности Ме( Ме→Ме⁺+е) 2)за счет поверхностных диссоциаций молекул (а)SiO₂+H₂O→H₂SiO₃ (песок) б) AgI ПИ:Ag⁺ ПО:I ^-) 3)в результате адсорбции( образование ионностабилизированных мицелл

( а) б) ) 4)если вещества составляющие фазы системы не способны обмениваться зарядами, то ДЭС образовывается благодаря ориентации полярных молекул( трибоэлектрический эффект- эбонитовая палочка) (FePO₄, NaHPO₄, Fe(NO₃)₃) Пример:

77. Связь электрического потенциала с поверхностным натяжением. Вывод уравнения Липмана, его анализ.

В ывод основан на том, что поверхность раздела фаз- это плоский конденсатор; при увеличении поверхности на dS заряд увеличивается на dq. dF^S=σdS+φdq(1) T=const интегрируем (1) F^S=σS+φq(2) дифференцируем (2) dF^S=σdS+Sdσ+φdq+qdφ(3) приравниваем (1) и (3) Sdσ+qdφ=0; dσ/dφ=-q/S=-q уравнение Липмана. Анализ: если знак потенциала и заряда совпадает, то при увеличении заряда на поверхности происходит уменьшение поверхностного натяжения, а система становится более устойчивой.

Полная плотность заряда: q^S=ZFГ=ZcNaГ.

78. Электрокинетические явления, их классификация по причинно-следственной связи и по объектам исследования.

Электроосмос- явление перемещения жидкости в капилляре под действие электрического тока.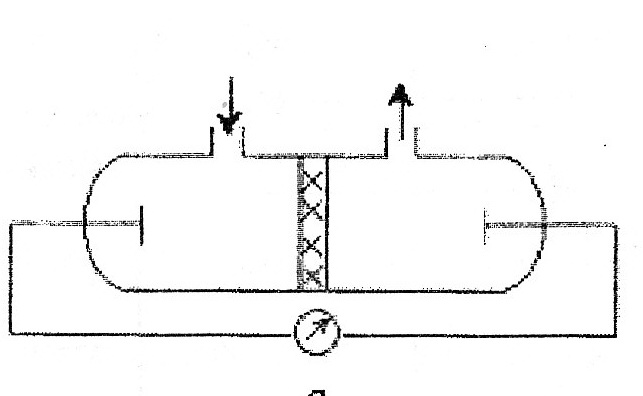

Жидкость движется к -. Обратное явление осмоса потенциал течение, те

явление возникновения разности потенциалов при прокачке жидкости через

пористые тела или мембраны.
Э 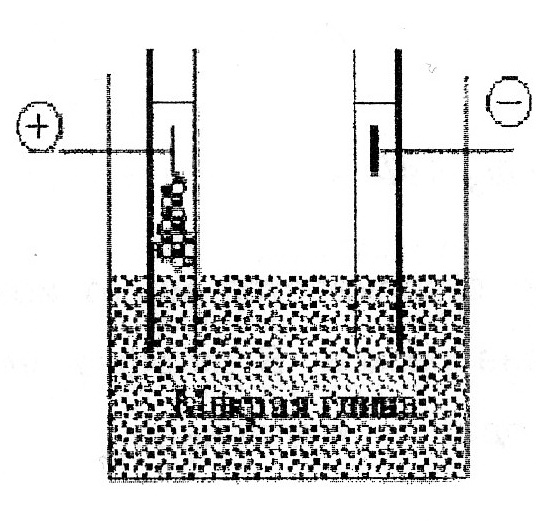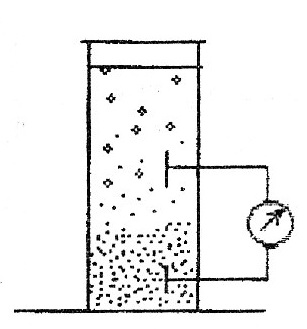лектрофорез-явление перемещения частиц дисперсной фазы во внешнем электрическом поле.

Если движущиеся частицы малы, то это ионная проводимость.

Обратный ему процесс- потенциал оседания(седиментация)-явление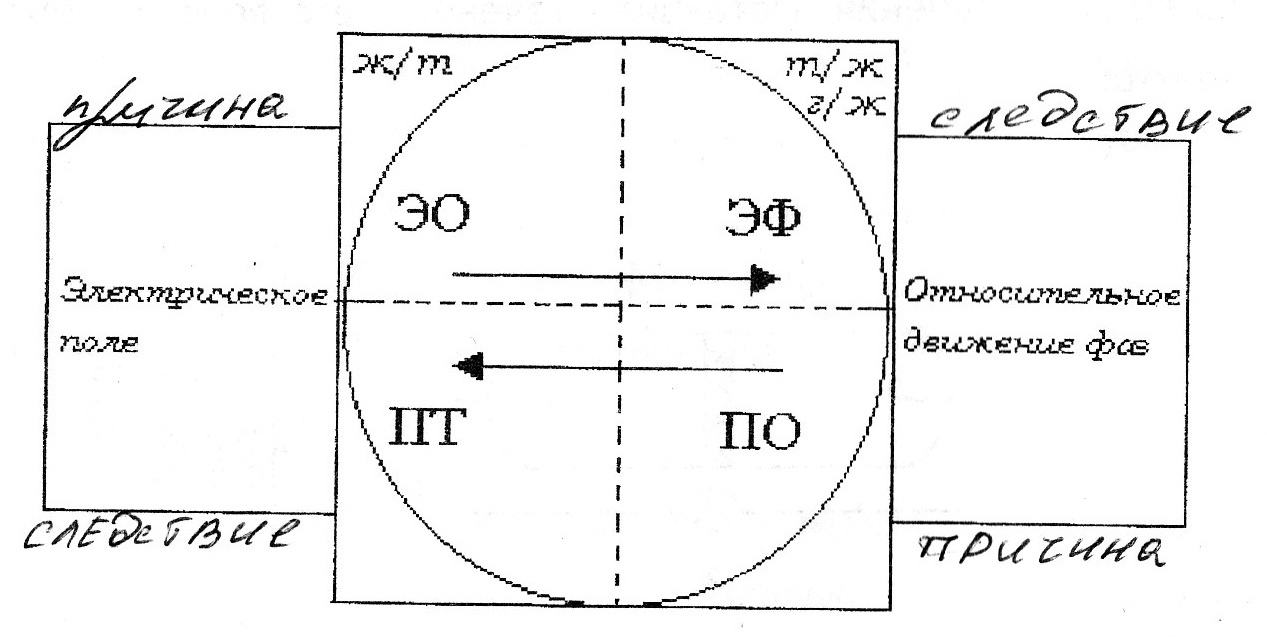

возникновения разности потенциалов.
Классификация:
7 9. Строение двойного электрического слоя(ДЭС). Количественная модель Гуи-Чепмена.

1. Теория Гельмгольца-Перена. ДЭС кА плоский конденсатор. φ₀ - +

Q^S=(ε_a/ δ) φ₀-(εε₀/δ)φ₀ - +

2. Теория Гуи-Чепмена. В реальных условиях распределение δ

на границе раздела фаз определяется соотношением сил электростатического притяжения ионов и теплового движения ионов(стремящихся к равномерному распределению). Тепловое движение ионов ДЭС- диффузное(размытое)строение. Модель основана на: 1)поверхность представляет собой однородно заряженную поверхность неопределенных размеров. 2) ионы диффузионной части представляют собой точечные заряды, которые подходят к поверхности сколь угодно близко. Распределение ионов в пространстве по закону Больцмана.3)работа переноса иона из объема в ДЭС имеет электростатический характер 4) растворитель влияет на ДЭС по средствам диэлектрической постоянной, которая будет одинакова по всему объему диффузионной части. Теория основана на подвижности ионов. ДЭС может достигать до 10^-4м

конц ПИ падает С С+ уравнение для концентрации ионов:

- + Сх=С_∞е^-Wx/RT= С_∞е^{-ZГφ /RT}

- + + X С_∞- концентрация ионов в растворе

- + + + φ_x- потенциал на расстоянии x от границы

- + + + + + С- раздела фаз.

80. Модель Штерна(внутренняя часть ДЭС).

1. поскольку ион имеет конечные размеры, то центр иона может приблизится к поверхности только в пределах радиуса гидратированного иона.2. в близлежащем слое учитывается потенциал Ф, который имеет некулоновскую природу.

- + φ₀ ДЭС-состоит из 2-х слоев( адсорбционного и диффузионного

- +++ слоя). U=ZFφ_б+Ф

- + +++ +

- ++++++ +++++++++

- ++++++++ +++++++++ х


81. Влияние электролитов на ДЭС. Зависимость толщины ДЭС и электрокинетического потенциала от концентрации и природы противоионов индеферентного электролита мицеллы. Изоэлектрическая точка, перезарядка.

Индеферентными называются электролиты не имеющие ионов способных достраивать кристаллическую решетку , адсорбироваться на поверхности и изменять величину потенциала поверхности φ₀. Преимущественно на ДЭС оказывает влияние ион электролита имеющий одинаковый заряд с противоионом мицеллы. При добавлении электролита происходит сжатие ДЭС. 1) Влияние концентраций электролита ;

2)влияние валентного электролита 3)влияние радиуса иона (Li⁺, Na⁺, Cs⁺) в лиотропных рядах ионов с увеличением радиуса иона увеличивается их адсорбционная способность, тк ион с большим радиусом менее гидратирован и более поляризован 4) влияние многовалентных ионов Th(No₃)₄ Частичная перезарядка вызывается многовалентными ионами противоположенными по знаку потенциал определяющим ионам (3⁺ 4⁺ заряды)

1) Изоэлектрическая точка возникает при полной помперсации заряда поверхности

2) 0-падение потенциала в исходной

Мицелле

1-KNO₃ 2-Ca(NO₃)₂ 3-Al(NO₃)₃

3) 4)

1 LiNO₃



2 NaNO₃

3 CsNO₃

82. Действие неиндеферентного электролита на ДЭС.

Неиндеферентные- не безразличные электролиты, содержащие ионы способные достраивать кристаллическую решетку поверхности и поэтому влияют на потенциал поверхности, а также на толщину ДЭС и на потенциал. 1 добавление электролит содержащих ионов с одноименными с потенциал определяющим ионом. 2 электролит который содержит ион противоположный по знаку потенциал определяющему.

1 при добавлении КF ζ

φ₀^’ 2 при добавлении еще большего

кол-ва КF, вступ в действие К

1. 
   котор будет сжимать
   

2 ДЭС, как индеферен

0. 
   тный ион
   

х С

83. Влияние разбавления, температуры и неиндеферентного электролита на ДЭС.

φ ζ С₁>С₂>С₃- разбавление золя

φ₀^’ Т₁<Т₂<Т₃

2

1

3-срыв потенциал ионов с-мы

х С,Т

84. Вывод формулы Гельмгольца-Смолуховского для определения величины электрокинетического потенциала по данным электроосмоса или электрофореза.

Э то уравнение устанавливает связь между скоростью электрокинетических явлений (U) и параметрами дисперсной среды(η, ε, ζ, Е). уравнение выводится на примере электроосмоса, в основе лежат следующие допущения: 1)толщина ДЭС значительно меньше радиусов пор и капилляров в тв фазе 2)слой жидкости непосредственно прилегающий к твердой фазе неподвижен 3)движение жидкости в порах тв фазы- ламинарное 4)распределение зарядов в ДЭС не зависит от приложенной разности потенциалов 5)тв фаза является диэлекстриком, а жидкость проводит электрический ток.

φ выражение для электрической силы которая действует на слой dx

φ₀ U(x) dFэл=Еfq=Eρdx=-Eε₀ε d²φ/dx²dx ρ-объемная плотность заряда

d²φ/dx²=-ρ/ε_абс=-ρ/ε₀ ε Fтр=η(dU/dx)=>dFтр=η d²U/dx²

dFэл=dFтр d²U/dx²=-Eε₀ε d²φ/dx² интегрируем х=l x=∞, φ=ζ φ_∞=0, U=0

U∞=0; (dφ/dx)_∞=0 (dU/dx)_∞=0 U=Eε₀εζ/η- скорость электроосмоса

δ φ(х) ζ=ηU₀/ε0εE=ηUэф/ε₀ε; U₀/E- электрофоретическая подвижность.

l dx

85. Агрегативная и седиментационная устойчивость коллоидных систем. Стабилизаторы, и их роль в придании коллоидной системе временной агрегативной устойчивости.

Седиментационная устойчивость- способность системы сохранять равномерное распределение частиц. Агрегативная устойчивость- способность системы сохранять размеры своих агрегатов или свою дисперсность. Агрегативная устойчивость рассматривается с 2-х точек зрения 1) термодинамической(а)термодинамически устойчивые- лиофильные б) термодинамически неустойчивые- лиофобные) 2)кинетической( лиофобные). Лиофобным системам придают кинетическую устойчивость путем введения стабилизатора. Лиофобные системы не устойчивы, тк они имеют избыток поверхностной энергии dF>0. dF^S=σdS. Если в системе нет стабилизатора, то система стремится уменьшить поверхностную энергию и будет происходить коагуляция(слипание частиц в дисперсной и ультрадисперсной системах с образованием более крупных агрегатов. 2 системы коагуляции: 1) коагуляция с фазовым контактом между частицами 2)коагуляционный контакт- поверхностное натяжение уменьшается и уменьшается свободная энергия.