Ответы к Колойдной химии экзамен, Мирэа тхт. Все лекции по колде. 1. Предмет коллоидной химии. Почему поверхностные явления и дисперсные системы изучают в рамках одной дисциплины коллоидной химии Значение коллоидной химии для технологии

• Название: 1. Предмет коллоидной химии. Почему поверхностные явления и дисперсные системы изучают в рамках одной дисциплины коллоидной химии Значение коллоидной химии для технологии
• Анкор: Ответы к Колойдной химии экзамен, Мирэа тхт
• Дата: 31.03.2022
• Размер: 2.71 Mb.
• Имя файла: Все лекции по колде.doc
• Тип: Документы; #430098
• страница: 6 из 7

86. Факторы устойчивости коллоидных систем.

Кинетическая устойчивость лиофобных дисперсных систем обеспечивается стабилизаторами( электролиты и ВМС). Факторы устойчивости: 1)термодинамический- обеспечивается при сохранении размера поверхности и поверхностного натяжения; снижается эффективность соударения между частицами и создаются потенциальные барьеры замедляющие или исключающие процесс коагуляции(слипания) 2)кинетический- снижает скорость коагуляции, связаны с гидродинамическими свойствами среды, связаны с замедлением сближения частиц, вытекание и разрушение прослоек среды. К термодинамическим фактору относятся: 1)электростатический фактор- уменьшение межфазного поверхностного натяжения при возникновении ДЭС на поверхности частиц в соответствии с уравнением Липмана( стабилизатор-электролит) 2)адсорбционно-сольватный- уменьшение межфазного поверхностного натяжения при взаимодействии частиц дисперсной фазы с дисперсионной средой благодаря адсорбции и сольватации 3)энтропийный- имеет две трактовки:-стремление частиц дисперсной фазы равномерно распределится по всему объему системы;- стабилизатор ВМС и неионогенный ПАВ.

К кинетическому фактору относятся: 1)структурно-механический фактор(стабилизатор ВМС)- действие фактора обусловлено тем, что на поверхности частиц образуются пленки ВМС, обладающих упругостью и механической прочностью, разрушение которых требует затраты энергии 2)гидродинамический- снижает скорость коагуляции из-за изменения вязкости среды и плотности дисперсионной фазы и дисперсионной среды 3)смешанный – характерен для реальных дисперсных систем совокупность термодин и кинетич факторов

87. Устойчивость и коагуляция лиофобных дисперсных систем по теории ДЛФО. Природа сил притяжения и отталкивания между частицами. Изменение этих сил с расстоянием. Потенциальные кривые, энергетический барьер, ближняя и дальняя агрегация.

В дисперсионной среде одновременно действуют силы притяжения и силы отталкивания. Силы притяжения имеют 1 природу, межмолекулярные Ван-дер-Вальсовы силы. Силы отталкивания зависят от природы стабилизатора. Теория ДЛФО- учитывает баланс сил притяжения и сил отталкивания. Рассматривает взаимодействие 2-х крупных частиц, для которых пренебрегаем тепловым движением, толщиной ДЭС. Общая энергия взаимодействия между 2-мя частицами: U=U_прит+U_отт/ силы притяжения действующие с дисперсной среде- дисперсионные силы притяжения, обусловлены квантовомеханическим эффектом. Особенностью дисперсионных сил является их дальнодействие обусловленное некоторыми причинами: 1)адитивностью 2)дисперсионные силы синхронны 3)характерен эффект электромагнитного запаздывания(электромагнитные волны>100нм не совпадают по фазе) Uпр(h)=-A/12πhⁿ n=1-3

F 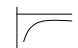-const Гомакера, учитывает природу взаимодействия тел, выражается в 1 энергии А=f(n,h)

-для 2 пластин: Uприт(h)=А/12πh²; - для сферических частиц Uприт(h)=Аr/12h

Силы отталкивания- учитывают электростатические факторы устойчивости h

Происходит при перекрывании двух ДЭС. Ели расстояние между частицами

велико, то φ падает до 0, если частицы перекрываются то φ не падает до 0 Uпр

Uотт Uотт(h)=Kφe^{-каппа h} Uотт 1 преобладание силы притяжения

1 2 быстрая коагуляция

2 3 3 медленная коагуляция

h

88. Зависимость скорости коагуляции от концентрации электролита, быстрая и медленная коагуляция.

Различают явную и скрытую коагуляцию. Быстрая коагуляция- коагуляция которая не зависит от электролитов. Медленная коагуляция- только наиболее вероятное слипание частиц приводит к коагуляции.

Uк Uотт 1- преобладают силы притяжения(10нм) h→0. быстрая

1 коагуляция(необратимая)образуется с контактом фаз

2 3 2-максимальные силы отталкивания h(10-100нм)

3 h>100нм, преобладают силы

Uпр притяжения(обратимая коагуляция)

С_м с_б с_эл-та

89. Кривые потенциальной энергии для систем с различной степенью агрегативной устойчивости.

U 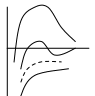отт 1 Umax- вероятность слипания частиц

1) Umax>>KT KT-энергия теплового движения

2) Umax<
ε=число слипаний/число столкновений=1

3 h 3) Umax≈KT -медленная коагуляция

4) Umax=Uприт -порог роагуляции

4

2

90. Кинетика коагуляции по Смолуховскому. Вывод уравнения для концентрации частиц через время коагуляции τ. Константы скорости быстрой и медленной коагуляции.

- рассматривает кинетическую коагуляцию для дисперсного золя со сферическими частицами, сталкивающимися в результате броуновского движения. Критическое расстояние взаимодействия=∑ радиусов частиц/их непосредственный контакт. Коагуляция происходит только при взаимодействии 2-х частиц. Коагуляция происходит как бимолекулярная химическая реакция. -dυ_∑/dτ=Kυ_∑²; К=8ДπR интегрирует и разделим переменные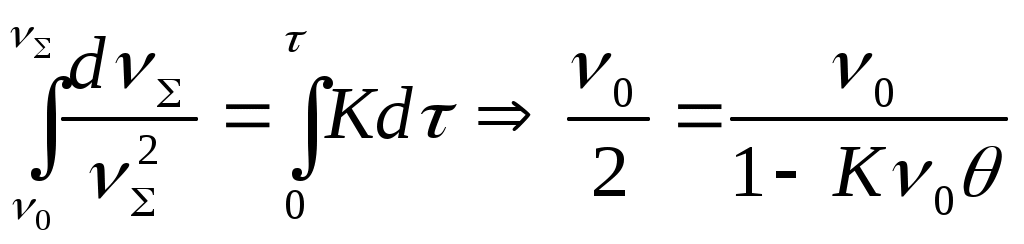

Θ -время половинной коагуляции. -изменение числа частиц со временем. При быстрой коагуляции θ=const

υ/ υ₀ К_б-const быстрой коагуляции

К_б=Кт=8πДR=8πК_бТ2r/6πηr=8K_бТ/3η. Для быстрой коагуляции ΔU=0 P=1.

υ_∑ Для медленной коагуляции ΔU≠0 Р≠0 Км=К_бРexp(-ΔU/К_бТ)

0,5 υ₀

υ₃

υ₂ τ∕θ

91. Правила коагуляции электролитами с точки зрения строения ДЭС.

1)коагуляцию вызывают любые электролиты, даже избыток стабилизатора 2)наиболее сильным коагуляционным действием обладает ион, заряд которого одинаков с зарядом противоиона 3)коагуляция наступает не мгновенно, а при добавлении минимального количества электролита- порог коагуляции(8 моль/л) 4)порог коагуляции тем меньше чем больше валентность иона. Правило Шульце-Гарди: валентность 1,2,3 порог коагуляции 1,20,50. правило Дерягина-Ландау: γ=K/Zⁿ n=6 1:64:729 1:2:3 5)порог коагуляции уменьшается с увеличением радиуса иона 6) коагуляция наступает при ζ=25 мВт

92. Концентрационная и нейтрализационная коагуляция.

Нейтрализационная коагуляция характерна для систем с частицами, обладающими малым электрическим потенциалом. На нейтрализационной коагуляции особенно сказывается специфическая адсорбция ионов добавляемого электролита, имеющих заряд, одинаковый по знаку с зарядом противоионов двойного электрического слоя. Эти ионы находясь в адсорбционном слое, резко снижают потенциал φ_б- происходит нейтрализация φ₀-потенциала уже в адсорбционном слое, так как при специфической адсорбции возможна перезарядка частиц, то для нейтрализационной коагуляции характерна область агрегативной неустойчивости между минимальной и максимальной концентрацией электролита. Приведении электролита в количестве, превышающем некоторое максимальное значение, дисперсная система может перейти во вторую область устойчивости, в которой частицы будут иметь заряд, противоположный заряду частиц в первой области устойчивости. Концентрационная коагуляция обусловлена сжатием ДЭС в результате увеличения ионной силы раствора. Этот вид коагуляции осуществляется при добавлении индеферентных электролитов, не способных к специфической адсорбции на поверхности коагулирующих частиц. Хотя при концентрационной коагуляции увеличивается количество противоионов в адсорбционном слое, однако эффект снижения потенциала в нем не является решающим. Преобладающее влияние ионной силы дисперсионной среды характерно для систем с высокозаряженными частицами.

93. Расклинивающее давление, его компоненты.

-возникает при сильном уменьшении толщины пленки в результате перекрывания или взаимодействия поверхностных слоев. Пленка- тонкая часть системы находящаяся между 2 межфазными поверхностями. 1)Толстая пленка h=2δ=>P₁=P₀ h=поверхностный слой, Р₀-давление в окр среде, Р₁-межфазовае давление,δ- толщина слоя. π(h)=0- расклинивающее давление.

2) При сближении пластин до перекрывания поверхностных слоев образуется тонкая пленка h<2δ=> π(h )=P₁-P₀. Изменение dG если в системе есть расклинивающее давление: dG=-SdT(σ₁₂+σ₂₃)dS+∑μ_in_i+(дG/dh)dh; π(h)= P₁-P₀=-1/S(дG/dh)_{T, ni, S}. π(h)- разность гидростатических давлений в пленке и окружающей пленку фазе, или приращение энергии Г. π(h)-является суммарным параметром, который учитывает как силы отталкивания, так и силы притяжения в дисперсионной среде. + силы отталкивания(молекулы втекают в прослойку); - силы притяжения(молекулы вытекают из прослойки). π(h) обусловлено различными компонентами: - Ван-дер-Вальсовы силы притяжения; + силы отталкивания(все факторы устойчивости)

94. Идеальные модели реологии. Модели Гука, Ньютона, Сен-Венана-Кулона.

Идеально упругое тело Гука представляется

в виде пружины с модулем Е. Р=Еγ –

деформация в пружине пропорциональна

напряжению. Особенность: полная механическая

и термодинамическая обратимость.

tg α = Е – модуль упругости (Юнга)





Идеально вязкое тело Ньютона: линейная

зависимость между напряжением сдвига (Р) и

скоростью деформации (γ). Перфорированный

поршень в вязкой среде. Коэф-т

пропорциональности называется вязкостью [Па · с]

или [Н · с/м²]. Полностью механически и

термодинамически необратимо.

tg α = η – вязкость (сопротивление с-мы

течению)

β – текучесть с-мы (диссипативная система)

Идеально пластическое тело Сен-Венана-Кулона.

Отсутствует пропорциональность между воздействием и

деформацией. Диссипативная с-ма, т.е. затраченная энергия

переходит в теплоту.

РT γ=0 γ=0 - деформация отсутствует

P>P_T γ>0 γ>0 - деформация происходит беспредельно

с любой скоростью. (Р_Т - предел текучести)

95. Принципы моделирования реологических свойств. Модель упругого тела Максвелла, Вывод уравнения, являющегося его математической моделью.

При последовательном соединении элементов, напряжения (Р=Р₁+Р₂=…=Р_n) будут равны, деформации и скорости деформации будут суммироваться. (γ= γ₁+γ₂+…+ γ_n ; γ= γ·₁+ γ·₂+…+ γ·_n)

При параллельном соединении элементов – напряжения будут суммироваться (Р=Р₁+Р₂+…+Р_n), деформации и скорости деформации будут равны (γ= γ₁=γ₂=…= γ_n ; γ= γ·₁= γ·₂=…= γ·_n)

Модель упруго-вязкого тела Максвелла:

Жидкие и твердые тела – одинаковая сила сцепления.

Максвеллом было дано представление, что

механические свойства тел являются

промежуточными между идеально жидкими и

идеально твердыми телами. Последовательное

соединение элементов Гука и Ньютона.

Р=Рг=Рн γ= γг+ γн

d γ/dτ = d γг/dτ = d γн/dτ

γ = Р/Е + Рτ/η – деформация. Скорость деформации: d γ/dτ = 1/Е ·d l/dτ + Р/η

1/Е · dP/ dτ + Р/η = 0 dP/P=E/η · dτ; Интегрируем получаем: ln (P/P₀)= – E/η · τ

P=P₀ · e^-τ/λ – математическая модель Максвелла.,λ – время за которое напряжение в образце уменьшается в е раз. Характерна необратимая деформация тела.λ>>τ – релаксирует очень медленно (твердое тело), жидкое тело может вести себя как твердое.λ<<τ – тело ведет себя как жидкое, твердое тело может вести себя как жидкое.
96. Модель вязкопластического тела Бингама. Пластическая вязкость.

Комбинация всех трех моделей реологии:

(напряжение) Р<Р_Т (предела текучести) – деформация не

происходит в системе (теле) P>P_T – течение в системе

Р=Р_Т + η* · γ· – уравнение Бингама

PT (деформация)γ<0 η* - пластическая вязкость

P>P_T γ↑ (скорость деформации) γ·↑

Р = η · γ· → η = Р/ γ·= (Р_Т + η* · γ·)/ γ· = η* + Р_Т/ γ·

η – сопротивление течению всей системы; η*– течение и разрушение структуры

97. Причина неподчинения дисперсных систем закону Ньютона. Кривые течения реальных дисперсных систем. Уравнение Оствальда – Вейля.

На основе реологических свойств, тела можно разделить на жидкообразные и твердообразные.

Жидкообразные тела (Р_Т=0) можно разделить на:

Ньютоновские – системы, вязкость которых не зависит от напряжения сдвига, являющегося константой. К Ньютоновским жидкостям относятся разбавленные системы с равноосными (симметричными) частицами.

Неньютоновские – системы не подчиняющиеся закону Ньютона, вязкость зависит от напряжения сдвига; псевдопластические, дилантантные жидкости. Псевдопластические жидкости – суспензии, содержащие ассиметричные частицы, растворы полимеров. При увеличении напряжения сдвига, течение будет убыстряться. Дилантантные жидкости – дисперсные системы с большим содержанием твердой дисперсной фазы. При увеличении напряжения сдвига растет вязкость.

Неньютоновские жидкости описываются уравнением Оствальда – Вейда: Р = k · γ·

1 – Ньютоновские жидкости 1 – бингамовское тело

2- псевдопластическое твердообразное тело 2 – Псевдопластические

3 – пластическое дилантантное тело 3 – Дилантантные жидкости


98. Вязкость жидкообразных агрегативно устойчивых дисперсных систем. Уравнение Эйнштейна. Причины неподчинения коллоидных систем уравнению Эйнштейна.




η Вязкость разбавленных систем описывается уравнением

Эйнштейна: η = η₀ (1+2,5φ) – для сферических частиц;

η = η₀ (1 – 2φ) – для несферических частиц,

где η₀ – вязкость растворителя, φ – объемная доля дисперсной

фазы. Система не сжимаема. Отсутствует скольжение,

отсутствует турбулентность, отсутствует взаимодействие

между частицами η_отн = η _/ η₀ = 1+2 φ; η_уд = η_отн – 1 = 2 φ

99. Зависимость вязкости дисперсных систем от напряжения сдвига.

В концентрированной суспензии, содержание дисперсной фазы в которой больше 7% имеется придел текучести.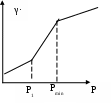

Pmin – минимальное напряжение η 1 – η_max ньютоновская вязкость

течения, полностью разрушается

структура 2 – η* пластическая вязкость

3 – η_min ньютоновская вязкость

100. Механизмы гибкости полимерной цепи: поворотно-изомерных и персистентный.

Поворотно-изомерный механизм вытекает из возможности вращения вокруг простой связи.

При вращении атомов величина валентного угла = const=>C₁-C₂

связь может находится в пространстве независимо от С_n-C_n+1.

Участок цепи который ведет себя как кинетическая отдельность и

состоит из n атомов- статистический сегмент(сегмент Куна). Так же

используется кинетический сегмент величина которого зависит от действия

внешних сил. Термодинамический сегмент- сегмент размер которого равен

р азмеру молекулы растворителя. Персистентный механизм гибкости характерен для макромолекул состоящий из 2-х переплетенных цепей (ДНК). Форма изменяется только по средствам изменения валентного угла. Гибкость располагается равномерно, макромолекула упругая червеобразная нить- персистентная цепь. Количественные характеристики гибкости: 1)при поворотно-изомерном механизме- длинна сегмента А. если длинна сегмента = длине связи, то это свободносочлененная цепь 2)С_α=ħ²/h_cc². Геометрические характеристики гибкости: 1)среднеквадратичное расстояние между концами цепи

2)радиус инерции

N- количество сегментов. При персистентном механизме гибкость

характеризуется длинной цепи(l). Cosθ(S)=c^-s/l