1. События и операции над ними. Относительные частоты и их свойства
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Свойства плотности распределения случайного вектора.
21.2 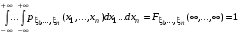 . .Теорема 1. Пусть 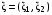 —непрерывный случайный вектор. Тогда случайные величины —непрерывный случайный вектор. Тогда случайные величины 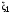 и и 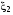 —непрерывны, причем —непрерывны, причем 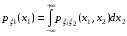 , , 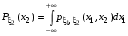 . .
Говорят, что случайный вектор 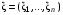 имеет равномерное распределение в области имеет равномерное распределение в области 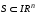 , если она непрерывна и имеет плотность. , если она непрерывна и имеет плотность.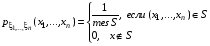 Если множество 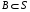 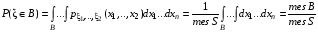 . .Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х. Теорема 2. Пусть случайная величина Х непрерывна с плотностью 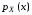 , а случайная величина , а случайная величина 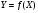 , где , где 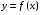 —монотонная дифференцируемая функция, тогда случайная величина Y—непрерывная и имеет плотность —монотонная дифференцируемая функция, тогда случайная величина Y—непрерывная и имеет плотность 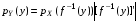 . .а) Пусть функция 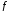 возрастает. По определению возрастает. По определению 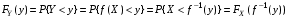 . . Продифференцируем обе части. Справа получим: 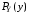 , слева— , слева— 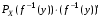 , что и требовалось , что и требовалось 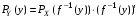 . .21.3 б) Пусть 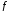 убывает. убывает. 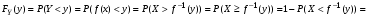 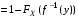 . .Продифференцировав обе части, 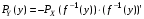 . .Покажем, как найти распределение функции случайного аргумента. Пусть аргумент Х—дискретная случайная величина А) Если различным возможным значениям аргумента функции Y, то вероятность соответствующих значений X и Y между собой равны. Б) Если различным возможным значениям Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y. Пусть задана функция 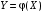 случайного аргумента Х. Требуется найти математическое ожидание этой функции, зная закон распределения аргумента. случайного аргумента Х. Требуется найти математическое ожидание этой функции, зная закон распределения аргумента.
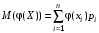 . .
Если возможны значения 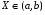 , то , то 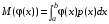 . .22. Дискретный и непрерывный случайный вектор. Свойства плотности распределения случайного вектора. Вектор ξ= ξ(ⱳ)=( 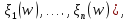 где где 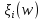 - случайные величины, называются n-мерным случайным вектором. - случайные величины, называются n-мерным случайным вектором.Таким образом, случайный вектор ξ отображает пространство элементарных исходов Ω 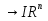 в n-мерное действительное пространство в n-мерное действительное пространство 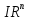 . . Случайный вектор называется дискретным, если все его компоненты-дискретные случайные величины. Случайный вектор ξ=( 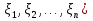 называется непрерывным, если существует неотрицательная функция p(x)= называется непрерывным, если существует неотрицательная функция p(x)=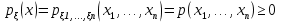 , называется плотностью распределения случайных величин , называется плотностью распределения случайных величин 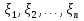 такая что функция распределения такая что функция распределения 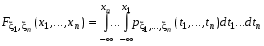 Свойства плотности распределения случайного вектора. Свойство 1. 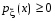 Свойство 2. 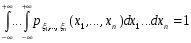 . . 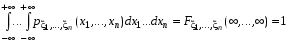 Теорема 1. Пусть ξ=(  ) – непрерывный случайный вектор. Тогда случайные величины ) – непрерывный случайный вектор. Тогда случайные величины 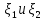 – непрерывны, причем – непрерывны, причем 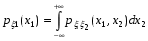 , , 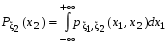 . .Свойство 3. 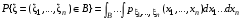 , где B , где B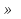 I I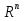 множество из пространства I множество из пространства I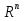 . . Говорят, что случайный вектор 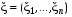 имеет равномерное распределение в области имеет равномерное распределение в области 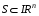 , если она непрерывна и имеет плотность. , если она непрерывна и имеет плотность. 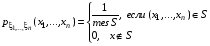 Если множество 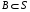 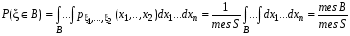 Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента Х. 22.2 Теорема 2. Пусть случайная величина Х непрерывна с плотностью 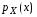 , а случайная величина , а случайная величина 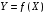 , где , где 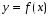 — монотонная дифференцируемая функция, тогда случайная величина Y—непрерывная и имеет плотность — монотонная дифференцируемая функция, тогда случайная величина Y—непрерывная и имеет плотность 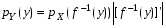 . .23. Числовые характеристики системы двух случайных величин. Ковариация, коэффициент корреляции и его свойства. Асимметрия и эксцесс. Для описания системы двух случайных величин кроме математических ожиданий и дисперсий используют и другие характеристики. К их числу относятся ковариация и коэффициент коррекции. Ковариацией между случайными величинами Х и Y называется число 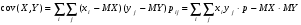 ,где ,где 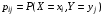 . .Для непрерывных случайных величин X и Y используют формулу 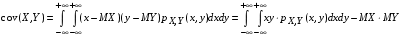 Коэффициентом корреляции между случайными величинами Х и Y называется число 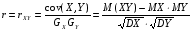 . .Свойства корреляции.
Пусть Х и Y—независимы, тогда по свойству математического ожидания 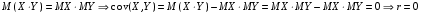 Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля. Случайные величины Х и Y называют некоррелированными если их коэффициент корреляции равен 0. Замечание. Коэффициент корреляции характеризует тенденцию случ. величин Х и У и лин. зависимости. Чем больше по абсол. величине коэффициент корреляции, тем выше тенденция к лин. зависимости. Коэффициентом асимметрии случайной величины Х называется число 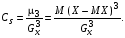 Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию. Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.Эксцессом случайной величины Х называется число 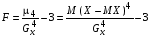 . Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения. . Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.24. Задачи математической статистики. Генеральная совокупность, выборка. Задачи мат.статистики: Оценка неизвестных параметров     Генеральная и выборочная совокупности.  Свойства генеральной совокупности изучают на основании анализа статистических данных, под которыми понимают значения случайно величины, которые получены в результате повторения эксперимента(наблюдение над случайной величиной). Свойства генеральной совокупности изучают на основании анализа статистических данных, под которыми понимают значения случайно величины, которые получены в результате повторения эксперимента(наблюдение над случайной величиной). 24.2 Совокупность независимых случ.величин 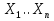 каждая из которых имеетто же распределение, что и случайная величина X называется случайной выборкой из генеральной совокупности X и обозначаетс каждая из которых имеетто же распределение, что и случайная величина X называется случайной выборкой из генеральной совокупности X и обозначаетс     Выборка наз. повторной если объект возвращается в генеральную совокупность. Бесповторной – объект не возвращается. Типический отбор – отбор при котором неоднородная генеральная совокупность разбивается на однородные группы, из которых потом и произв. отбор. Механический отбор производится через определенный интервал.   25. Эмпирическая функция распределения. Генеральные и выборочные начальные и центральные моменты. Введем для реализации 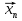 случайной выборки случайной выборки 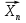 эмпирическую функцию распределения: F* эмпирическую функцию распределения: F*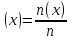 , где n – объем выборки. Эмпирическая функция распределения кусочно постоянна и изменяется скачками в каждой точке , где n – объем выборки. Эмпирическая функция распределения кусочно постоянна и изменяется скачками в каждой точке 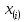 ( (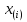 – i-ая варианта). Эмпирическая функция распределения обладает всеми свойствами функции распределения, рассмотренными в курсе лекций по теории вероятностей. Свойства функции распределения: – i-ая варианта). Эмпирическая функция распределения обладает всеми свойствами функции распределения, рассмотренными в курсе лекций по теории вероятностей. Свойства функции распределения: 1. Значения функции распределения принадлежат отрезку [0;1]. 2. Функция распределенияF* 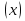 – неубывающая функция. – неубывающая функция.3. Если x(1) – наименьшее значение выборки, а x(k) – наибольшее, то F* 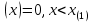 , ,F* 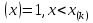 . Таким образом, эмпирическая функция распределения, построенная с помощью выборки из генеральной совокупности, является . Таким образом, эмпирическая функция распределения, построенная с помощью выборки из генеральной совокупности, являетсяприближением теоретической функции распределения, ее статистическиманалогом. Всем числовым характеристикам генеральной совокупности (теоретическим или генеральным) можно поставить в соответствие их выборочные аналоги (статистические аналоги), определенные на выборке. Теоретические начальный (��k) и центральный (m k) моменты k-того порядка определяются следующим образом: 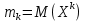 , (1) , (1)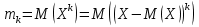 (2) (2)Здесь ��(��) – математическое ожидание, которое можно найти, зная плотность распределения непрерывной случайной величины или закон распределения дискретной случайной величины по формулам (3) и (4) соответственно. 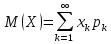 , (3) , (3)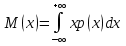 (4) (4)Определим выборочные начальный 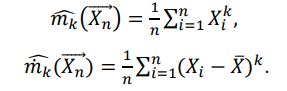 Здесь 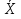 – выборочное среднее: – выборочное среднее: 2-го порядка: 26.Статистическое распределение выборки. Полигон и гистограмма Пусть из генеральной совокупности извлечена выборка, причём x1 наблюдалось n1 раз, x2-n2 раз, и т.д.xk - nk раз и 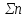 i = n - объём выборки. i = n - объём выборки.Наблюдаемые значения xi называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа наблюдений называют частотами, а их отношения к объёму выборки 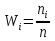 - относительными частотами. - относительными частотами.Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот. Следует отметить, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами. Пусть nx - число наблюдений, при которых наблюдалось значение признака, меньшее- объём выборки. Относительная частота события X 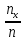 есть функция от x. Так как эта функция находится опытным путём, то её называют эмпирической. есть функция от x. Так как эта функция находится опытным путём, то её называют эмпирической.Эмпирической функцией распределения называется функция F(x), определяющая для каждого значенияотносительную частоту события X 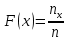 . .В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события X Функция F(x) обладает следующими свойствами: значения функции принадлежат отрезку [0;1]; F(x)- неубывающая функция; если x1- наименьшая варианта, то F(x)=0 при 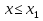 ; если xk - наибольшая варианта, то F(x)=1при ; если xk - наибольшая варианта, то F(x)=1при 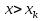 . .Полигоном частот называют ломаную линию, отрезки которой соединяют  Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1;W1), (x2;W2), . . . , (xk;Wk). |

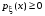
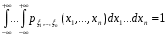 .
.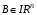 —множество из пространства IRn.
—множество из пространства IRn.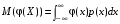 .
.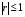 .
.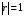 необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е.
необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е.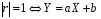 с вероятностью 1.
с вероятностью 1.