1. События и операции над ними. Относительные частоты и их свойства

• Название: 1. События и операции над ними. Относительные частоты и их свойства
• Дата: 25.06.2019
• Размер: 0.83 Mb.
• Имя файла: TVIMS.docx
• Тип: Документы; #82957
• страница: 3 из 6

2) Постоянный множитель можно выносить за знак математического ожидания:

M(CX)=CM(X).

Если случайная величин Х имеет ряд распределения

X	x1	x2	…	xn	…
P	p1	p2	…	pn	…

Ряд распределения случайной величины СХ

СХ	Сx1	Сx2	…	Сxn	…
Р	p1	p2	…	pn	…

Математическое ожидание случайной величины СХ

.
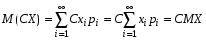15.2

Случайные величины X₁,X₂,…,X_n называются независимыми, если для любых числовых множеств B₁,B₂,…,B_n .

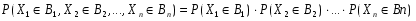Если взять B₁=]-∞, x₁[; B₂=]-∞, x₂[; …; B_n=]-∞,x_n[, то .

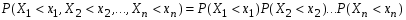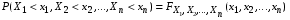—совместимая функция распределения случайных величин Х₁,Х₂,…,Х_n. Таким образом, 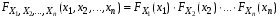. Данное равенство также можно взять в качестве определения независимости случайных величин.

3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

.

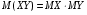Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

4) Математическое ожидание суммы двух случайных величин рано сумме математических ожиданий слагаемых:.

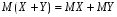Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.

Теорема 1. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: .

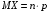Будем рассматривать в качестве случайной величины Х число появлений события А в n независимых испытаниях. Очевидно, общее число Х появлений события А в этих испытаниях складывается из чисел появлений события в отдельных испытаниях. Поэтому если Х₁—число появлений события в первом испытании, Х₂—во втором,…, Х_n—в n-ом, то общее число появлений события 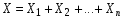. По свойству 4:

.

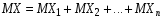Согласно примеру 2 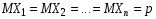. Таким образом, получим .

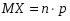16. Дисперсия дискретной случайной величины и её свойства.

Дисперсией случайной величины называется число 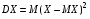. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания.

Свойства дисперсии.

1. 
   Дисперсия постоянной величины С равна 0. DC=0.
   

.

2. 
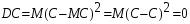   Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
   

.

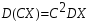Доказательство:

3. 
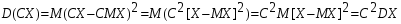
   Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: .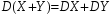
   

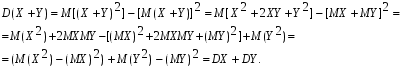Доказательство:

Следствие. Дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин.

17. Теоремы о математическом ожидании и дисперсии числа появлений события в независимых испытаниях. Начальные и центральные моменты.

Теорема 1. Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события Х в каждом испытании: .

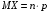если Х1—число появлений события в первом испытании, Х2—во втором,…, Хn—в n-ом, то общее число появлений события .

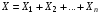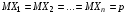. Таким образом, получим .

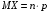Дисперсией случайной величины называется число 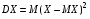. Дисперсия является мерой разброса значений случайной величины вокруг ее математического ожидания. Средним квадратическим отклонением случайной величины Х называется число .

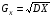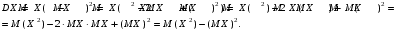Теорема 2. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятность появления и непоявления события в одном испытании: .
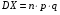Случ. велич. Х—число появлений события А в n независимых испытаниях 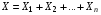, где Хi—число наступлений событий в i-ом испытании, взаимно независимые, т.к. исход каждого испытания не зависит от исходов остальных.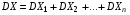;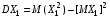.Т.к. MX₁=p.

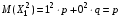, то 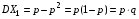. Очевидно, что дисперсия остальных случайных величин также равна pq, откуда .

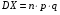Начальным моментом порядка к случайным величинам Х называют мат.ожид. случ. величины Х^k: 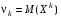. В частности, , .

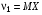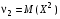Пользуясь этими моментами, формулу для вычисления дисперсии 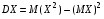можно записать так: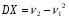.Кроме моментов случ. величины Х целесообразно рассматривать моменты отклонения Х-ХМ.

Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х-МХ)^k.

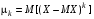. В частности ,

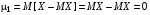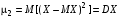. Следовательно, 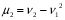. Исходя из определения центрального момента и пользуясь свойствами мат. ожид., можно получить формулы: ; .

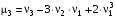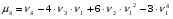Моменты более высоких порядков применяются редко.

Замечание. Моменты, определенные выше, называют теоретическими. В отличие от теоретических моментов, моменты, которые вычисляются по данным наблюдений, называют эмпирическими.


18. Непрерывные случайные величины. Свойства плотности распределения.

О. Говорят, что случайная величина Х имеет плотность вероятности или плотность распределения вероятностей 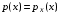, если существует функция p(x) такая, что функция распределения 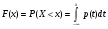(1).

О. Случайная величина называется непрерывной, если она имеет плотность распределения.

Пусть р(х)—непрерывная функция. Тогда 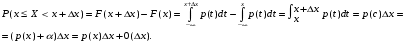Где 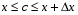, α—бесконечно малая величина при Δх→0.

Т.к. 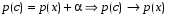, при Δх→0. Таким образом, .

.

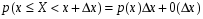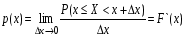Свойства плотности распределения.

1. 
   .
   
2. 
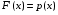   Плотность распределения—неотрицательная функция: .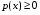
   

Поскольку F(x)—неубывающая функция, то F’(x)≥0. Следовательно 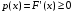—неотрицательная функция.

Геометрически это свойство означает, что график плотности распределения расположен либо над осью ох, либо на этой оси. График плотности распределения называют кривой распределения.

3. 
   Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице:
   

.

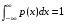В формуле (1) подставим х=+∞, 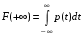. Поскольку 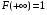, то .

4. 
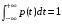   Вероятность того, что непрерывная случайная величина Х примет значение из множества В, равна интегралу по множеству В от плотности распределения.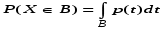
   

19. Равномерное, показательное и нормальное распределения и их числовые характеристики.

Говорят, что случайная величина Х равномерно распределена на отрезке [a, b], если она непрерывна и имеет плотность вероятности: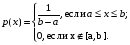Найдем функцию распределения равномерно распределенной случайной величины X.

а) x;

б) a≤x≤b.

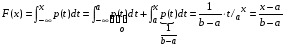в) x>b.



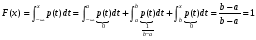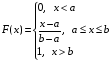
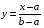, если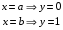

Говорят, что случайная величина Х имеет показательное (экопоненциальное) распределение с параметром λ>0, если она непрерывна и имеет плотность распределения

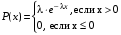; обозначают ХM(λ).

Найдем функцию распределения показательно распределенной случайной величины Х.

а) x≤0

.

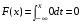б) x>0

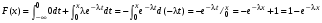
19.2

Таким образом

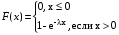
Говорят, что случайная величина Х имеет нормальное распределение с параметрами a, G2, если она непрерывна и имеет плотность 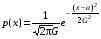. Обозначение ХN(a, G2), те Х имеет нормальное распределение с параметрами a, G2.

График плотности нормально распределенной случайной величины имеет вид:




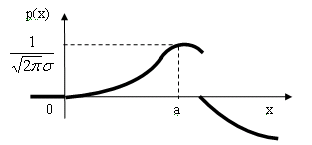
Если случайная величина ХN(0,1), то говорят, что случайная величина Х имеет стандартное нормальное распределение. В этом случае плотность обозначается 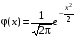. Через N(x) обозначим 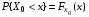, где Х0N(0,1).

.

.




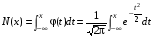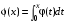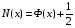
20. Теорема о нормальном распределении. Критерии независимости дискретной и непрерывной случайных величин.

• 
  Случайная величина Х имеет нормальное распределение с параметрами a, G², если она непрерывна и имеет плотность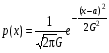 . Обозначение ХN(a, G²), те Х имеет нормальное распределение с параметрами a, G².
  

График плотности нормально распределенной случайной величины имеет вид:

• 
  Любая функция (правило, характеристика), позволяющая вычислить вероятность того, что случайная величина Х принадлежит В—числовому множеству на прямой, т.е. P(XB), называется законом распределения случайной величины Х.
  
  1. 
     F(x)—функция распределения является законом распределения любой случайной величины. .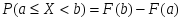
     
  2. 
     Ряд распределения дискретной случайной величины также является законом распределения дискретной случайной величины.
     
  3. 
     Плотность распределения непрерывной случайной величины p(x) является законом распределения непрерывной случайной величины.
     

.

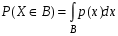Теорема (Критерий независимости дискретных случайных величин).

Для того чтобы дискретные случайные величины Х₁,…,Х_n были независимы, необходимо и достаточно, чтобы для любых действительных чисел х₁,…,х_n выполнялось соотношение .

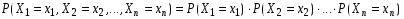Теорема (Критерий независимости для непрерывных случайных величин).

Для того чтобы непрерывные случайные величины Х₁, Х₂,…,Х_n были независимыми, необходимо и достаточно, чтобы для любых действительных чисел х₁,…,х_n выполнялось соотношение

.

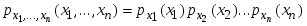20.2

Здесь 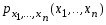—совместимая плотность распределения случайных величин Х₁,…,Х_n, то есть совместимая функция распределения случайных величин Х₁,…,Х_n

.

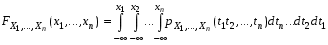Пример: Предположим, что случайная величина 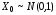. Вероятность, что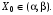

.

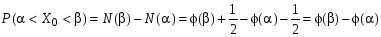Пусть .



.

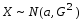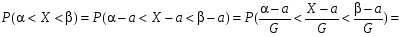
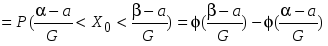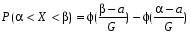, где 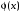—функция Лапласа.

Замечание. Необходимо отметить, что φ(t)—четная функция, т.е. φ(-х)=φ(х); функция Лапласа 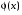— нечетная, т.е.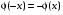; функция стандартного нормального распределения N(x) обладает свойством N(x)+N(-x)=1.


21. Случайный вектор. Свойства функции распределения случайного вектора.

Вектор 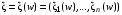, где 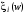—случайные величины, называются n-мерным случайным вектором.

Таким образом, случайный вектор 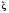отображает пространство элементарных исходов Ω→IRⁿ в n-мерное действительное пространство IRⁿ.

Функция

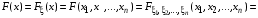
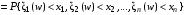называется функцией распределения случайного вектора 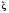или совместной функцией распределения случайных величин .

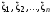Свойства функции распределения случайного вектора.

1. 
   .
   
2. 
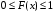   Функция распределения случайного вектора неубывающая по каждому аргументу.
   

Пусть x₁1, тогда событие .

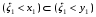Тогда 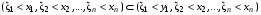. По свойству вероятности если 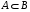, то 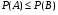, получим 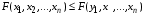. Т.е. функция не убывает по первому аргументу. Аналогично для любого аргумента.

3. 
   .
   

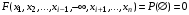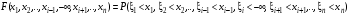=0

4. 
   
   

.







=.

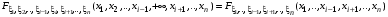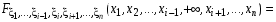
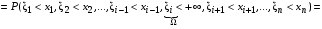
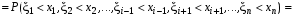
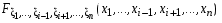Случайный вектор называется дискретным, если все его компоненты—дискретные случайные величины.

Случайный вектор 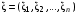называется непрерывным, если существует неотрицательная функция p(x) = p_(x) =p_{1,….n}(x_1,…,x_n)=p(x₁,…,x_n)≥0, называется плотностью распределения случайных величин 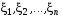такая, что функция распределения .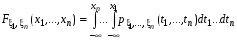