1. События и операции над ними. Относительные частоты и их свойства
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
ПРОДОЛЖЕНИЕ 29 Оценка для математического ожидания при неизвестной дисперсии Определим оценку для математического ожидания при неизвестной дисперсии. Рассмотрим статистику T( 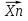 ; μ )= ; μ )=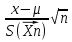 Здесь используется статистика 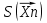 квадрат которой является несмещенной и состоятельной оценкой дисперсии квадрат которой является несмещенной и состоятельной оценкой дисперсии 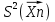 = = 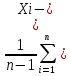 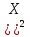 Статистика T( 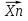 ; μ ) является центральной статистикой, имеет распределение Стьюдента с n-1 степенями свободы и ее функция рас-пределения не зависит от параметров μ и ; μ ) является центральной статистикой, имеет распределение Стьюдента с n-1 степенями свободы и ее функция рас-пределения не зависит от параметров μ и 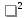 . .Плотность вероятности распределения Стьюдента определяется параметром n – объемом выборки, или числом степеней свободы k = n – 1. S(t,n) = Bn(1+ 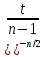 Bn = 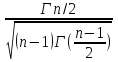 . . Соответствующая система уравнений имеет вид 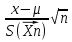 = t1−�� (n-1), = t1−�� (n-1),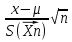 = t �� (n-1), = t �� (n-1),где ����(��−1) – квантиль уровня q распределения Стьюдента с n – 1 степенями свободы. Учитывая, что ��1−�� (��−1) = − ����(��−1) получаем нижнюю и верхнюю границы доверительного интервала для парамет-ра μ при γ=1– α – β. μ =��̅− 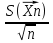 t1−�� (n-1), t1−�� (n-1), μ =��̅+ 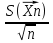 t1−�� (n-1). t1−�� (n-1). Доверительный интервал для мат. ожидания с неизвестной дисперсией (��̅− 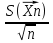 t1−�� (n-1), ��̅+ t1−�� (n-1), ��̅+ 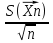 t1−�� (n-1)) t1−�� (n-1))Смысл полученного соотношения: с надежностью γ можно утверждать, что доверительный интервал (��̅− 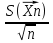 t1−�� (n-1), ��̅+ t1−�� (n-1), ��̅+ 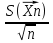 t1−�� (n-1)) покрывает неизвестный параметр ��. t1−�� (n-1)) покрывает неизвестный параметр ��. 30. Функция двух случайных аргументов. Формула свёртки. Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y: 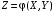 . .Далее на примерах будет показано, как найти распределение функции 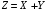 по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если Х—погрешность показаний измерительного прибора (распределена равномерно), то возникает задача—найти закон распределения суммы погрешностей по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если Х—погрешность показаний измерительного прибора (распределена равномерно), то возникает задача—найти закон распределения суммы погрешностей 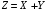 Случай 1. Общий случай. Пусть Х и Y—независимые случайные величины, принимающие значения 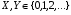 . Обозначим через . Обозначим через 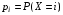  , , 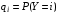 , , 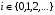 . .Z=X+Н. Обозначим через 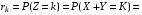 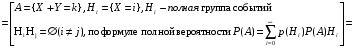 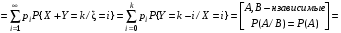 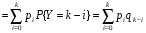 . .Таким образом, 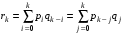 —формула свертки. —формула свертки.Случай 2. Пусть Х и Y—непрерывные случайные величины. Теорема. Если Х и Y—независимые непрерывные случайные величины, то случайная величина Z=X+Y—также непрерывна, причем плотность распределения случайной величины Z 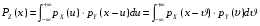 — формула свертки. — формула свертки. |
