1. События и операции над ними. Относительные частоты и их свойства
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
ПРОДОЛЖЕНИЕ 26 При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длиной h и находят ni- сумму частот вариант, попавших в i-ый интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению 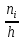 (плотностью частоты). Площадь частичного -го прямоугольника равна (плотностью частоты). Площадь частичного -го прямоугольника равна 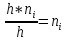 - сумме частот вариант, попавших в i-ый интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки n. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению - сумме частот вариант, попавших в i-ый интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки n. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению 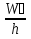 (плотность относительной частоты). (плотность относительной частоты).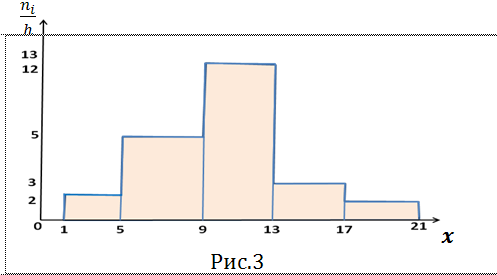 На рис. 3 изображена гистограмма частот по данному распределению выборки объёма n=100.
27. Точечные оценки неизвестных параметров. Несмещённые, состоятельные и эффективные оценки. Задача оценки параметров возникает при рассмотрении параметрической модели. В этом случае полагают, что закон распределения генеральной совокупности имеет вид: F(x; 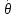 ). ).То есть функция распределения генеральной совокупности известна с точностью до параметра 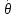 = (θ1, … , θn), значение которого и нужно оценить по данным измерения. = (θ1, … , θn), значение которого и нужно оценить по данным измерения.В математической статистике рассматривают два вида оценок: точечные и интервальные. Статистику 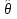 ( (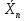 ), выборочное значение ), выборочное значение 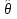 = = 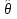 ( (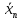 ) которой для любой реализации ( ) которой для любой реализации (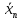 ) принимают за приближенное значение параметра ) принимают за приближенное значение параметра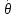 , называют точечной оценкой, а выборочное значение , называют точечной оценкой, а выборочное значение 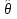 = =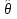 ( (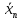 )– значением точечной оценки. )– значением точечной оценки.Задача оценки параметров сводится к нахождению неизвестного параметра распределения по результатам измерений (реализации случайной выборки). В качестве оценки выбирают некоторую функцию от измеренных величин. Для того, чтобы определить «оптимальную» для оцениваемого параметра статистику, необходимо, чтобы она удовлетворяла ряду условий. Так, например, оценка должна быть состоятельной. Предпочтительнее использовать эффективные оценки и т. д. Состоятельная оценка Статистику 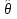 = = 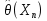 называют состоятельной оценкой параметра θ, если с ростом объема выборки n она сходится по вероятности к оцениваему параметру θ. называют состоятельной оценкой параметра θ, если с ростом объема выборки n она сходится по вероятности к оцениваему параметру θ. 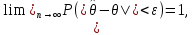 где ε > 0. То есть почти достоверным является событие, заключающееся в том, что состоятельная оценка отклоняется по модулю от значения параметра на сколь угодно малую положительную величину, если объем выборки достаточно велик. где ε > 0. То есть почти достоверным является событие, заключающееся в том, что состоятельная оценка отклоняется по модулю от значения параметра на сколь угодно малую положительную величину, если объем выборки достаточно велик.Несмещенная оценка Статистику 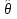 = = 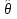 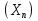 , называют несмещенной оценкой параметра θ, если ее математическое ожидание совпадает с θ для любого фиксированного n. , называют несмещенной оценкой параметра θ, если ее математическое ожидание совпадает с θ для любого фиксированного n.�� 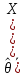 ) = ��. ) = ��.Оценка является смещенной с параметром смещения b, если это равенство не выполняется. ����(��) = �� 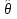 ( (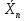 )− ��. )− ��.Смещение оценки можно устранить, введя соответствующую поправку. Иногда достаточно найти асимптотически несмещенную оценку. Оценка 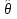 = = 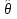 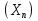 является асимптотически несмещенной, если при n→∞ она сходится по вероятности к своему математическому ожиданию для любого ε > 0. является асимптотически несмещенной, если при n→∞ она сходится по вероятности к своему математическому ожиданию для любого ε > 0.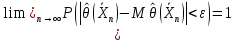 27.2 Эффективная оценка Пусть имеются две несмещенные оценки 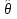 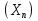 и и 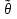 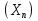 , такие, что для дисперсий этих оценок , такие, что для дисперсий этих оценок 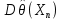 и �� и ��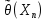 выполняется неравенство: выполняется неравенство: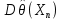 ≤ �� ≤ ��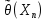 . (3.3) . (3.3)Очевидно, что при выборе статистики, используемой для получения оценки параметра, следует предпочесть 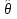 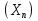 – статистику с меньшей дисперсией. – статистику с меньшей дисперсией.Если в некотором классе несмещенных оценок параметра имеется такая 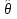 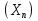 , что неравенство (3.3) выполняется для всех , что неравенство (3.3) выполняется для всех 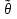 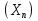 , то говорят, что , то говорят, что 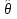 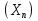 является эффективной в данном классе оценок. является эффективной в данном классе оценок.Таким образом, дисперсия эффективной оценки параметра в некотором классе является минимальной среди дисперсий всех оценок. Эффективную оценку называют также несмещенной оценкой с минимальной дисперсией, или оптимальной оценкой. 28. Методы моментов и максимального правдоподобия. Метод максимального правдоподобия, сокращенно ММП - это общий метод оценивания параметров генеральной совокупности с помощью максимизации функции правдоподобия L выборки. Функция правдоподобия L есть совместное распределение выборки, которое представляет собой функцию параметра Если выборка имеет непрерывное распределение, функция правдоподобия L описывается совместной плотностью распределения В случае, если элементы выборки Величину функция правдоподобия можно считать мерой правдоподобия значения θ при заданной реализации x. Пусть L - функция правдоподобия выборки; при наблюдаемых значениях - является функцией параметров θ. Тогда оценками максимального правдоподобия θ называются наиболее правдоподобные значения максимизирующие функцию L. = Очевидно, оценки зависят от наблюдений Часто проще искать точку максимума функции Пусть θ - это элемент пространства 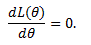 Метод моментов состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка. Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (12) относительно неизвестного параметра, тем самым получим его точечную оценку. ПРОДОЛЖЕНИЕ 28 Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка: Учитывая, что 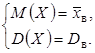 Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему относительно неизвестных параметров, тем самым получим их точечные оценки. Разумеется, для вычисления выборочной средней и выборочной дисперсии надо располагать выборкой 29.Интервальные оценки неизвестных параметров. Доверительные интервалы для математического ожидания и дисперсии. Пусть имеется выборка х1,х2,…,хn объема n из ген. совокупности ф-ция распред. которой F(x|a) зависит от неизвест. па-ра a , при построении точечной оценки па-ра а невозможно оценить погрешность приближения его оценкой а^=a^(x1,x2,…,xn), поэтому часто выгоднее пользоваться интервальной оценкой па-ров, основанной на построении некоторого интервала внутри которого с опред. вероятностью находится неизвест. па-р а Если аn^ - точечная оценка параметра а, то чем меньше |a-an^|, тем выше качество оценки, т.е. число  >0 | |a-an^|< >0 | |a-an^|< характеризует точность оценки. характеризует точность оценки.Опред. Случ. величина аh=ah(x1,…,xn) и ab=ab(x1,…,xn), являющиеся функциями от выборочных значений наз. соответственно нижним и верхним двусторонним доверительным пределом для неизвестного параметра a c надежностью (коэф. доверия, доверительной вероятностью) P(0,5 Замечание. Надежность P выбирается близкой к единице (0,9;0,95 и т.д.), а уровень значимости близки к нулю (0,1; 0,05). Если а^ - точечная оценка параметра a и а^-   - наз. точностью интервальной оценки. - наз. точностью интервальной оценки.Рассмотрим случайную выборку объема n 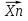 из генер. совокупности X, распределенную по норм. закону с параметра-ми μ и из генер. совокупности X, распределенную по норм. закону с параметра-ми μ и 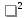 . . Определим оценку для мат. ожидания при известной дисперсии. T( 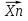 ; μ )= ; μ )=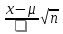 Можно показать, что эта статистика имеет стандартное норм. распределение с параметрами μ = 0 и 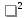 . = 1, т.е. является центральной статистикой. T( . = 1, т.е. является центральной статистикой. T(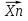 ; μ) является функция убывающая по μ. ; μ) является функция убывающая по μ. Соответсвующая система уравнений имеет вид: 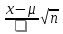 =U1−��, =U1−��, 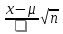 =U��, =U��,где uq – квантиль стандартного норм. распределения. Учитывая, что U1-α = –Uα, получаем нижнюю и верхнюю границы доверительного интервала для параметра μ при γ=1–α – β. μ =��̅− 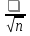 U1−��, U1−��, μ = ��̅+ 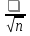 U1−��. U1−��. Доверительный интервал для мат. ожидания с известной дисперсией записывается следующим образом: (��̅− 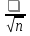 U1−��, μ = ��̅+ U1−��, μ = ��̅+ 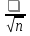 U1−��). U1−��). Смысл полученного соотношения: с надежностью γ можно утверждать, что доверительный интервал (��̅− 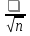 U1−��, μ = ��̅+ U1−��, μ = ��̅+ 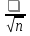 U1−��) покрывает неизвестный параметр ��. U1−��) покрывает неизвестный параметр ��. |
