Док-во: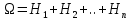 ; ;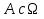 ; ;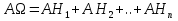 ; ;
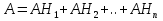 ; ; 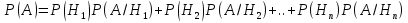 ,чтд ,чтд
Замечание: При применении формулы полной вероятности, события 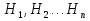 называют гипотезами. называют гипотезами.
Теорема (Формула Байеса) – Пусть события 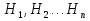 образуют полную группу. A – некоторое событие, которое может произойти совместно с любым из событий, образующих полную группу, причем то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, причем образуют полную группу. A – некоторое событие, которое может произойти совместно с любым из событий, образующих полную группу, причем то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, причем 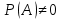 , тогда условные вероятности событий полной группы при условии наступления события A находятся по формуле Байеса: , тогда условные вероятности событий полной группы при условии наступления события A находятся по формуле Байеса:
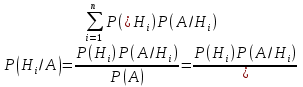
Замечание: В формуле Байеса вероятности 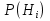 называются априорными вероятностями гипотез, а называются априорными вероятностями гипотез, а 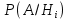 называются апостериорными вероятностями гипотез. называются апостериорными вероятностями гипотез.
Пример (Формула полной вероятности): Имеются две урны. В первой – 3б и 5ч шара, во второй – 4б и 3ч. Из первой наудачу взят шар и переложен во вторую. После, из второй урны извлечен наудачу шар. Какова вероятность того, что он белый.
A – из второй урны извлечен белый шар; 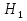 – из первой урны во вторую был переложен белый шар; – из первой урны во вторую был переложен белый шар; 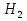 – из первой урны во вторую был переложен черный – из первой урны во вторую был переложен черный
Решение: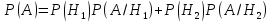 ; ;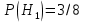 ; ;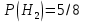 ; ;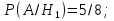 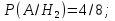
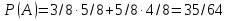
Ответ: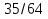
9. Испытания Бернулли. Формула Бернулли.
Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называем успехом и неудачей. 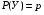 , , 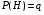 , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию.
Элементарным исходом будет являться: (w1,w2,…,wn), 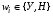 . .
Всего таких исходов 2n.
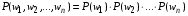 . (1) . (1)
Формула (1) показывает, что события независимы.
Обозначим через µ число успехов в n испытаниях Бернулли. 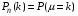 — вероятность того, что в n испытаниях произошло k успехов. — вероятность того, что в n испытаниях произошло k успехов.
Раcсм. соб. 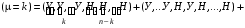 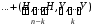 . По теореме сложения получим . По теореме сложения получим
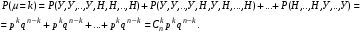 Таким образом, получим Таким образом, получим
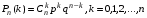 —формула Бернулли. —формула Бернулли.
10. Полиномиальное распределение.
Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek, P(Ei)=pi,  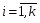 . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле: . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле:
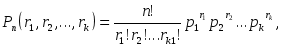 где где 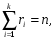 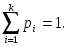
Эта формула полиномиальное распределения, обобщающая формулу Бернулли.
11. Теорема Пуассона
Теорема(Пуассона): Пусть производятся n-независимых испытаний в каждом из которых событие А наступает с вероятностью p, тогда если число испытаний неограниченно возрастает, а вероятность стремится к 0 причем n=p=const , то вероятность того, что событие А появится к раз , в n независимых испытаниях находится по формуле:
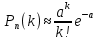 – формула Пуассона – формула Пуассона
Доказательство: По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях
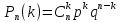 , где q=1-p. , где q=1-p.
Отсюда
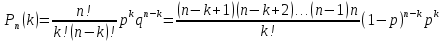
По условию a=np => 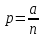
Подставляя, получим
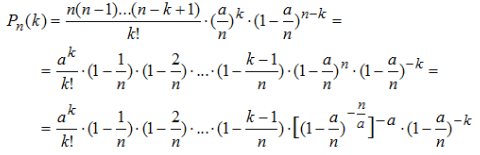
Перейдем к пределу при n->∞, т.е.
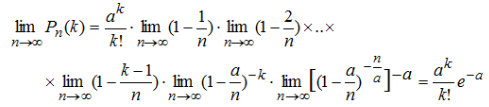
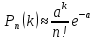 – формула Пуассона – формула Пуассона
Теоремой удобно использовать, когда p->0, a=np≤10. Существует специальные таблицы, в которых приведены значения вероятностей для различных а и k.
Формулой Бернулли удобно пользоваться, когда значение n не очень велико. Если же n достаточно велико, то удобнее пользоваться приближенными формулами, одна из которых содержится в следующей теореме.
12. Локальная и интегральная теоремы Муавра Лапласа.
Локальная теорема Лапласа
Если вероятность p появления случайного события в каждом испытании постоянна, то вероятность того, что в n испытаниях событие A наступит ровно m раз, приближённо равна:
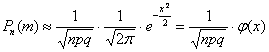 , где , где
При этом, чем больше n, тем рассчитанная вероятность будет лучше приближать точное значению , полученное по формуле Бернулли. Рекомендуемое минимальное количество испытаний – примерно 50-100, в противном случае результат может оказаться далёким от истины. Кроме того, локальная теорема Лапласа работает тем лучше, чем вероятность p ближе к 0,5, и наоборот – даёт существенную погрешность при значениях p, близких к нулю либо единице. По этой причине ещё одним критерием эффективного использования формулы является выполнение неравенства
Интегральная теорема Лапласа
Если вероятность p появления случайного события A в каждом испытании постоянна, то вероятность того, что в n испытаниях событие A наступит не менее и не более раз (от до раз включительно), приближённо равна:
где 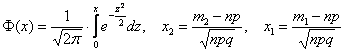 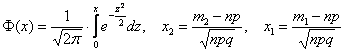
При этом количество испытаний, разумеется, тоже должно быть достаточно большим и вероятность p не слишком мала/велика (ориентировочно ), иначе приближение будет неважным либо плохим.
Начиная с x=4, можно считать, что Ф(x)=0,5, или, если записать строже:
Кроме того, функция Лапласа нечётна: Ф(-х)=-Ф(х), и данное свойство активно эксплуатируется в задачах.
13. Случайные величины. Функция распределения и её свойства.
Случайной величиной Х наз. ф-ция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R.
Пример. Пусть дважды подбрасывается монета. Тогда 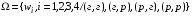 .Рассмотрим случ. величину Х–число выпадений герба на пространстве элементарных исходов Ω. Множество возможных значений случайной величины:2,1,0. .Рассмотрим случ. величину Х–число выпадений герба на пространстве элементарных исходов Ω. Множество возможных значений случайной величины:2,1,0.
w
|
(г,г)
|
(г,р)
|
(р,г)
|
(р,р)
|
X(w)
|
2
|
1
|
1
|
0
|
Множество значений случ. величины обознач. Ωх. Одной из важных характер. случ. величины является функция распределения случайной величины.
Функцией распределения случайной величины Х наз. функция F(x) действительной переменной х, определяющая вероятность того, что случ. величина Х примет значение, меньшее некоторого фиксированного числа х.
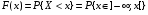 . .
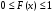 . .
Если рассматривать Х как случ. точку на оси ох, то F(x) с геометрической точки зрения—это вероятность того, что случайная точка Х в результате реализации эксперимента попадет левее точки х.
Свойства функции распределения.
1)Функция распределения F(x)–неубывающая функция, т.е. для 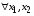 таких что x12 таких что x12 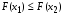 .Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е. .Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е. 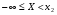 , представим в виде объединения двух несовместимых событий , представим в виде объединения двух несовместимых событий
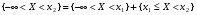 . .
Тогда по теореме сложения вероятностей получим 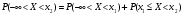 , т.е. , т.е.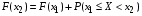 . Поскольку . Поскольку 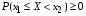 , то , то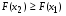 . .
2)Для любых 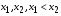 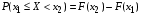
Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤.
3)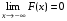 , , 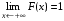 . .
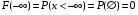 , , 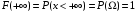 . .
4)Функция F(x) непрерывна слева. (т.е. 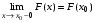 ). ).
5)Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.
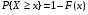 . .
Достоверное событие {-∞. Найдем их вероятно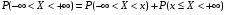 .Поскольку вероятность достоверного события равна единице, то .Поскольку вероятность достоверного события равна единице, то 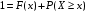 . Отсюда . Отсюда 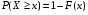 . .
14. Дискретные случайные величины. Закон распределения. Биномиальное, геометрическое и распределение Пуассона.
Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т.е. Ωх—конечно или счетно. Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (хi, рi), где xi—возможные значения случайной величины, а pi—вероятности, с которыми случайная величина принимает эти значения, т.е. 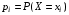 , причем , причем 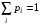 . Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности. . Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
-
X
|
x1
|
x2
|
…
|
xn
|
…
|
P
|
p1
|
p2
|
…
|
pn
|
…
|
Такая таблица называется рядом распределения дискретной случайной величины.
Говорят, что дискретная случайная величина Х имеет биномиальное распределение с параметрами (n,p), если она может принимать целые неотрицательные значения 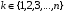 с вероятностями с вероятностями 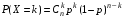
-
Пример. µ—число успехов в n испытаниях. µ имеет биномиальное распределение с параметрами (n,p). Обозначают XB (n,p), т.е. случайная величина Х имеет биномиальное распределение с параметрами (n,p).
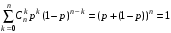
Говорят, что случайная величина Х имеет распределение Пуассона с параметром λ (λ>0), если она принимает целые неотрицательные значения 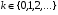 с вероятностями с вероятностями 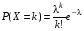 . .
-
Говорят, что случайная величина Х имеет геометрическое распределение с параметром р (0<р<1), если она принимает натуральные значения 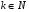 с вероятностями с вероятностями 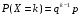 , где q=1-p. , где q=1-p.
X
|
1
|
2
|
3
|
…
|
k
|
…
|
P
|
p
|
qp
|
q2p
|
…
|
qk-1p
|
…
|
15. Математическое ожидание дискретной случайной величины и его свойства.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х через MX или М(Х). Если случайная величина Х принимает конечное число значений, то 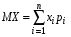 . .
Если случайная величина Х принимает счетное число значений, то 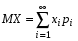 , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание дискретной случайной величины—это неслучайная величина (т.е. число, постоянная).
Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Свойства математического ожидания:
1) Математическое ожидание постоянной величины равно самой постоянной:
M(C)=C.
Будем рассматривать постоянную С как дискретную случайную величину, которая принимает одно возможное значение С с вероятностью 1. Следовательно, 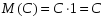 . Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х. . Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х.
|
 Скачать 0.83 Mb.
Скачать 0.83 Mb.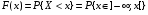 .
.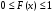 .
.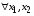 таких что x1
таких что x1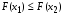 .Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е.
.Пусть х1 и х2 принадлежат множеству Ωх и х1<х2.Событие, состоящее в том, что Х примет значение, меньшее, чем х2, т.е. 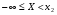 , представим в виде объединения двух несовместимых событий
, представим в виде объединения двух несовместимых событий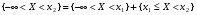 .
.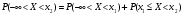 , т.е.
, т.е.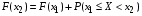 . Поскольку
. Поскольку 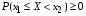 , то
, то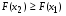 .
.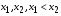
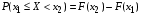
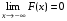 ,
, 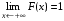 .
.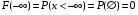 ,
, 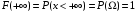 .
.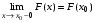 ).
).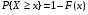 .
.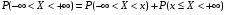 .Поскольку вероятность достоверного события равна единице, то
.Поскольку вероятность достоверного события равна единице, то 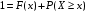 . Отсюда
. Отсюда 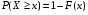 .
.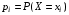 , причем
, причем 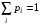 . Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.
. Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности.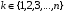 с вероятностями
с вероятностями 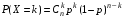
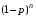
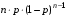
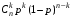
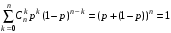
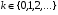 с вероятностями
с вероятностями 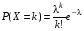 .
.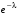
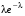
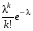
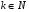 с вероятностями
с вероятностями 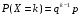 , где q=1-p.
, где q=1-p.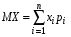 .
.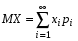 , причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
, причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. 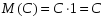 . Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х.
. Замечание. Произведение постоянной величины С на дискретную случайную величину Х определяется как дискретная случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х, вероятности возможных значений СХ равны вероятностям соответствующих возможных значении Х.
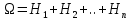 ;
;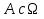 ;
;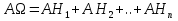 ;
;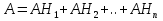 ;
; 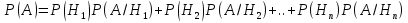 ,чтд
,чтд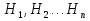 называют гипотезами.
называют гипотезами.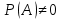 , тогда условные вероятности событий полной группы при условии наступления события A находятся по формуле Байеса:
, тогда условные вероятности событий полной группы при условии наступления события A находятся по формуле Байеса: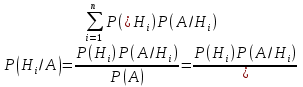
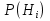 называются априорными вероятностями гипотез, а
называются априорными вероятностями гипотез, а 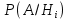 называются апостериорными вероятностями гипотез.
называются апостериорными вероятностями гипотез.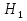 – из первой урны во вторую был переложен белый шар;
– из первой урны во вторую был переложен белый шар; 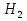 – из
– из 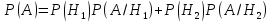 ;
;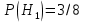 ;
;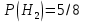 ;
;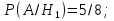
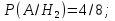
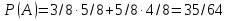
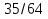
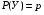 ,
, 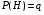 , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию.
, p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. 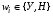 .
. 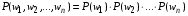 . (1)
. (1)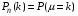 — вероятность того, что в n испытаниях произошло k успехов.
— вероятность того, что в n испытаниях произошло k успехов. 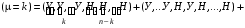
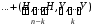 . По теореме сложения получим
. По теореме сложения получим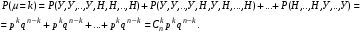 Таким образом, получим
Таким образом, получим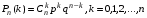 —формула Бернулли.
—формула Бернулли.
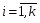 . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле:
. Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле: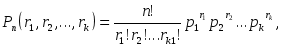 где
где 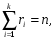
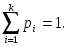
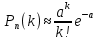 – формула Пуассона
– формула Пуассона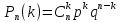 , где q=1-p.
, где q=1-p.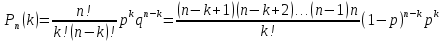
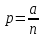
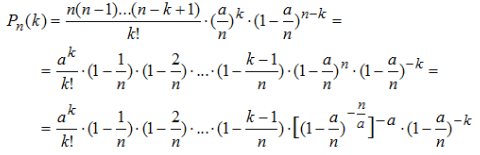
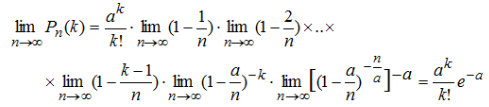
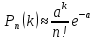 – формула Пуассона
– формула Пуассона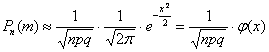 , где
, где 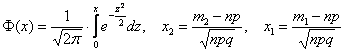
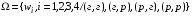 .Рассмотрим случ. величину Х–число выпадений герба на пространстве элементарных исходов Ω. Множество возможных значений случайной величины:2,1,0.
.Рассмотрим случ. величину Х–число выпадений герба на пространстве элементарных исходов Ω. Множество возможных значений случайной величины:2,1,0.