1. События и операции над ними. Относительные частоты и их свойства
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
1. События и операции над ними. Относительные частоты и их свойства Первичным понятием теории вероятностей, неопределяемым через другие понятия, является пространство элементарных исходов Ω. Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента. Примеры:1) Пусть, бросается симметричная монета. Тогда  (герб и решка). 2) Игральная кость (герб и решка). 2) Игральная кость . .Определение. Событием называется произвольное подмножество А пространства элементарных исходов Ω. Те элементарные исходы, из которых состоит событие А, называются благоприятствующими событию А. Говорят, что событие А произошло, если в результате эксперимента происходит элементарный исход w  A, т.е. благоприятствующий событию А. A, т.е. благоприятствующий событию А.Рассмотрим пример 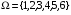 , где , где 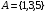 –событие, состоящее в выпадении нечетного числа очков; –событие, состоящее в выпадении нечетного числа очков; 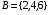 –событие, состоящее в выпадении четного числа очков. –событие, состоящее в выпадении четного числа очков.
Операции над событиями: 1) Суммой событий А и В называется объединение этих множеств А  B. B. 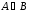 –событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В. –событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий А или В.2) Произведением событий А и В называется пересечение множеств А и В, т.е. А  В. Обозначается как АВ. АВ–событие, когда А и В происходят одновременно. 3) Разностью событий А и В называется разность множеств А\В. А\В–событие, которое происходит <=>, когда происходит А и не происходит В. 4) События А и В называются несовместимыми, если В. Обозначается как АВ. АВ–событие, когда А и В происходят одновременно. 3) Разностью событий А и В называется разность множеств А\В. А\В–событие, которое происходит <=>, когда происходит А и не происходит В. 4) События А и В называются несовместимыми, если 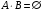 . Если А и В несовместимы, то будем обозначать . Если А и В несовместимы, то будем обозначать  . 5) Говорят, что событие А влечет событие В, если А является подмножеством В, т.е. (когда происходит А, происходит В). 6) Событие Ā=Ω\A называется противоположным к событию А. Ā происходит тогда, когда А не происходит. . 5) Говорят, что событие А влечет событие В, если А является подмножеством В, т.е. (когда происходит А, происходит В). 6) Событие Ā=Ω\A называется противоположным к событию А. Ā происходит тогда, когда А не происходит.Пусть А—некоторое событие ( 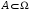 ), N(A)—число тех экспериментов, в которых произошло событие А. Тогда число ), N(A)—число тех экспериментов, в которых произошло событие А. Тогда число 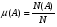 называется относительной частотой события А. Свойства относительных частот: называется относительной частотой события А. Свойства относительных частот:1) Относительная частота произвольного события А. 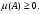 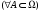 . .2) Относительная частота достоверного события равна 1. 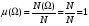 3) (Аддитивность) Относительная частота суммы несовместимых событий 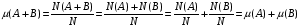 2. Аксиомы ТВ. Дискретные пространства элементарных исходов. Классическое определение вероятности. Аксиомы теории вероятностей. Пусть Ω—пространство элементарных исходов. Предположим, что F—некоторый класс подмножеств Ω.
1. 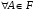 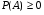 2.  , т.е. вероятность достоверного события равна 1. , т.е. вероятность достоверного события равна 1.3. (счетной аддитивности) Если 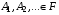 и и 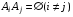 , то , то  (для несовместимых событий). (для несовместимых событий).Дискретные пространства элементарных исходов.
Все другие бесконечные множества называются несчетными. Примером несчетного множества может служить [а,b], счетного N.
Любому элементарному исходу  ставится в соответствие число ставится в соответствие число  , так что при этом , так что при этом 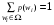 . Т.е. . Т.е. 
Сделаем следующие предположения:
Если пространство элементарных исходов конечно, а все элементарные исходы равновероятны, то вероятностью события А называется отношение числа элементарных исходов, благоприятствующих событию А к общему числу элементарных исходов: 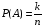 . . Это классическое определение вероятности. 3. Элементы комбинаторики. Число выборок Лемма 1. Из m элементов а1,…,аm первой группы и n элементов b1,…,bn второй группы можно составить ровно m∙n упорядоченных пар вида (аi, bj), содержащих по одному элементу из каждой группы. Лемма 2. Из n1 элементов первой группы a1, а2,…, аn1,n2 элементов второй группы b1, b2,…,bn2,n3 элементов k-ой группы x1,x2,…,xnk можно составить ровно n1∙ n2∙…∙nk различных упорядоченных комбинаций вида 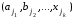 , содержащих по одному элементу из каждой группы. , содержащих по одному элементу из каждой группы.Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов 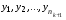 . Рассмотрим комбинацию . Рассмотрим комбинацию  как как  и и 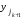 . Предположение дает возможность вычислить число комбинаций из k элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1 элементов n1 n2… nk+1. . Предположение дает возможность вычислить число комбинаций из k элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1 элементов n1 n2… nk+1.Все выборки можно классифицировать по 2 признакам: 1) упорядоченные и неупорядоченные, 2) с возвращением и без возращения. Если выборка упорядоченная, то выборки с одним и тем же составом выбранных элементов, но разным порядком элементов в выборках, считаются различными. Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элементов отождествляются.
Упорядоченная выборка с возвращением 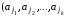 ). Каждый элемент выборки может принимать n значений, т.е. число выборок ). Каждый элемент выборки может принимать n значений, т.е. число выборок 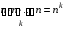 . Упорядоченная выборка без возвращения . Упорядоченная выборка без возвращения  . .Упорядоченная выборка без возвращения называется размещением. Число размещений 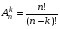 . .Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке. Pk-число перестановок из k элементов. 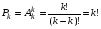 , поскольку 0!=1. , поскольку 0!=1.Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через  . .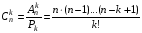 . .  , где , где 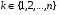 . .4. Размещения, перестановки, сочетания. Свойства сочетаний
Пример. В лифт 12-этажного дома зашли 3 человека. Найти вероятность того, что все вышли на разных этажах. 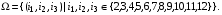 n=113. n=113.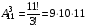 , , 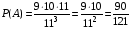 . .
Pk - число перестановок из k элементов. 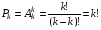 , поскольку 0!=1. , поскольку 0!=1.
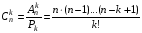 . .  , где , где  . .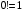 . .Свойства сочетаний: 1.  . .2.  . .3. 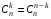 . .4.  . .5. Геометрические вероятности. Предположим, что на числовой оси имеется некоторый отрезок [a,b] и на этот отрезок наудачу бросается точка. Найти вероятность того, что эта точка попадет на 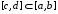 . .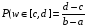 —геометрическая вероятность на прямой. —геометрическая вероятность на прямой.Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством: 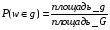 —геометрическая вероятность на плоскости. —геометрическая вероятность на плоскости.Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством: 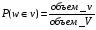 —геометрическая вероятность в пространстве. —геометрическая вероятность в пространстве.Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности. 6. Свойства вероятности Свойство 1. Вероятность невозможного события равна 0, т.е. P 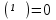 . .P  Свойство 2. Вероятность достоверного события равна 1, т.е. P  . .P 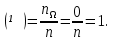 Свойство 3. Для любого события A:0≤P(A)≤1. P(A)=  , т. к. 0≤ , т. к. 0≤ то 0≤ то 0≤ ≤1 и следовательно 0≤P(A)≤1. ≤1 и следовательно 0≤P(A)≤1.Свойство 4. Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей: P(A+B)=P(A)+P(B) P(A+B)=  Свойство 5. (обобщенная теорема сложения вероятностей) P(A  B)=P(A)+P(B)-P(AB). B)=P(A)+P(B)-P(AB).P(A  B)= B)=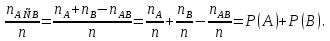 Свойство 6. (теорема сложения k слагаемых) Если события 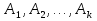 попарно несовместимы, то попарно несовместимы, тоP(  )= P( )= P(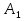 )+ P( )+ P( )+…+ P( )+…+ P(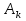 ). ).Свойство 7. Если A 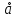 B (A влечет B), то P(A)≤P(B). B (A влечет B), то P(A)≤P(B). B=A+(B\A), тогда P(B)=P(A)+P(B\A)≥P(A). Свойство 8. Если A 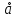 B, то P(B\A)=P(B)-P(A). B=A+(B\A). Следовательно, B, то P(B\A)=P(B)-P(A). B=A+(B\A). Следовательно, P(B)=P(A)+P(B\A). Тогда P(B\A)=P(B)-P(A). Свойство 9. P(  )=1-P(A). )=1-P(A).  = =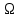 \A, P( \A, P( )=P( )=P(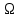 \A)=P( \A)=P(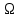 )-P(A)=1-P(A). )-P(A)=1-P(A).Свойство 10. Если события 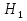 , , 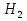 ,…, ,…, образуют полную группу, то P( образуют полную группу, то P(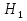 )+P( )+P(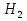 )+…+P( )+…+P( )=1. )=1.Т.к. 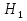 + + 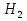 +…+ +…+ = =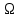 , то по свойству 6: , то по свойству 6: P(  )+P( )+P(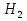 )+…+P( )+…+P( )=P( )=P( )=1. )=1.7. Условная вероятность. Независимость, независимость в совокупности Условной вероятностью события B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение 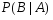 . .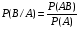 . . . .Теорема (умножение вероятностей): 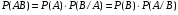 Теорема (обобщенная теорема умножения): Теорема (обобщенная теорема умножения): . .Доказательство: 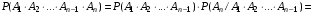  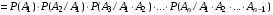 События А и В называются независимыми, если  . .Свойство. События А и В независимы тогда и только тогда, когда P(B/A)=P(B).  . .Пусть P(B/A)=P(B), тогда 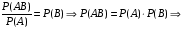 А и В независимы. А и В независимы.События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если 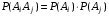 (для i≠j; i,j (для i≠j; i,j {1,2,3,…,n})–попарная независимость событий; {1,2,3,…,n})–попарная независимость событий;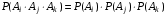 , …, , …, . .Можно показать, что из попарной независимости не вытекает независимость в совокупности. 8. Формулы полной вероятности и Байеса Теорема (Формула полной вероятности) – Если события 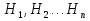 образуют полную группу, то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, равна: образуют полную группу, то вероятность появления события A, которое может произойти совместно с любым из событий полной группы, равна: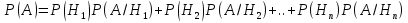  |

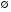 (т.е. множество, которое не содержит ни одного элементарного исхода) называется невозможным событием, поскольку оно никогда не происходит.
(т.е. множество, которое не содержит ни одного элементарного исхода) называется невозможным событием, поскольку оно никогда не происходит. ставится в соответствие действительное число P(A), называемое вероятностью А, так что при этом выполняется аксиомы:
ставится в соответствие действительное число P(A), называемое вероятностью А, так что при этом выполняется аксиомы: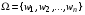 или
или 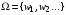 .
.  .
.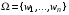 —конечно.
—конечно.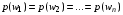 . Тогда получим
. Тогда получим  , т.к. слагаемые равны, то имеем
, т.к. слагаемые равны, то имеем 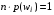 , т.е.
, т.е. 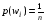 , где
, где 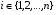 . Рассмотрим некоторые события
. Рассмотрим некоторые события 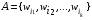 , где k≤n. Вероятность события A.
, где k≤n. Вероятность события A. 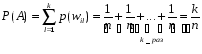


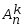
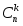
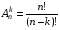 .
.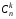 .
.