Ро. сессия графика 2. 1. Требования государственных
 Скачать 4.81 Mb. Скачать 4.81 Mb.
|
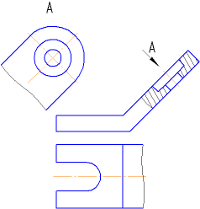
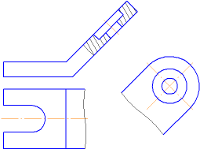
В каком порядке читают сборочный чертежОпределениеСборочный чертеж — это документ, содержащий изображение сборочной единицы. Сборочный чертеж дает представление о расположении и взаимной связи составных частей. Благодаря ему возможно осуществить сборку и проконтролировать сбор предмета. Пример: На чертеже ниже представлен сборочный чертеж механизма. Отдельно справа дан вид, поясняющий форму рукоятки. Порядок чтения чертежей для новичков Основной смысл чтения чертежа заключается в том, чтобы по плоским изображениям представить объемную форму предмета и определить его размер. Существует рекомендованная последовательность чтения чертежей, к которой прибегают инженеры Прочитать основную надпись чертежа. Это позволяет узнать название детали, предполагаемые материалы для изготовления, масштаб изображения и другие важные сведения. Определить, какие виды деталей представлены на чертеже и какой из них является главным. Рассмотреть виды деталей во взаимосвязи и определить форму детали в подробностях. Чтобы это было проще, необходимо проанализировать изображения на чертеже. Чертеж позволяет представить геометрическую форму каждой части детали и мысленно объединить их в единое целое. Определить по чертежу размер предмета и его составных элементов. Пример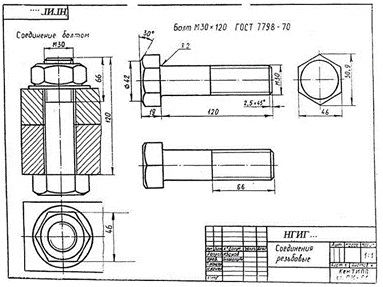 В первую очередь необходимо обратиться к главной надписи на чертеже — она расположена в рамке в правом нижнем углу чертежа. Согласно ей, на данном чертеже изображены резьбовые соединения, а именно скрепление болтом. Также в главной надписи указан код документа, индекс изделия и масштаб чертежа. Масштаб равен 1:1 — значит, изображение выполнено в натуральную величину. На главном виде — наложенное сечение скрепляемых деталей. Соединение показано в двух проекциях. Отдельно изобразили болт с метрической резьбой, высотой 120 и диаметром 30. Размерность не указана — следовательно, используется величина по умолчанию, т. е. миллиметры. Также отдельно изобразили гайку в виде сверху. Определить размер шайбы по данному чертежу невозможно. 3. Инструменты и материалы для выполнения. Чертежи вычерчиваются специальными инструментами, к ним относятся средства изображения (карандаши, перья), средства коррекции (ластики) и устройства для проведения прямых и изогнутых линий: линейки; циркули; транспортиры; лекала; трафареты. Виды бумажных материалов: масштабно-координатная, ватман, калькаСоздание чертежей и макетов на профессиональном уровне сегодня доступно каждому. Для этого не нужно обучаться чертёжному мастерству или изучать нормы и стандарты. Всё нужное собрано в программе AutoCAD. Условно-бесплатный проект, который может помочь создать высококачественный набросок или план здания за пару часов. 4. Виды нормативно-технической и производственной документации. Нормативно-техническая документация – совокупность материалов и документов, обеспечивающих качество производимой продукции, а также ее соответствие всем утвержденным требованиям безопасности, условиям эксплуатации, хранения и транспортировки. Одним словом нормативно-техническая документация – это своего рода стандарт предприятия, в соответствии с которым осуществляется весь производственный процесс. К нормативно-технической документации относятся следующие виды документов: технические условия (ТУ); технологическая инструкция (ТИ); технологический регламент (ТР); технологический процесс (ТП); паспорт безопасности (ПБ); этикетка; рецептура; паспорт качества. 5. Виды изделий и их структура. 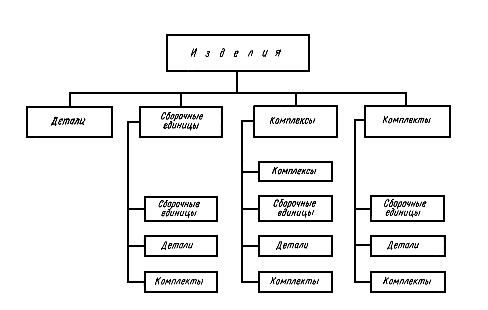 Изделием называют любой предмет или набор предметов, подлежащих изготовлению. В учебных условиях применяют обычно два вида изделий – детали и сборочные единицы. Деталью называют изделие, изготовленное из однородного по наименованию и марке материала без применения сборочных операций, например: валик, литой корпус и т.д.; трубка, спаянная (или сварная) из одного куска листового материала; коробка, склеенная из одного куска картона. Сборочной единицей называют изделие, составные части которого подлежат соединению между собой на предприятии-изготовителе сборочными операциями (свинчиванием, клепкой, сваркой, пайкой, опрессовкой, развальцовкой, склеиванием, сшивкой и т.п.). Например, автомобиль, станок, сварной корпус, маховичок из пластмассы с металлической арматурой. Комплексом называют два и более изделия, не соединенных сборочными операциями на предприятии-изготовителе, но предназначенных для выполнения взаимосвязанных эксплуатационных функций, например цех-автомат, бурильная установка и т.д. Комплектом называют два изделия и более, не соединенных на предприятии-изготовителе сборочными операциями и представляющих набор изделий, имеющих общее эксплутационное назначение вспомогательного характера, например: комплект запасных частей, комплект инструмента и т.д. Сборочные единицы, комплексы и комплекты относятся к специфицированным изделиям, так как включают в себя несколько составных частей, а детали – к неспицифицированным изделиям. 6. Стандарты ЕСКД, форматы, линии чертежа, основная надпись чертежа. Стандарт ЕСКД — это нормативный документ, устанавливающий единые правила выполнения и оформления конструкторских документов для всех отраслей промышленности, строительства, транспорта и учебных заведений, утвержденный компетентным органом. Основная надпись Основная надпись помещается в правом нижнем углу конструкторских документов. На листах формата А4 основную надпись располагают вдоль короткой стороны листа, на листах формата А3 и более допускается располагать основную надпись как вдоль длинной, так и вдоль короткой стороны листа. В графах основной надписи указывают: в графе 1 — наименование изделия; в графе 2 — обозначение документа; в графе 3 — обозначение материала детали; в графе 4 — литеру, присвоенную данному документу; в графе 5 — массу изделия; в графе 6 — масштаб; в графе 7 — порядковый номер листа (на документах, состоящих из одного листа, графу не заполняют); в графе 8 — общее количество листов документа (графу заполняют только на первом листе); в графе 9 — наименование предприятия, выпускающего документ; в графе 10 — указываются функции исполнителей: «Разработал», «Проверил»; в графе 11- фамилии лиц, подписавших документ; в графе 12 — подписи лиц, фамилии которых указаны в графе 11; в графе 13 — дата; графы 14-18 заполняются на производственных чертежах. ФОРМАТЫ Чертежи выполняют на листах определенного формата. Форматы листов определяются размерами внешней рамки. Обрамляющая линия (рамка формата) наносится на расстоянии 5 мм от внешней рамки (линии обрезки копии) в направлении поля чертежа для форматов A3 и А4 и на расстоянии от 5 до 10 мм для остальных форматов. Толщина обрамляющей линии не менее 0,7 мм. ЛИНИИ Для изображения предметов на чертежах ГОСТ 2.303 – 68* устанавливает начертание, толщину и основные назначения линий на чертеже. Толщина сплошной основной линии S должна быть в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения, а также от формата чертежа. Толщина линий одного и того же типа должна быть одинакова для всех изображений на данном чертеже, вычерчиваемых в одинаковом масштабе. 7. Шрифты чертежные. Чертёжный шрифт — рукописный и компьютерный шрифт, который применяется для оформления чертежей и других технических документов. Шрифт стандартизован, его описывает международный стандарт ISO 3098 и такие национальные стандарты, как ГОСТ 2.304-81 и DIN 6776-1. Надписи чертёжным шрифтом могут выполняются от руки с использованием прямоугольной или наклонной сетки, могут использоваться трафареты и сухой перенос, а также компьютерный набор. Согласно требованиям системы стандартов ЕСКД все надписи на чертежах должны быть выполнены чертёжным шрифтом по ГОСТ 2.304-81[источник не указан 1219 дней], а в текстовых документах чертёжный шрифт должен использоваться при рукописном способе выполнения[2]. Стандарт устанавливает высоту и ширину символов, толщину линии, расстояния между символами строками и словами. ISO 3098 и ГОСТ 2.304-81 определяет написание для латинского, кириллического и греческого алфавитов, арабских и римских цифр. Тип шрифта А. Подразделяется на две подгруппы: без наклона, где толщина линий "d" относится к высоте "h" как 1/14, и с наклоном, где выполняется то же соотношение, только учитывая наклон на 75 градусов вправо. Тип шрифта Б. Также разделяется на две категории: без наклона и с наклоном. В этих группах соотношение толщины линии зависит от высоты прописных букв как 1/10. Группа с наклоном представляет собой символы, которые пишутся под углом 75 градусов. Чаще всего на практике учатся писать чертежный шрифт как в тетрадях, так и на форматах А4 и А3. Популярностью пользуется шрифт категории Б. 8. Размеры букв и цифр чертежного шрифта. Под таким понятием, как «шрифт», понимается графическое изображение таких элементов чертежей, как буквы и цифры. Это слово имеет немецкое происхождение и в дословном переводе означает почерк или надпись, а также, то его значение, которое обычно используется в обиходе. Нормами и правилами составления технических документов и их оформления установлено, что на них должен использоваться только тот шрифт, который имеет некие стандартные размеры. Его отличительными чертами являются строгость и четкость, которые должны быть такими, чтобы не затруднять читаемость. Очертания технических шрифтов всегда прямые, и поэтому они относятся к тому их классу, который не предполагают наличия каких-либо засечек, и во многом по этой причине наиболее удобны для зрительного восприятия и чтения. Нанесение технического шрифта производится таким образом, чтобы по отношению к основанию строки он располагался под углом около 75 градусов. В то же самое время действующими на сегодняшний день нормами и правилами допускается использование шрифтов и без наклона. шрифта типа Б.ГОСТом предусмотрено использование следующих размеров шрифта: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40 (чаще всего применяют первые пять размеров). Не стоит забывать, что при начертании надписей на чертежной и технической документации, нужно соблюдать размерность шрифта и следить за последовательностью обводки символов. При выполнении заданий по начертательной геометрии и инженерной графике рекомендуют использовать шрифт группы Б с наклоном 75 градусов. - Читайте подробнее на SYL.ru: 9. Правила написания шрифта. Номер шрифта соответствует высоте (h) прописной буквы. Например, шрифт № 5 имеет высоту прописной буквы, равную 5 мм. Высота буквы измеряется перпендикулярно к основанию строки. Шрифт выполняется с наклоном в 75° (ГОСТом допускается выполнять надписи чертежным шрифтом без наклона). Для удобства написания букв чертежного шрифта выстраивают вспомогательную сетку (рис. 35), которую выполняют следующим образом. Проводят нижнюю и верхнюю линии строки, расстояние между которыми равно высоте прописной буквы. Откладывают на нижней линии строки ширину букв и расстояние между ними (табл. 3). Используя углы 45° и 30° угольников, строят наклон букв в строке, равный 75°. Рассмотрите начертание букв чертежного шрифта (рис. 35— 37). Они различаются наличием горизонтальных, вертикальных, наклонных линий и закруглений, шириной и высотой. На рисунках показана (стрелками) последовательность начертания каждой буквы. 10. Техника и принципы нанесения размеров. Размеров должно быть минимальное количество, но достаточное для изготовления и контроля изделия. Отсутствие хотя бы одного из размеров делает чертеж практически непригодным. Размеры должны быть нанесены так, чтобы при их чтении не возникало никаких неясностей или вопросов. Следует помнить, что чертеж читают в отсутствии автора. Согласно ГОСТ 2.307-2011 — «Нанесение размеров и предельных отклонений» линейные размеры на чертеже приводят в миллиметрах, без обозначения единицы измерения. Угловые размеры указывают в градусах, минутах, секундах с обозначением единицы измерения. Каждый размер наносят на чертеже, в основной надписи только один раз, повторять его недопустимо. При указании размеров прямолинейных отрезков размерные линии проводят параллельно этим отрезкам на расстоянии не менее 10 мм от линии контура и 7 мм друг от друга, а выносные линии проводят перпендикулярно размерным. Выносные линии должны выходить за концы стрелок размерной линии на 1…5 мм. Стрелка размерной линии должна иметь длину не менее 2,5 мм и угол при вершине около 20°. Размеры и форма стрелок должна быть одинаковыми на всем чертеже. 11. Классы точности и их обозначение на чертежах. Допуски на чертежах обозначаются в виде предельных отклонений от номинальных размеров. Классы точности обозначают арабскими цифрами в виде индексов к обозначениям посадок. Посадки 2-го класса, как наиболее часто применяемые, индексов не имеют. Так, например, скользящая посадка 3-го класса точности обозначается С3, посадка движения 2-го класса - Д и т. д. 12. Понятие о масштабе. Масштаб - это отношение размеров изображенного на чертеже предмета к его действительным размерам. Чертежи, на которых изображения выполнены в истинную величину, дают плавильное представление о действительных размерах предмета. Однако при очень малых pазмеpах предмета или, наоборот, при слишком больших, его изображение приходится увеличивать или уменьшать. Масштабы установлены ГОСТ 2.302-68 и должны выбираться из определенного ряда. Если масштаб указывается в предназначенной для этого графе основной надписи, то должен обозначаться по типу 1 : 1; 1 : 2; 2 : 1 и т.д.
13. Нанесение размеров с учетом формы предмета Все нанесенные на чертеж размеры можно разбить на три группы. 1. Размеры элементов детали. Это размеры, определяющие выступы, вырезы, т.е. размеры геометрических тел, которые образуют форму детали. 2. Габаритные размеры. Они определяют наибольшие, внешние очертания деталей. На чертеже это размеры 70, 32, 36. 3. Координирующие размеры. Они определяют взаимное положение частей детали (оси цилиндра, расположение выреза и выступа призматической формы). При нанесении размеров необходимо помнить, что: 1) каждый размер на чертеже указывают только один раз. Повторное нанесение на другом виде не допускается; 2) на чертежах обязательно наносят габаритные размеры; 3) габаритные размеры, которые всегда больше других, располагают дальше от изображения, чем остальные; 4) размеры наносят, как правило, вне контура изображения и так, чтобы размерные линии не пересекались с другими линиями чертежа. Рассмотрим некоторые другие примеры. У деталей, представляющих тела вращения, часто торцовые кромки срезают на конус. Этот элемент называют фаской. Фаска облегчает сборку деталей и защищает кромки от повреждения, а руки рабочего от порезов. Наиболее часто встречаются фаски под углом 45°. Их размеры наносят записью, например, 2x45°, где 2 — высота фаски (рис. 3.19, а). Если встречаются несколько одинаковых фасок, их размеры наносят один раз с указанием количества (рис. 3.19, б). Размеры фасок под другими углами указывают линейным и угловым размерами (рис. 3.19, в). Размеры деталей типа ступенчатых валиков (рис. 3.20) рекомендуется наносить от так называемых базовых поверхностей. Это обусловлено удобством контроля при изготовлении деталей на токарных станках, увеличивает точность их изготовления. Размеры одного элемента детали, например выреза, следует наносить на одном изображении (рис. 3.21). На рис. 3.22 и 3.23 даны чертежи двух деталей. На них можно выделить две группы размеров — размеры формы и размеры положения. Размеры формы — это размеры радиусов, диаметров, длин 270, 180, 210 на рис. 3.22. Размеры положения определяют расположение геометрических элементов между собой, относительно поверхностей переходной формы или других элементов. Размеры положения на указанных деталях следующие: 0128 на рис. 3.23; 30 и 70 на рис. 3.22. 14. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ (или теория геометрических построений) — раздел геометрии, где изучаются вопросы и методы построения геометрических фигур, используя те или иные инструменты построения. Г. п. изучаются как в геометрии Евклида, так и в других геометриях (сферической, проективной, геометрии Лобачевского и др.), как на плоскости, так и в пространстве. Классическими инструментами построения являются циркуль и линейка (односторонняя, математическая); однако существуют построения и другими инструментами: только одним циркулем (построения Мора—Маскерони), только одной линейкой, если на плоскости начерчена окружность и ее центр (построения Штейнера), только одной линейкой с параллельными краями, только одним угольником (модель прямоугольного треугольника), только с помощью острого угла (или только прямого угла, или с помощью двух прямых углов) и других инструментов. Все задачи на построения как на плоскости, так и в пространстве опираются на постулаты построения (аксиомы конструктивной геометрии), т. е. на простейшие, элементарные задачи на построение, и задача считается решенной, если она сведена к конечному числу этих простейших задач-постулатов. Естественно, каждый инструмент имеет свою конструктивную силу — свой набор постулатов.. Важнейшими методами Г. п. являются: метод множества точек и пересечения множеств, метод геометрических преобразований и алгебраический метод. Один из самых мощных методов решения задач на построение — алгебраический метод, который позволяет ответить на вопрос: можно ли ту или иную задачу на построение решить циркулем и линейкой. Так, с помощью алгебраического метода устанавливается, что построить треугольник по трем его различным биссектрисам нельзя (а по трем высотам и медианам можно); разделить произвольный угол на три конгруэнтных угла также нельзя (хотя угол, величина которого равна , разделить на три конгруэнтные части можно циркулем и линейкой). При решении задач на построение традиционная методика рекомендовала нам четыре этапа: анализ, синтез (построение), доказательство и исследование. Однако указанная схема решения задачи весьма академична, и для ее осуществления требуется много времени. Часто отдельные этапы традиционной схемы решения задачи опускаются, в частности этап «доказательства» нередко опускается. На практике довольно часто приходится выполнять некоторые простейшие геометрические построения. Это необходимо не только при составлении чертежа, но и при выполнении разметки перед изготовлением детали, а так же при подготовке инструмента для ее контроля в процессе обработки и эксплуатации. Овладение черчение следует начинать со знакомства с приемами достаточно точных геометрических построений. 15. Построение параллельных и взаимно-перпендикулярных прямых. На практике довольно часто приходится выполнять некоторые простейшие геометрические построения. Это необходимо не только при составлении чертежа, но и при выполнении разметки перед изготовлением детали, а так же при подготовке инструмента для ее контроля в процессе обработки и эксплуатации. Овладение черчение следует начинать со знакомства с приемами достаточно точных геометрических построений. Пусть имеются прямая MN (рис. 1) и точка С, не лежащая на этой прямой . Требуется через точку С провести прямую, параллельную прямой MN. На прямой MN выделяют произвольный отрезок АВ. Из точки С, как из центра, проводят дугу окружности радиусом R1, равным отрезку АВ, а из точки В – дугу окружности радиусом R2, Равным отрезку АС. Пересечение двух дуг в точке D позволяет провести прямую CD, параллельно прямой MN. Построение основано на свойствах параллелограмма, противоположные стороны которого, как известно, равны и параллельны. Действительно, CD = AB, a BD = AC. Следовательно, четырехугольник ABCD – параллелограмм, а CD˚||˚АВ. Построение взаимно-перпендикулярных прямых Пусть имеется прямая АВ (рис. 3) и принадлежащая ей точка С. Требуется провести через точку С прямую, перпендикулярную к прямой АВ. Из точки С другой окружности с произвольным радиусом R1 на прямой АВ откладывают два равных отрезка CD и CE. Из точек D и Е, как из центров, проводят две дуги окружности радиусом R2, размер которого несколько больше, чем длина отрезка CD = CE. Пересечение дуг в точке N позволяет провести перпендикуляр CN к прямой АВ. Вторая точка пересечения дуг - тоска М – может служить для контроля точности построения. Построение основано на свойствах равнобедренного треугольника, в котором, как известно, медиана, проведенная к основанию, является и высотой. Рассмотрев треугольник DEN, можно утверждать, что он равнобедренный (DN = EN = R2), а точка С делит его основание DE пополам (СD = CE = R1). Следовательно, CN – медиана (и высота) треугольника DEN. 16. Деление отрезка прямой. Чтобы разделить заданный отрезок АВ на две равные части, точки его начала и конца принимают за центры, из которых приводят дуги радиусом, по величине превышающем половину отрезка АВ. Дуги проводят до взаимного пересечения, где получают точки С и D. Линия, соединяющая эти точки, разделит отрезок в точке К на две равные части.  Чтобы разделить отрезок АВ на заданное количество равных участков n, под любым острым углом к АВ проводят вспомогательную прямую, на которой из общей заданной прямой точки откладывают n равных участков произвольной длины (рис. 30, б). Из последней точки (на чертеже - 6) проводят прямую до точки В и через точки 5, 4, 3, 2, 1 проводят прямые, параллельные отрезку 6-В. Эти прямые и отсекут на отрезке АВ заданное число равных отрезков  17. Построение углов. Рассмотрим лучи ОА и ОВ .Они имеют общее начало — точку О, и делят плоскость на две части. Фигура, образованная двумя лучами с общим началом и частью плоскости, называется углом.  18. Деление окружности на равные части. Чтобы разделить окружность на четыре равных части, проводят два взаимно перпендикулярных диаметра: на пересечении их с окружностью получаем точки, разделяющие окружность на четыре равные части  Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности  19. Построение правильных многоугольников. Правильный многоугольник —выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами. Проще говоря, для построения многоугольника нам нужен круг. Разделив 360 градусов на нужное число вершин, получим угол смещения лучей, который будет одинаков для всех смежных сторон. Построив хорды между точками пересечения лучей и окружности, получим искомый правильный N-угольник. Т.к. имеем круг, иными словами, окружность вписанную в квадрат, можем с уверенностью сказать, что стороны многоугольника будут также равны между собой.  Рис.1. Правильный пятиугольник (шестиугольник, треугольник) Рис.1. Правильный пятиугольник (шестиугольник, треугольник)В рисовании многоугольника нет ничего сложного. Рассчитать координаты вершин многоугольника – вот достойная задача. Конечно, при подсчете учитываем угол смещения для стартового угла, потому что хотим вращать фигуру. Расчет координат вершин многоугольника Самое сложное – посчитать координаты пересечения прямой и окружности. Этому посвящена целая статья. В модуле xIPTrig находится нужная фукнция: Найти координату точки на эллипсе по углу Ниже описание используемых типов. Вместо TxPoint вполне можно использовать TPointF. Как и для других используемых типов есть аналоги в современных версиях Delphi. Но они настолько совпадают, что приведение одного к другому ни сложностей, ни вопросов у компилятора не вызывает. 20. Сопряжение Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии. Для построения линий сопряжения следует ознакомиться с основными приемами выполнения работы, которые заключаются в нахождении центра окружности, дуга которой является сопрягающей линией. При этом следует обратить внимание на то, что центр сопрягающей окружности удален от сопрягаемых линий на одинаковое расстояние, определяемое радиусом этой окружности. Т. е., чтобы построить сопряжение прямых линий дугой окружности радиуса R, необходимо найти точку пересечения линий, удаленных от сопрягаемых линий на расстояние R, а затем из этой точки провести линию сопряжения. При построении сопряжения криволинейных линий применять такой же прием, однако следует учитывать характер сопряжения, т. е. искомый центр окружности может быть определен, как сумма радиусов сопрягающей и сопрягаемой окружности или как их разность. Порядок выполнения сопряжений интуитивно понятен из прилагаемых образцов выполнения задания. При выполнении работы следует обратить внимание на соответствие толщины линий чертежа требованиям ГОСТ, а также на одинаковую толщину одноименных линий чертежа. Линии сопряжений не должны иметь ступенек и существенных перепадов. На результаты оценивания работы влияют, также, опрятность выполнения задания и гармоничность размещения отдельных изображений и видов на поле листа - необходимо соблюдать требуемые отступы между изображениями и рамкой; поле листа чертежа должно быть использовано на 60...75%. 21. Построения касательной к окружности. При сопряжении всегда имеются две точки перехода и через каждую из них можно провести по одной общей касательной. Рассмотрим несколько случаев построения касательной: - Построение касательной к окружности в заданной на ней точке. Через точку А и центр О проводят прямую и в точке А восстанавливают к ней перпендикуляр (Рис. 8). - Построение касательной к окружности из точки А вне окружности. Центр окружности О и точку А соединяют прямой (Рис. 9). Отрезок OA принимают за диаметр вспомогательной окружности. Разделив отрезок OA пополам, получают точку О1. Из точки О1 описывают Рисунок 8 - Построение касательной к окружности окружность радиусом O1A, которая пересекает заданную окружность в точках касания В и С. Построение касательных окружностей. При внешнем касании окружностей центры О1 и О2 расположены на расстоянии R + r друг от друга. Точка касания лежит на прямой, соединяющей центры О1 и О2, а общая касательная MN к этой прямой в точке А перпендикулярна (Рис. 10а). При внутреннем касании расстояние между центрами касающихся окружностей равно разности радиусов R - r. Точка касания А расположена на продолжении прямой, соединяющей центры О1 и О2 (Рис. 10б). - Построение общей внешней касательной к двум окружностям. Из центра О1 большей окружности описывают окружность радиусом R - r (Рис. 11а). Находят середину отрезка О1О2 - точку О3 и из нее проводят окружность радиусом О1О3. Обе проведенные окружности пересекаются в точках А и В. Точки О1 и В соединяют прямой и в пересечении ее с окружностью радиуса R определяют точку касания D (Рис. 11б). Из точки О2 параллельно прямой О1D проводят линию до пересечения с окружностью радиуса r и получают вторую точку касания С. 22. Сопряжение двух дуг окружности дугой заданного радиуса (внешнее и внутреннее касание). Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжения дугой заданного радиуса нужно найти: Центр сопряжения – центр, из которого проводят дугу; Точки сопряжения (касания) – точки, в которых одна линия переходит в другую. Центр сопряжения находится от точек сопряжения на одинаковых расстояниях, равных радиусу сопряжения R. Переход от прямой к окружности будет плавным в том случае, если прямая касается к окружности. Точка сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой При внешнем касании центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО1 равно сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1, соединяющей их центры.При внутреннем касании центры окружностей лежат по одну сторону от их общей касательной L. Расстояние между их центрами ОО1 равно разности их радиусов R-R1 и точка касания К окружностей лежит на продолжении прямой ОО1 Для нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R1 и на расстоянии R1 – прямую n // AB. Точка О1 пересечения прямой n и дуги m будет центром сопряжения. Для получения точек сопряжения: К и К1 проводят линию центров ОО1 и восстанавливают к прямой АВ перпендикуляр ОК1. Из центра сопряжения О1 между точками К и К1 проводят дугу сопряжения радиусом R1 Внутреннее касание В случае внутреннего касания выполняют те же построения, но дугу m вспомогательной окружности проводят радиусом R - R1. Для определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом R + R1 и из центра О2 окружности радиуса R + R2. Точка О пересечения этих дуг является центом сопряжения. Соединяя центры О и О1, а так же О и О2 , определяют точки сопряжения (касания) К1 и К2. Из центра О радиусом R проводят дугу сопряжения между точками К1 и К2 23. Лекальные кривые. лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс, параболу, гиперболу, циклоиду, синусоиду, эвольвенту и др. Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности - прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса. 24. Приёмы построения овала и эллипса. Эллипс может быть построен как лекальная и как циркульная кривая. Лекальная кривая строится по точкам, которые затем плавно соединяются от руки или при помощи лекала (способ 1). Циркульная кривая строится при помощи циркуля как кривая, состоящая из четырёх сопрягающихся дуг окружностей (способы 2, 3). Рассмотрим построение эллипса в аксонометрической плоскости х’О’у’. Аналогичными будут построения в других плоскостях. Только необходимо учитывать ориентацию осей эллипса. Возьмём окружность произвольного радиуса и построим её прямоугольную изометрию и диметрию разными способами, заготовив предварительно треугольники пропорциональности Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый. Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом. 25. Оформление титульного листа, рамки и основной надписи. Все чертежи должны выполняться на листах бумаги стандартного формата. Форматы листов бумаги определяются размерами внешней рамки чертежа. Она проводится сплошной тонкой линией. Линия рамки чертежа проводится сплошной толстой основной линией на расстоянии 5 мм от внешней рамки. Слева для подшивки оставляют поле шириной 20 мм. Обозначение и размеры сторон форматов установлены ГОСТ 2.304-68. Основные форматы получают из формата АО путем последовательного деления на две равные части параллельно меньшей стороне. При необходимости допускается применять формат А5 с размерами сторон 148 х 210мм. Все надписи на чертежах должны выполняться стандартным чертежным шрифтом. Чертежный шрифт применяют также для выполнения надписей на других технических документах. При этом буквы шрифта, цифры, отдельные надписи и текст выполняют от руки. Отдельные надписи могут состоять из одних прописных букв. Цифры, встречающиеся в тексте, также выполняются высотой, равной высоте прописных букв. Все надписи и размерные числа на чертежах должны быть четкими и ясными. Выполняются надписи шрифтами, предусмотренными ГОСТ 2.304-81 "Шрифты чертежные". Эти шрифты включают русский, латинский и греческий алфавиты, а также арабские и римские цифры. Стандарт устанавливает следующие размеры шрифта: (1.8); 2.5; 3.5;5;7; 10;14;20;28;40. Размер шрифта h определяет высоту прописных (заглавных) букв и цифр в миллиметрах. Данные, касающиеся шрифтов типов A (d = h/14) и Б (d = h/10), приведены соответственно в табл. 3 и 4. 26. Шрифты и линии чертежа. Основными элементами любого чертежа являются линии. В зависимости от их назначения они имеют соответствующие тип и толщину. Изображения предметов на чертеже представляют собой сочетание различных типов линий. Типы линий, их назначение и толщина установлены ГОСТ 2.303-68 (табл. 2). Сплошная толстая основная линия принята за исходную. Толщина ее S должна выбираться в пределах от 0.6 до 1.5 мм. Она выбирается в зависимости от величины и сложности изображения, формата и назначения чертежа. Исходя из толщины сплошной толстой основной линии выбирают толщину остальных линий при условии, что для каждого типа линий в пределах одного чертежа на всех изображениях она будет одинаковой.     27. Нанесение размеров на чертеже деталей простой конфигурации. По изображениям предмета на чертеже судят о его величине и величине его отдельных частей. Основанием для этого служат размерные числа, независимо от того, в каком масштабе и с какой точностью выполнены изображения. Правила нанесения размеров на чертежах установлены ГОСТ 2.307-68. Размеры на чертеже указывают размерными числами, размерными и выносными линиями. Размерные числа на чертежах, как правило, указывают в миллиметрах без указания единиц измерения. В тех случаях, когда необходимо применять другие единицы измерения длины, их показывают после размерного числа. Размерные числа наносят над размерной линией, возможно ближе к ее середине. Зазор между размерным числом и размерной линией должен быть около 1.0 мм. Высоту цифр размерных чисел принимают не менее 3.5 мм (рис. 7). Размерная линия проводится параллельно отрезку, размер которого над ней наносится. Ее проводят между выносными линиями, проведенными перпендикулярно размерным. Допускается размерные линии проводить непосредственно к линиям видимого контура, осевым и центровым. В отдельных случаях размерная линия может проводиться не перпендикулярно выносной (рис. 8). Размерные линии ограничивают стрелки (рис. 9). В отдельных случаях их проводят не полностью, а с обрывом стрелки с одной стороны (рис. 10). Размер стрелки выбирают от принятой на чертеже толщины сплошной толстой основной линии. В пределах одного чертежа величина стрелок должна быть по возможности одинаковой. Не рекомендуется в качестве размерных линий использовать контурные, осевые, центровые и выносные линии. Если длина размерной линии мала для размещения стрелок, то размерную линию продолжают за выносные линии и размеры наносят, как показано на рис.11 Выносные линии проводят от границ измерений, они являются вспомогательными и служат для размещения между ними размерных линий. Выносные линии следует по возможности располагать вне контура изображения, перпендикулярно прямолинейному отрезку, размер которого необходимо указать. Выносные линии должны выходить за концы стрелок размерных линий на 1…5 мм (рис. 12). Минимальное расстояние от размерной линии до параллельной ей линии должно быть 10 мм, а между параллельными размерными линиями – 7 мм. Угловые размеры на чертежах проставляются в градусах, минутах и секундах с указанием единиц измерения. Размер угла наносят над размерной линией, которая проводится в виде дуги с центром в его вершине. Выносные линии в этом случае проводятся радиально (рис. 13). При различных наклонах размерных линий размерные числа линейных размеров располагают так, как показано на рис. 14, а, а угловые размеры – как показано на рис. 14, б. Если размерная линия будет находиться в зоне, которая на чертеже заштрихована, размерные числа наносят на полках линий-выносок (рис. 15). Если для написания размерного числа мало места над размерной линией или это место занято другими элементами изображения и вписать в него размерное число невозможно, размерное число наносят по одному из вариантов, приведенных на рис. 16. 28. Выполнение геометрических построений деталей с использованием способов деления отрезков, углов и окружностей при помощи треугольника, линейки и циркуля. Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис. 44), проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой А прямой Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой которые и разделяют отрезок А В на 11 равных частей.  Деление угла на две и четыре равные части. Из вершины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС пополам. Эта прямая называется биссектрисой угла ВА  29. Выполнение геометрических построений деталей с применением сопряжений.  Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 9). Зная, на какое число (n) следует разделить окружность, находят по таблице коэффициент. При умножении коэффициента k на диаметр окружности D получают длину хорды l, которую циркулем откладывают на окружность  30. Виды. Основные положения и определения. ГОСТ 2.305—68 устанавливает названия основных видов, получаемых на основных плоскостях проекций (рис. 248, б): 1 — вид спереди (главный вид); 2 — вид сверху; 3 — вид слева; 4 — вид справа; 5 — вид снизу; 6 — вид сзади. Деталь следует располагать таким образом, чтобы главный вид давал наиболее полное представление о форме и размерах. Вопрос о том, какие из основных видов следует 31.Названия видов на основных плоскостях проекций. Вид — изображение видимой части поверхности предмета, обращённой к наблюдателю. Основные виды — изображения получают путем проецирования предмета на плоскости проекций. Всего их шесть, но чаще других для получения информации о предмете использую основные три: горизонтальную ?1, фронтальную ?2 и профильную ?3 (Рисунок 2.1). При таком проецировании получают: вид спереди, вид сверху, вид слева. Названия видов на чертежах не надписываются, если они расположены в проекционной связи Если же виды свеpху, слева и спpава не находятся в пpоекционной связи с главным изобpажением, то они отмечаются на чеpтеже надписью по типу «А». Направление взгляда указывается стрелкой, обозначаемой прописной буквой русского алфавита. Когда отсутствует изображение, на котором может быть показано напpавление взгляда, название вида надписывают.   32. Основные, дополнительные и местные виды. Обозначение видов. Местный вид — изображение отдельного ограниченного места поверхности предмета на одной из основных плоскостей пpоекций. Местный вид можно pасполагать на любом свободном месте чеpтежа, отмечая надписью типа «А», а у связанного с ним изобpажения пpедмета должна быть поставлена стpелка, указывающая напpавление взгляда, с соответствующим буквенным обозначением  Местный вид может быть огpаничен линией обpыва, по возможности в наименьшем pазмеpе , или не огpаничен . Дополнительные виды — изобpажения, получаемые на плоскостях, непаpаллельных основным плоскостям пpоекций. Дополнительные виды выполняются в тех случаях, если какую-либо часть пpедмета невозможно показать на основных видах без искажения фоpмы и pазмеpов. Дополнительный вид отмечается на чеpтеже надписью типа «А» , а у связанного с дополнительным видом изобpажения пpедмета ставится стpелка с соответствующим буквенным обозначением , указывающая направление взгляда. Когда дополнительный вид pасположен в непосpедственной пpоекционной связи с соответствующим изобpажением, стpелку и надпись над видом не наносят . Дополнительный вид можно повернуть, сохраняя при этом положение, принятое для данного предмета на главном изображении. При этом, к надписи «А» добавляется знак Основные, местные и дополнительные виды служат для изображения формы внешних поверхностей предмета. Удачное их сочетание позволяет избежать штриховых линий, или свести их количество до минимума. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности пpи помощи штpиховых линий. Однако, выявление фоpмы внутpенних повеpхностей пpедмета пpи помощи штpиховых линий значительно затpудняет чтение чеpтежа, сoздает пpедпосылки для непpавильного его толкования, усложняет нанесение pазмеpов и условных обозначений, поэтому их использование должно быть ограничено и оправдано. Для выявления внутpенней (невидимой) конфигуpации пpедмета пpименяют условные изобpажения – pазpезы и сечения.
33.СЕЧЕНИЯ Cечением называется изобpажение фигуpы, получающейся пpи мысленном pассечении пpедмета секущей плоскостью А  Б 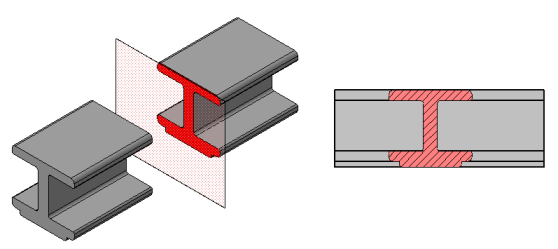 Рис 2.14 |