РГР. РГР 2020. 1 Задача Оценка согласованности мнений экспертов
 Скачать 122.58 Kb. Скачать 122.58 Kb.
|
|
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько единиц изменится результативный признак при изменении факторного на 1 единицу. (Например, коэффициент b = 8.16 показывает среднее изменение результативного показателя (в единицах измерения Y) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 8.16). Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере (b = 8.16) связь прямая. 2 Для оценки степени тесноты связи вычисляются следующие коэффициенты: а) коэффициент корреляции: 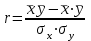 = ___________________________ = ___________________________где средние квадратические отклонения: 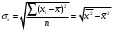 = _______________________ = _______________________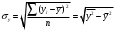 = ________________________ = ________________________Коэффициент корреляции показывает тесноту линейной связи между результативным (у) и факторным (х) признаками. Коэффициент корреляции может принимать значения 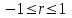 . Если . Если 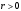 , то связь между признаками прямая, если , то связь между признаками прямая, если 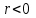 - связь обратная. - связь обратная.Для оценки тесноты связи используют шкалу: до  0,3 – связь отсутствует или очень слабая; 0,3 – связь отсутствует или очень слабая;от  0,3 до 0,3 до  0,5 – связь слабая; 0,5 – связь слабая;от  0,5 до 0,5 до  0,7 – связь умеренная; 0,7 – связь умеренная;от  0,7 до 0,7 до  1,0 – связь сильная. 1,0 – связь сильная.Вывод: __________________________________________________ б) коэффициент детерминации: D = 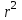 = _______________ = _______________Значение коэффициента детерминации изменяется от 0 до 1 и показывает, на сколько процентов вариация результативного признака определяется вариацией фактора, включенного в уравнение. (Например, D=0,37 значит, вариация результата Y - потребление молока и молочных продуктов на 37 % определяется вариацией фактора, включенного в уравнение, т.е. среднедушевых денежных доходов населения) Чем ближе значение коэффициента детерминации к 1, тем функция является более адекватной по данному показателю. Вывод:______________________________________________ 3) Для оценки значимости уравнения регрессии рассчитывается F – критерий Фишера: 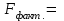 = = 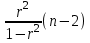 =_____________________ =_____________________Для оценки значимости уравнения регрессии 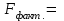 . сравнивается с Fтабл. при . сравнивается с Fтабл. при 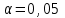 , , 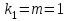 , , 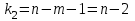 Fтабл = 6,61 Если Fфакт. > Fтабл.. уравнение регрессии значимо, статистически надежно и может быть использовано для прогнозирования. Вывод:_________________________________________ Задача 3. Прогнозирование по методу экстраполяции Вариант – такой же, как в задаче 2 Задание. Используя метод экстраполяции и предполагая линейную зависимость потребления электроэнергии по субъектам Российской Федерации от времени: построить уравнение линейного тренда и получить прогноз на 2 года вперед (2020, 2021 гг.). Отразить фактические и расчетные значения показателей потребления (включая прогноз) на графике. Исходные данные представлены в таблице 5. Потребление электроэнергии по субъектам Российской Федерации, (млн.кВт.час) ВЫБРАТЬ ДАННЫЕ ТОЛЬКО СВОЕГО ВАРИАНТА И ПРЕДСТАВИТЬ В ТАБЛИЦЕ !!!
|
