|
|
Текстовые задачи. ЕГЭ В14 выпускнику. 1) задачи на движение по прямой (навстречу и вдогонку)
Задачи В14
В задачах на движение допускается определенная идеализация: считается, что тела движутся прямолинейно и равномерно, скорости (в том числе скорость течения) постоянны в течение определенных промежутков времени, не меняются при поворотах и т.д., движущиеся тела считаются материальными точками (если не оговорено противное), т.е. не имеющими размеров и массы (вернее, их размеры и масса несущественны для решения задачи). Даже решение задач на движение по окружности не требует применения специальных понятий — угловой скорости и т.п.; здесь точнее было бы говорить о движении по замкнутой трассе. Если расстояние между пунктами, из которых начинают движение два тела, не задано, иногда бывает удобно положить его равным единице.
При решении задач на движение двух тел часто очень удобно считать одно тело неподвижным, а другое — приближающимся к нему со скоростью, равной сумме скоростей этих тел (при движении навстречу) или разности скоростей (при движении вдогонку). Такая модель помогает разобраться с условием задачи, получить нужные уравнения даже в таком относительно трудном случае, как движение по окружности.
Основными типами задач на движение являются следующие:
1) задачи на движение по прямой (навстречу и вдогонку),
2) задачи на движение по замкнутой трассе,
3) задачи на движение по воде,
4) задачи на среднюю скорость,
5) задачи на движение протяженных тел.
В задачах на движение по воде скорость течения считается неизменной. При движении по течению скорость течения прибавляется к скорости плывущего тела, при движении против
течения — вычитается из скорости тела. Скорость плота считается равной скорости течения.
В задачах на движение протяженных тел требуется, как правило, определить длину одного из них. Наиболее типичная ситуация: определение длины поезда, проезжающего мимо
столба или протяженной платформы. В первом случае поезд проходит мимо столба расстояние, равное длине поезда, во втором случае — расстояние, равное сумме длин поезда
и платформы.
В определенном смысле задачи на работу схожи с задачами на движение: роль скорости здесь играет производительность, роль расстояния — объем работы. В тех случаях, когда
объем работы в явном виде не задан, его иногда удобно принять равным единице. Существенно разных задач здесь практически нет, во всех случаях речь идет о выполнении определенной работы, меняются только сюжеты, а «математическая » фабула остается одной и той же. Иногда в задачах на работу выделяют группу задач на трубы и бассейны, решение которых, вообще говоря, не имеет никаких специфических черт по сравнению с другими задачами на работу. Иногда в задачах на совместную работу можно обойтись
без решения уравнений, используя только арифметический способ.
Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч
Пусть х км/ч - скорость лодки в неподвижной воде (собственная скорость)
|
V км/ч
|
t,ч
|
S,км
|
По течению
|
х+3
|
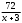
|
72
|
Против течения
|
х-3
|
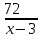
|
72
|
Моторная лодка затратила на обратный путь на 6 часов меньше, чем на путь против течения
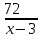 - -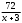 =6 (х-3)(х+3) =6 (х-3)(х+3) 0 0
72(х+3)-72(х-3)=6(х2 -9)
72(х+3-х+3)=6(х2 -9) делим на 6
х2 -9=72
х2 =81
х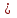 0, х=9 0, х=9
9 км/ч собственная скорость
Ответ: 9
|
Лодка в 5:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа, лодка отправилась назад и вернулась в пункт А в 23:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость лодки равна 4 км/ч
х км/час скорость течения реки
|
V км/ч
|
t,ч
|
S,км
|
По теч
|
4+x
|
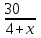
|
30
|
|
Против теч
|
4-x
|
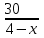
|
30
|
|
С 5:00 до 23:00 18часов
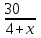 +2+ +2+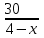 =18 =18
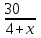 + +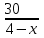 =16 =16
30(4-x)+30(4+x)=16(16-х2) , 16-х2- 0 0
240=16(16-х2)
делим на 16
15=16-х2
х2=1
х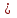 0,х=1 0,х=1
1 км/час скорость течения реки Ответ: 1
|
Теплоход проходит по течению реки до пункта назначения 209 км, и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 3 часа, а в пункт отправления теплоход возвращается через 33 часа после отплытия из него. Ответ дайте в км/ч
Пусть х км/ч- скорость течения
|
V км/ч
|
t,ч
|
S,км
|
По теч
|
15+х
|
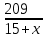
|
209
|
|
Против теч
|
15-х
|
|
209
|
|
По условию стоянка длится 3 часа, а в пункт отправления теплоход возвращается через 33 часа после отплытия из него.
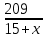 +3+ +3+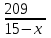 =33 =33
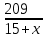 + +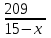 =30 =30
209(15-х)+209(15+х)=30(225-х2), 225-х2 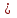 0 0
6270=6750-30х2
209=225- х2
х2 =16
х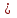 0 , х=4 0 , х=4
4 км/ч- скорость течения Ответ: 4
|
|
|
|
Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Пусть скорость велосипедиста x, скорость мотоциклиста y/
|
скорость
|
время
|
расстояние
|
велосипедист
|
x
|
40мин=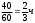
|
 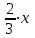
|
мотоцилист
|
y
|
10мин=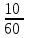 = =
=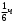
|
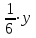 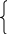
|
Мотоциклист догнал велосипедиста в первый раз (Оба проехали одинаковые расстояния)
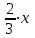 = =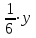
y=4x
|
|
Скорость
|
время
|
расстояние
|
Велосип.
|
х
|
30мин=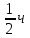
|
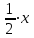
|
Мотоцикл.
|
y
|
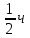
|
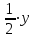
|
Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна 30 км. Получим второе уравнение:
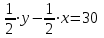
y-x=60
y=4x
y-x=60 4x-x=60
3x=60
x=20 y=80
20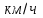 - скорость велосипедиста - скорость велосипедиста
80 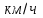 скорость мотоциклиста скорость мотоциклиста
Ответ: 80
|
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам
1,5 км/ч=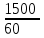 м/мин=25м/мин м/мин=25м/мин
|
Скорость, м/мин
|
Время,мин
|
Расстояние,м
|
1пешеход
|
х+25
|
у
|
(х+25)у
|
2пешеход
|
х
|
у
|
ху
|
расстояние между пешеходами равно 300 метров
(х+25)у- ху=300
ху+25у-ху=300
25у=300
у=12
Через 12 мин Ответ: 12
Из городов A и B, расстояние между которыми равно 390 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 210 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч
390-210=180 (км)-путь от А до встречи
180: 3=60( км/ч) скорость автомобиля, выехавшего из города A.
Ответ: 60
|
Из одной точки круговой трассы, длина которой равна 27 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 113 км/ч, и через 45 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч
Пусть х км/ч- скорость второго автомобиля.
|
v,км/ч
|
t,ч
|
s,км
|
1в
|
113
|
45мин==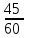 ч= ч=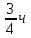
|
113∙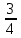
|
2 в
|
х
|
45мин=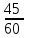 ч= ч=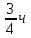
|
х∙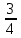
|
Первый автомобиль после старта опережал второй автомобиль
на один круг. Это и есть секрет данной задачи. Один круг — это длина
трассы, она равна 27 км
113∙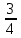 - х∙ - х∙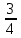 =27 умножим на 4 =27 умножим на 4
339-3х=108
3х=339-108
3х=231
х=77 км/ч- скорость второго автомобиля. Ответ: 77
|
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 1 минуту после отправления он догнал велосипедиста в первый раз, а еще через 21 минуту после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 35 км. Ответ дайте в км/ч
|
скорость
|
время
|
расстояние
|
велосипедист
|
x
|
11 мин=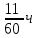
|
 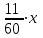
|
мотоцилист
|
y
|
1 мин=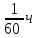
|
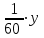
|
Мотоциклист догнал велосипедиста в первый раз(Оба проехали одинаковые расстояния)
 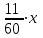 = =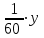 умножим на 60 умножим на 60
11х=y
|
|
Скорость
|
время
|
расстояние
|
Велосип.
|
х
|
21мин=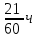
|
х∙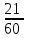
|
Мотоцикл.
|
y
|
21мин=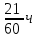
|
y∙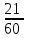
|
Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна 35 км. Получим второе уравнение:
y∙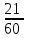 - х∙ - х∙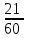 =35 умножим на 60 =35 умножим на 60
21y-21x=2100 делим на 21
y-x=100

11х=y
y-x=100
11x-x=100
10x=100
x=10 y=100+10=110
110 км/ч - скорость мотоциклиста
Ответ: 110
|
Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах 30 мин=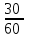 ч= ч=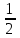 ч ч
Пусть х км/ч – скорость автомобиля ,y км – расстояние от А до С
1) от города А до города С
|
Скорость, км/ч
|
Время,ч
|
Расстояние,км
|
Мотоциклист
|
90
|
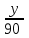
|
y
|
Автомобиль
|
х
|
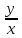
|
y
|
По условию задачи известно, что из города A в город B выехал автомобиль, а через 30 минут следом за ним выехал мотоциклист,
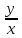 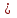 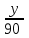 на на 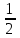
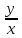 - -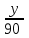 = =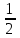
2)С момента встречи в городе С :
|
Скорость, км/ч
|
Время,ч
|
Расстояние,км
|
Мотоциклист
|
90
|
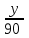
|
y
|
Автомобиль
|
х
|
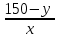
|
150-y
|
|
По условию задачи известно, автомобиль потратил время на прибытие в пункт В и мотоциклист в пунк А одинаковое
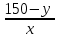 = =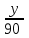
3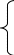 ) ) 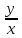 - -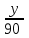 = =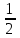 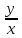 - -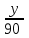 = =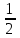
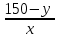 = =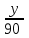 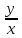 = =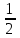 + +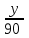
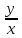 = =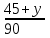
х=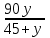
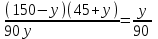
6750+150y-45y-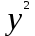 = =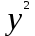
2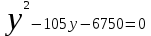
D=11025+54000=65025
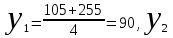 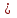 0 0
90 км – расстояние от А до С
Ответ: 90
|
Из двух городов, расстояние между которыми равно 270 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 55 км/ч и 80 км/ч
55+80=135( км/ч)- скорость сближения
270: 135=2(ч)-через столько часов автомобили встретятся
Ответ: 2
|
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 71 км/ч, а вторую половину времени — со скоростью 81 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч
Пусть x (ч)- общее время
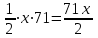 км путь на первом участке пути км путь на первом участке пути
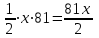 км путь на втором участке пути км путь на втором участке пути
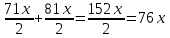 км общий путь км общий путь
76х : х=76 (км/ч) средняя скорость
Ответ: 76
|
Первые три часа автомобиль ехал со скоростью 90 км/ч, следующие три часа — со скоростью 75 км/ч, а затем один час — со скоростью 65 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч
90∙3+3∙75+1∙65=560(км)-общее расстояние
3+3+1=7(ч)-общее время
560:7=80(км/ч)- средняя скорость автомобиля на протяжении всего пути.
Ответ: 80
|
Первую половину трассы автомобиль проехал со скоростью 38 км/ч, а вторую – со скоростью 57 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Пусть половина пути х км, весь путь 2х км
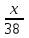 ч - время на прохождение первой половины пути ч - время на прохождение первой половины пути
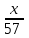 ч- время на прохождение второй половины пути ч- время на прохождение второй половины пути
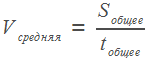
2х (км)- общее расстояние
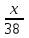 + +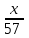 = =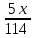 (ч)- общее время (ч)- общее время
2х: 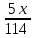 = =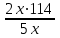 =45,6 ( =45,6 (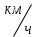 )-средняя скорость )-средняя скорость
Ответ:45,6
|
Первые 170 км автомобиль ехал со скоростью 60 км/ч, следующие 100 км — со скоростью 100 км/ч, а затем 110 км — со скоростью 120 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч
170:60=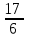 ч время первого участка ч время первого участка
100:100=1ч время второго участка
110:120=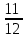 ч время третьего участка ч время третьего участка
170+100+110=380(км)-общий путь
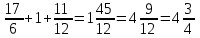 ч – общее время ч – общее время
380:4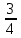 = =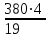 =80 (км/ч) =80 (км/ч)
Ответ:80
|
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть — со скоростью 120 км/ч, а последнюю — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч
Пусть х км –путь (общий)
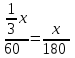 (ч)-время на первом участке пути (ч)-время на первом участке пути
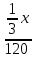 = =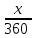 (ч)-время на втором участке пути (ч)-время на втором участке пути
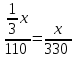 (ч)-время на третьем участке пути (ч)-время на третьем участке пути
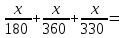 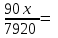 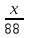 (ч)-общее время (ч)-общее время
x : 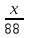 =88 (км/ч) =88 (км/ч)
Ответ: 88
|
Путешественник переплыл море на яхте (со средней) скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем только, что это расстояние было одинаковым на пути туда и обратно. Для простоты примем это расстояние за 1 . Тогда время, которое путешественник плыл на яхте, равно 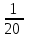 , а время, затраченное на полет, равно , а время, затраченное на полет, равно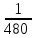 . .
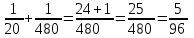 (ч)- общее время (ч)- общее время
2 – общее расстояние
Средняя скорость равна
2: 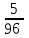 = =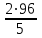 =38,4 =38,4
Ответ:38,4
|
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 300 метров, за 1 минуту 15 секунд. Найдите длину поезда в метрах
Пусть длина поезда х м
| |
|
|
 Скачать 0.7 Mb.
Скачать 0.7 Mb.
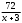
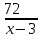
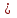 0
0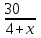
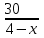
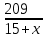
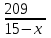 =33
=33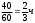

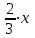
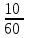 =
=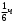
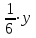
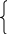
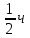
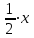
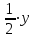
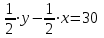
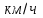 - скорость велосипедиста
- скорость велосипедиста 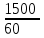 м/мин=25м/мин
м/мин=25м/мин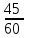 ч=
ч=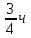
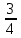
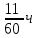
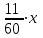
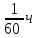
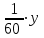
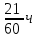
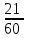

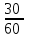 ч=
ч=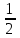 ч
ч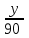
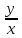
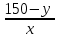
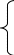 )
) 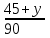
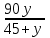
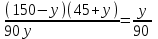
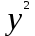 =
=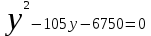
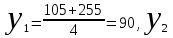
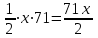 км путь на первом участке пути
км путь на первом участке пути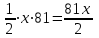 км путь на втором участке пути
км путь на втором участке пути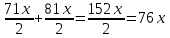 км общий путь
км общий путь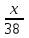 ч - время на прохождение первой половины пути
ч - время на прохождение первой половины пути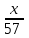 ч- время на прохождение второй половины пути
ч- время на прохождение второй половины пути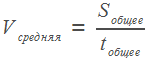
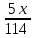 (ч)- общее время
(ч)- общее время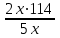 =45,6 (
=45,6 (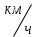 )-средняя скорость
)-средняя скорость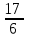 ч время первого участка
ч время первого участка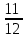 ч
ч 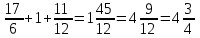 ч – общее время
ч – общее время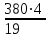 =80 (км/ч)
=80 (км/ч)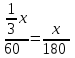 (ч)-время на первом участке пути
(ч)-время на первом участке пути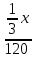 =
=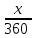 (ч)-время на втором участке пути
(ч)-время на втором участке пути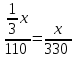 (ч)-время на третьем участке пути
(ч)-время на третьем участке пути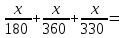
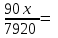
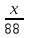 (ч)-общее время
(ч)-общее время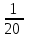 , а время, затраченное на полет, равно
, а время, затраченное на полет, равно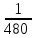 .
. 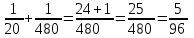 (ч)- общее время
(ч)- общее время 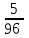 =
=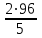 =38,4
=38,4