вышая матиматика. эгзамен. 13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
23. общее уравнение линий второго порядкаУравнения кривых второго порядка с осями симметрии, параллельными координатным ос 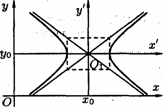 ям ямНайдем сначала уравнение эллипса с центром в точке 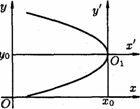 стемы координат стемы координатВэ 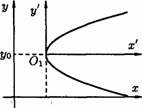 той системе координат уравнение Рис.41. той системе координат уравнение Рис.41.эллипса имеет вид Та 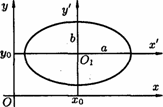 к как к какуравнение эллипса запишется в виде Аналогично рассуждая, получим уравнение гиперболы с центром в точке И, наконец, параболы, изображенные на рисунке 43, имеют соответствующие уравнения. 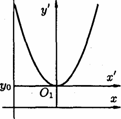 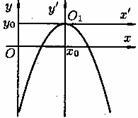 Уравнение Ac2 + Су2 + 2Dx + 2Еу + F = О Уравнения эллипса, гиперболы, параболы и уравнение окружности где коэффициенты А и С не равны нулю одновременно. Возникает вопрос: всякое ли уравнение вида (11.14) определяет одну из кривых (окружность, эллипс, гипербола, парабола) второго порядка? Ответ дает следующая теорема. Теорема 11.2. Уравнение (11.14) всегда определяет: либо окружность (при А=С), либо эллипс (при А • С > 0), либо гиперболу (при А • С < 0), либо параболу (при АС = 0). При этом возможны случаи вырождения: для эллипса (окружности) - в точку или мнимый эллипс (окружность), для гиперболы - в пару пересекающихся прямых, для параболы - в пару параллельных прямых Пример 11.1. Установить вид кривой второго порядка, заданной уравнением Решение: Предложенное уравнение определяет эллипс 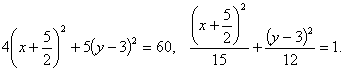 Получилось каноническое уравнение эллипса с центром в Получилось каноническое уравнение параболы с вершиной в точке Пример 11.3. Установить вид кривой второго порядка, заданной уравнением Решение: Преобразуем уравнение: 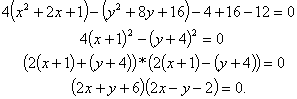 Это уравнение определяет две пересекающиеся прямые Общее уравнение второго порядка Рассмотрим теперь общее уравнение второй степени с двумя неизвестными: Ax2 + 2Вху + Су2 + 2Dx + 2Еу + F == 0. (11.15) Оно отличается от уравнения (11.14) наличием члена с произведением координат Используя формулы поворота осей выразим старые координаты через новые: 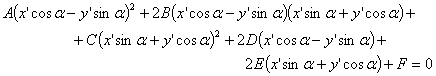 Выберем угол Выберем уголт.е. т.е. Отсюда |
