вышая матиматика. эгзамен. 13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
Это – формула деления отрезка в данном отношении λ. В частности, при λ = 1 (т.е. разделить отрезок пополам), т.е когдаАМ =МВ, имеемx = x1 +2 x2 ,y = y1 +2 y2 − координаты середины отрезкаАВ. Лекция № 5 Аналитическая геометрия на плоскости проф. Дымков М.П. 50 Замечание. Еслиλ = 0, то точкиА иМ совпадают. Еслиλ < 0, то точкаМ лежитвне отрезкаАВ – говорят, что точкаМ делит отрезоквнешним образом (λ ≠ −1, т.к. тогда бы выполнялосьAMMB = −1 илиAM + MB = 0, т.е.AB = 0, что невозможно, если точки различны). 2. Площадь треугольника АВС с вершинами A(x1, y1 ), B(x2 , y2 ), C(x3, y3).
Если из данной формулы получилось отрицательное число, то следует взять по его абсолютной величине. Если же S∆ = 0 точки лежат на одной прямой (не существует треугольник). 2. Гиперболой называется множество всех точек плоскости,модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемыхфокусами, есть величина постоянная,меньшая, чем расстояние между фокусами. Если ввести обозначения, аналогичные предыдущему, то аналитически описанное геометрически свойство означает, что
3. Параболой называется множество всех точек плоскости, каждая из которыходинаково удалена отданной точки, называемойфокусом, и данной прямой, называемойдиректрисой.Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p( p> 0) . Для вывода уравнения выберем систему координат Oху так, чтобыось Oх проходила через фокусF перпендикулярно директрисе в направленииот директрисы кF, а начало координат расположим посередине между фокусом и директрисой.
17.Линии на плоскости Определение. Линия на плоскости – множество точек плоскости, обладающих некоторым только им присущим геом етрическим свойством. Определение. Уравнением линии на плоскости называется такое уравнение с двумя переменными, которому удовлетворяют координаты каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Определение. Уравнением линии в полярной системе координат называется уравнение , если координаты любой точки, лежащей на этой линии, и только они, удовлетворяют этому уравнению. Линию на плоскости можно задать параметрическими уравнениями где и – непрерывны по параметру . Чтобы перейти от параметрических уравнений к уравнению вида надо из двух уравнений исключить параметр . Линию на плоскости можно задать векторным уравнением , где – скалярный переменный параметр. Этому уравнению в системе координат соответствуют два скалярных уравнения . Векторное уравнение и параметрические уравнения линии имеют механический смысл: при перемещении точки на плоскости указанные уравнения называются уравнениями движения, а линия – траекторией точки, параметр при этом есть время. 18. уравнение прямой линии на плоскости Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxyи в ней задана прямая линия. Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости. Другими словами, уравнение прямой на плоскости в прямоугольной системе координат Oxy есть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой. Осталось разобраться с вопросом, какой вид имеет уравнение прямой на плоскости. Ответ на него содержится в следующем пункте статьи. Забегая вперед, отметим, что существуют различные формы записи уравнения прямой, что объясняется спецификой решаемых задач и способом задания прямой линии на плоскости. Итак, приступим к обзору основных видов уравнения прямой линии на плоскости. Уравнение Поясним смысл теоремы. Заданному уравнению вида Посмотрите на чертеж.  С одной стороны можно сказать, что эта линия определяется общим уравнением прямой вида Общее уравнение прямой называется полным, если все числа А, В и С отличны от нуля, в противном случае общее уравнение прямой называется неполным. Неполное уравнение прямой вида Таким образом, любую прямую на плоскости в заданной прямоугольной системе координат Oxy можно описать с помощью общего уравнения прямой при некотором наборе значений чисел А, В и С. Нормальный вектор прямой, заданной общим уравнением прямой вида Все уравнения прямых, которые приведены в следующих пунктах этой статьи, могут быть получены из общего уравнения прямой, а также могут быть обратно приведены к общему уравнению прямой. Рекомендуем к дальнейшему изучению статью общее уравнение прямой. Там доказана теорема, сформулированная в начале этого пункта статьи, приведены графические иллюстрации, подробно разобраны решения примеров на составление общего уравнения прямой, показан переход от общего уравнения прямой к уравнениям другого вида и обратно, а также рассмотрены другие характерные задачи. 19.уравнение прямой на плоскости Каноническое уравнение прямой на плоскости в прямоугольной декартовой системе координат Oxy имеет вид  , где , где Очевидно, что прямая линия, определяемая каноническим уравнением прямой, проходит через точку  в прямоугольной системе координат Oxy на плоскости соответствует прямой, проходящей через точку в прямоугольной системе координат Oxy на плоскости соответствует прямой, проходящей через точку Для примера изобразим на плоскости прямую линию, соответствующую каноническому уравнению прямой вида  . Очевидно, что точка . Очевидно, что точка  Каноническое уравнение прямой вида  используют даже тогда, когда одно из чисел или равно нулю. В этом случае запись используют даже тогда, когда одно из чисел или равно нулю. В этом случае запись  считают условной (так как содержится ноль в знаменателе) и ее следует понимать как считают условной (так как содержится ноль в знаменателе) и ее следует понимать как 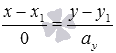 и определяет прямую, параллельную оси ординат (или совпадающую с ней). Если , то каноническое уравнение прямой принимает вид и определяет прямую, параллельную оси ординат (или совпадающую с ней). Если , то каноническое уравнение прямой принимает вид 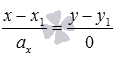 и определяет прямую, параллельную и определяет прямую, параллельную | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

