вышая матиматика. эгзамен. 13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
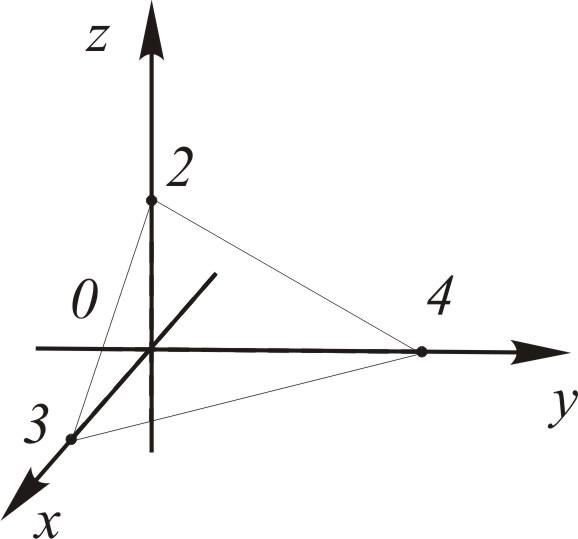
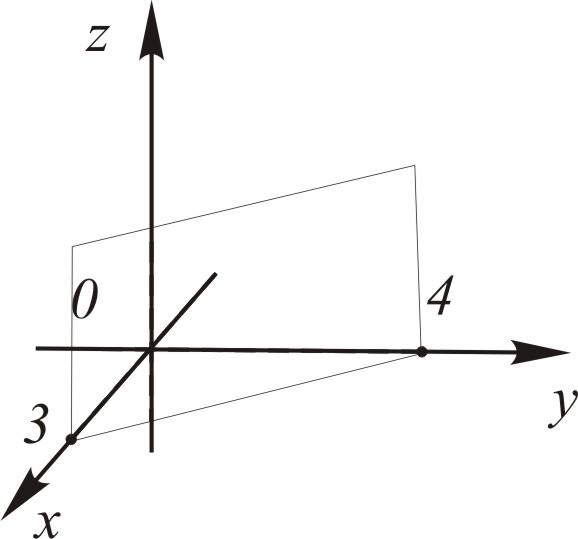
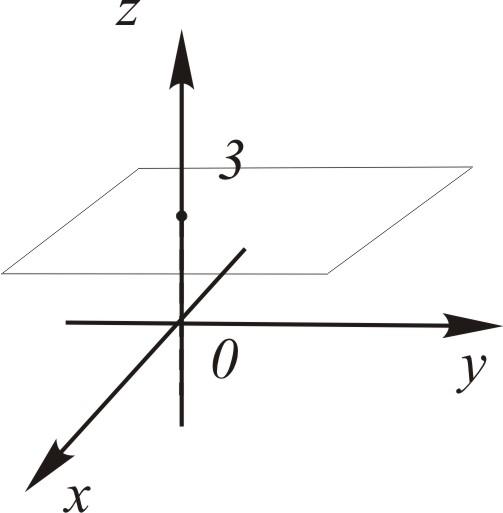
24. Уравнение поверхности и линии в пространствеПусть задана ДСК в пространстве. Уравнением поверхности называется такое уравнение Линию в пространстве можно рассматривать как линию пересечения поверхностей: 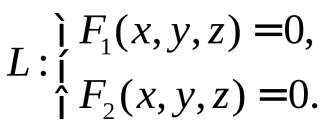 Плоскость описывается общим уравнением вида где хотя бы один из коэффициентов 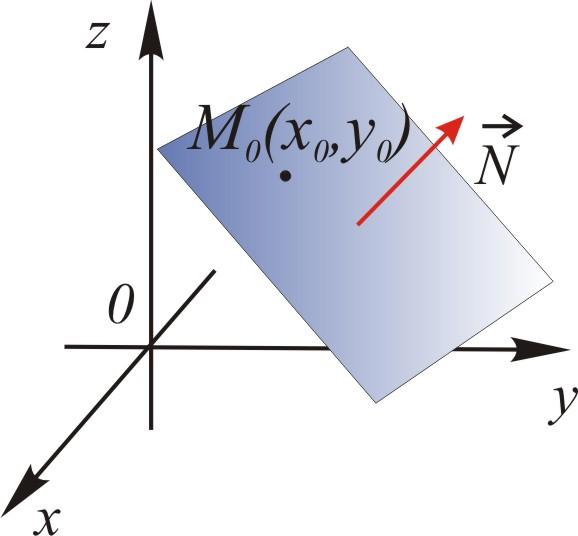 . 4. Дано: точка . 4. Дано: точка Найти: уравнение плоскости, проходящей через точку Решение. Выберем на плоскости произвольно точку – уравнение плоскости по точке и нормали (любой ненулевой вектор, перпендикулярный плоскости, будем называть нормалью). Приведем без доказательства еще два вида уравнений плоскости. Ур 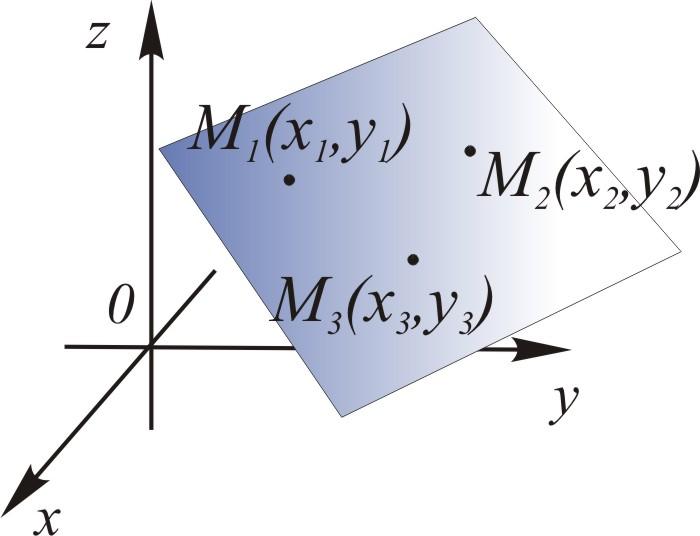 авнение плоскости, проходящей через точки авнение плоскости, проходящей через точки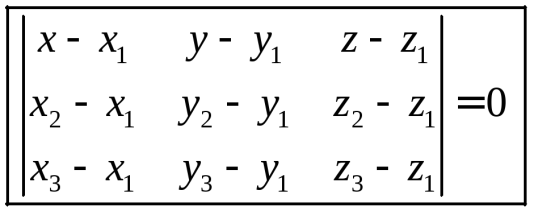 . .Уравнение плоскости, отсекающей на осях координат ненулевые «отрезки» 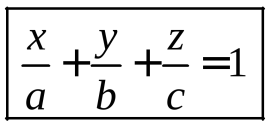 . .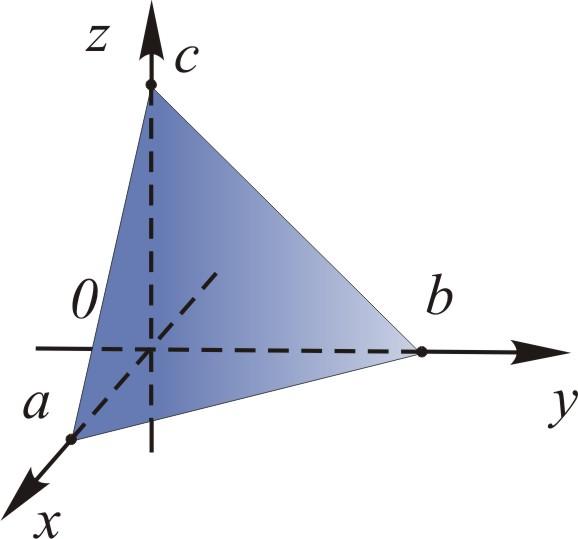 Замечания. - Если в уравнении плоскости свободный член - Если в уравнении отсутствует какая-либо координата, то плоскость проходит параллельно соответствующей оси. - Коэффициенты при - Уравнения координатных плоскостей
Прямая в пространстве задается каноническим, параметрическим или общим уравнениями. 1. 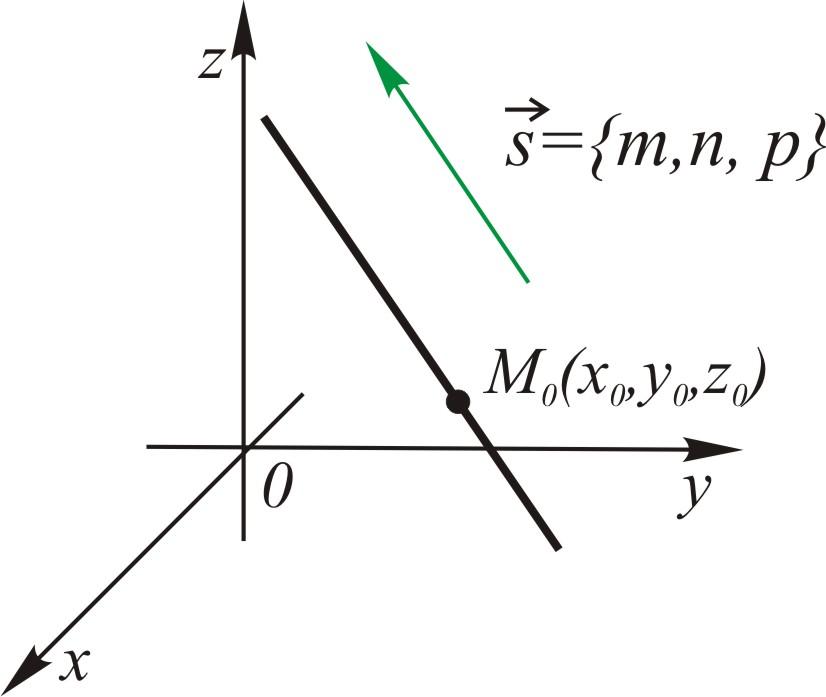 Найдем уравнение прямой, проходящей через заданную точку Найдем уравнение прямой, проходящей через заданную точку Выберем на прямой произвольно точку 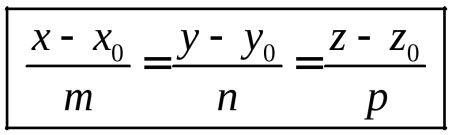 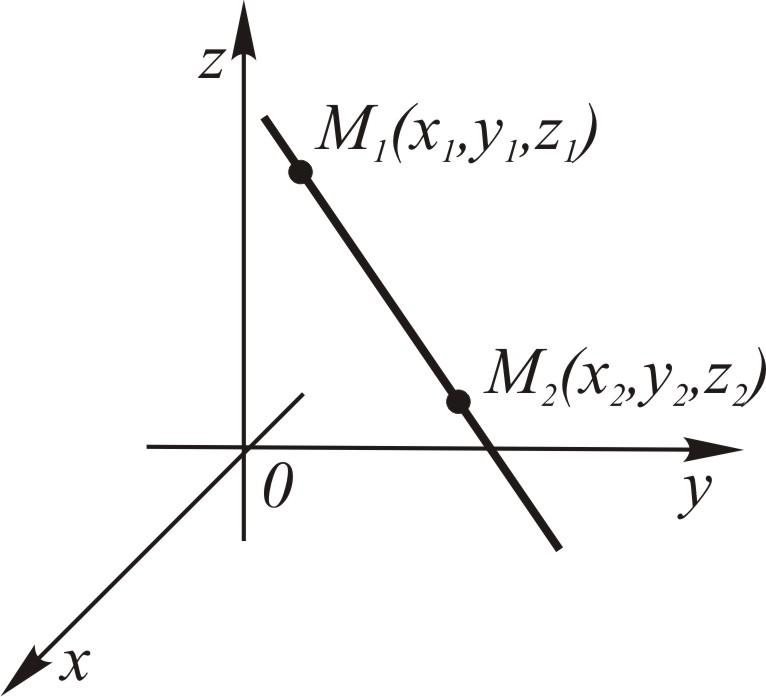 . .Это уравнение называется каноническим уравнением прямой в пространстве. 1а. Рассуждая аналогично, получим уравнение прямой по двум ее точкам 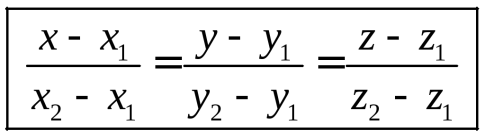 . .2. Введем в каноническом уравнении параметр 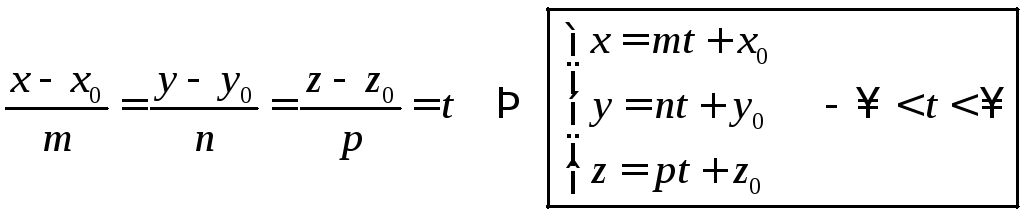 . .Уравнение прямой в таком виде называется параметрическим. При фиксированном значении параметра получаем соответствующую точку прямой. Придавая 3. 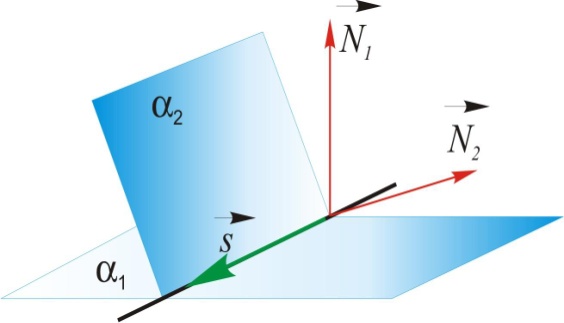 Также прямую можно задать как линию пересечения непараллельных плоскостей. Также прямую можно задать как линию пересечения непараллельных плоскостей.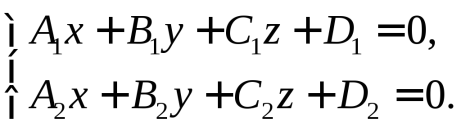 Такое уравнение называется общим. Почему «альфа»??? Для решения задач, необходимо уметь переходить от одной формы записи прямой к другой. 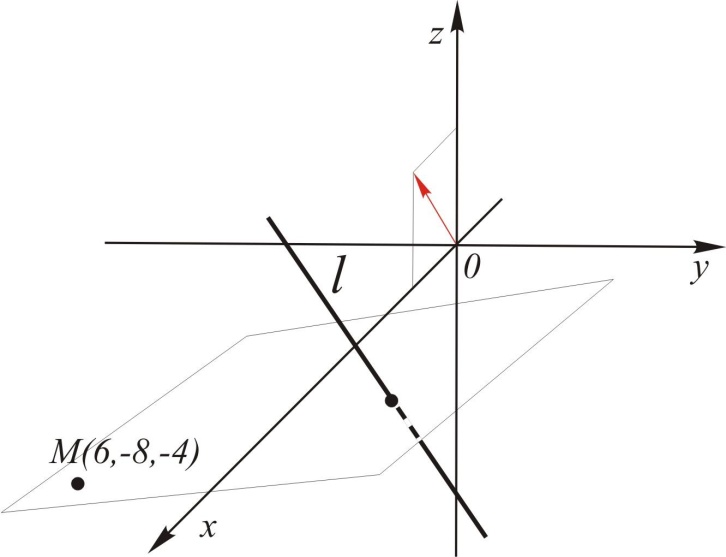 айти расстояние от точки айти расстояние от точки Решение. Убедимся, что |