вышая матиматика. эгзамен. 13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения

• Название: 13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения
• Анкор: вышая матиматика
• Дата: 04.10.2022
• Размер: 0.81 Mb.
• Имя файла: эгзамен.docx
• Тип: Документы; #712870
• страница: 2 из 7

15.Выражение смешанного произведения через координаты векторов.

а=а_хi+a_yj+a_zk, b= b_хi+b_yj+b_zk, c= c_хi+c_yj+c_zk

abc=(a×b)c= (c_xi+c_yj+c_zk)=

=( i- j+ k) (c_xi+c_yj+c_zk) = c_x- c_y+ c_z

abc=

Т.о. объем параллелепипеда: V=±

V 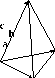_пир.= S_{осн. пир.} Н=  S_{осн. парал.}Н=±

Следствие. Критерий компланарности: три вектора a,b и c компланарны тогда и только тогда, когда abc= =0 (в частности, любые два из них коллениарны).

Приложение смешанного произведения.

1. 
   Определение ориентации тройки векторов. Если abc>0, то тройка векторов, которая его образует, является правой.
   

Если abc<0, то тройка векторов, которая его образует, является левой.

2. 
   Определение компланарности векторов.
   
3. 
   Вычисление объемов параллелепипеда и тетраэдра, построенного на векторах.
   

Пример. Определить ориентацию тройки векторов ijk.

ijk= =1>0 – правая тройка векторов.

Двойное векторное произведение.

Пусть даны три произвольных вектора a, b и c. Если вектор b векторно умножается на вектор с, а вектор а также векторно умножается на векторное произведение bc, то полученный при этом вектор а(bc)=[a[bc]] называется двойным векторным произведением.

Теорема. (Док-во на с.79). Для любых векторов a, b и c справедлива формула:

а(bc)=[a[bc]]=b(ac)-c(ab) (13)

Из формулы (13)  (аb)c=[[ab]c]=b(ac)-a(bc) (13)

(Т.е. средний вектор, умноженный на скалярное произведение двух остальных, минус другой вектор внутреннего произведения, умноженный на скалярное произведение двух остальных.)

16.система координат на плоскости

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки на плоскости.

Одной из таких систем является прямоугольная (декартова) система координат.

Прямоугольная система задается двумя взаимно-перпендикулярнымипрямыми –осями, на каждой из которых: 1) выбрано положительное направление и 2) задан (единичный) (масштабный) отрезок.Обычно, единицу масштаба берут одинаковой для обеих осей.

1.Расстояние d между двумя точкамиA(x1, y1 ) иB(x2 , y2 ).

Искомое расстояние равно длине вектора AB (x2 − x1;y2 − y1 ). Координа-

ты вектора получаются путем вычитания координат точки А (начала вектора) из координат точкиВ – конца вектора.

.

(x2− x1)2 + (y2− y1)2

Тогда

d =

(

,

)=

AB

AB

Деление отрезка в данном отношении.

Требуется разделить отрезок АВ, соединяющий точкиA(x1,y1 ) иB(x2 ,y2 )

в заданном отношении λ > 0 , т.е. надо найти

точку М (х,у) отрезкаАВ такую,

что

AM = λ .

А

MB

у

Решение. Рассмотрим векторы

и

. Тогда

М

AM

MB

факт, что М делит отрезовАВ в отношенииλ означает,

В

что

= λ

или в координатной записи:

AM

MB

λ(x

− x)

x − x

2

0

х

1

=

λ(y

.

y − y

2

− y)

1

Отсюда, x − x = λx

2

−λx или

x =

x1+ λx2

.

Аналогично,

y =

y1+ λy2

.

1

1+λ

1+λ