вышая матиматика. эгзамен. 13. Выражение векторного произведения через координаты. Некоторые приложения векторного произведения
 Скачать 0.81 Mb.
|
20. Параметрические уравнения прямой на плоскости.Параметрические уравнения прямой на плоскости имеют вид 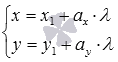 , где  и – некоторые действительные числа, причем и одновременно не равны нулю, а - параметр, принимающий любые действительные значения.Параметрические уравнения прямой устанавливают неявную зависимость между абсциссами и ординатами точек прямой линии с помощью параметра (отсюда и название этого вида уравнений прямой). Пара чисел 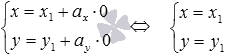 , которые вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра , представляет собой координаты некоторой точки прямой. К примеру, при имеем  , то есть, точка с координатами  лежит на прямой.Следует отметить, что коэффициенты и при параметре в параметрических уравнениях прямой являются координатами направляющего вектора этой прямой. Для примера приведем параметрические уравнения прямой вида  . Эта прямая в прямоугольной системе координат Oxy на плоскости проходит через точку с координатами и имеет направляющий вектор  .В статье параметрические уравнения прямой на плоскости Вы можете ознакомиться с подробным решением примеров и задач по этой теме. 21. Линии 2-го порядка на плоскости. Основные понятия. Рассмотрим линии, уравнения которых задаются в виде выражений, в которых переменные и входят с степенью не выше второй, т. е. имеют вид  где, по крайней мере один из коэффициентов  не равен нулю. Такие линии называютсялиниями (кривыми) второго порядка.Окружность. Окружностью с центром в точке радиуса называется множество всех точек плоскости, удаленных от точки на расстояние . Пусть центр окружности имеет координаты  , – некоторая её точка (рис. 23). Тогда по определению расстояние или . Возведя обе части равенства в квадрат, получим каноническое уравнение окружности  Если  , то центр окружности находится в начале координат и каноническое уравнение имеет вид .Эллипс. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. 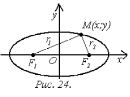 Выберем фокусы эллипса  и  , лежащие на оси  . Тогда расстояние между ними будет равно Пусть  – произвольная точка эллипса и  (рис. 24). Тогда т. е. Перенесем второй корень вправо  Возведем обе части в квадрат и раскроем скобки  Приведя подобные, сократив обе части на 4, получим  или  Обозначив  получим  или Это и есть каноническое уравнение эллипса. Если , то эллипс превращается в окружность 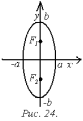 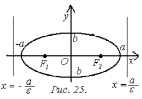. Числа и называютсябольшой и малой осями эллипса. Величина  называется эксцентриситетом эллипса. Заметим, что у эллипса всегда . Если ,(случай окружности) то , следовательно и . Если , то фокусы эллипса расположены на оси (рис. 24). Прямые называются директрисами эллипса (рис. 25).  |