гидравлика. !!ЛЕКЦ ЛАД ГИДР,2020. 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика

• Название: 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика
• Анкор: гидравлика
• Дата: 02.04.2021
• Размер: 1.61 Mb.
• Имя файла: !!ЛЕКЦ ЛАД ГИДР,2020.doc
• Тип: Документы; #190578
• страница: 4 из 9

4.5.3. Уравнение Бернулли

для элементарной струйки реальной жидкости

Реальная жидкость считается несжимаемой, обладающей важным физическим свойством - вязкостью, поэтому для реальной жидкости часто применяют словосочетание «реальная, вязкая жидкость».

Вязкость противодействует относительному перемещению слоёв жидкости, в связи с чем возникают силы трения. На преодоление сил трения затрачивается энергия (напор) движущейся жидкости. Это значит, что полный напор Н или полная удельная энергия Е струйки не остаются постоянными по длине движущейся струйки, часть напора (энергии) затрачивается на преодоление сил трения.

В уравнение Бернулли вводится дополнительный член , называемый потерями напора. Таким образом, если Н₁ – полный напор в первом сечении струйки, то ко второму сечению останется полный напор Н₂, а часть напора израсходуется на преодоление гидравлических сопротивлений между первым и вторым сечениями: (4.11)

Уравнение Бернулли для элементарной струйки реальной жидкости принимает вид: (4.12)

Представим вторую диаграмму уравнения Бернулли для элементарной струйки реальной жидкости на рис. 4.5.

Чтобы проследить подобие построения диаграммы (см. рис. 4.4) выделим два сечения 1-1 и 2-2 с площадями живых сечений dω₁ и dω₂. Покажем напоры в первом живом сечении: геометрический z₁, пьезометрический 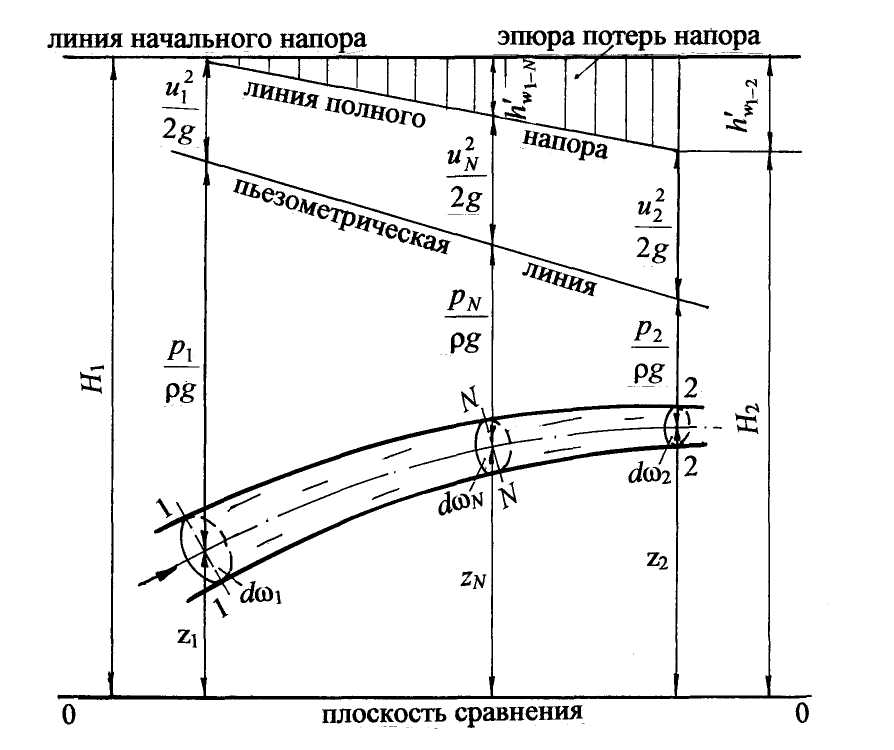, скоростной и полный напор Н₁.


Рис. 4.5

Представим на диаграмме линию начального напора – это горизон-тальная линия, проведённая от значения полного напора в первом сечении.

Полный напор во втором сечении Н₂ меньше полного напора в первом сечении Н₁ на величину потерь напора в гидравлических сопротивлениях между первым и вторым сечениями - (см. формулы (4.11), (4.12)). Покажем на диаграмме Н₂ и .

Для второго сечения аналогично отложим три напора: геометрический z₂,

пьезометрический ,

скоростной , причём > , так как dω₁> dω₂. При повышении скоростного напора сумма ( ) уменьшается, пьезометрическая линия понижается.

Проведём линию полного напора и пьезометрическую линию. Изменение линии полного напора и пьезометрической линии по длине струйки и потока жидкости правильной геометрической формы (цилиндрической, конической, плавно изменяющейся и им подобных) подчиняется линейному закону.

Если выбрать любое сечение N – N по длине движущейся струйки, то для него можно показать потери напора между сечением 1 и сечением N ( ) в виде вертикальной линии между линией начального напора и линией полного напора (см. рис. 4.5).

Таким образом, вертикальные штриховые линии между линией начального напора и линией полного напора будут соответствовать потерям напора по длине реальной струйки, а заштрихованная часть называться эпюрой потерь напора (см. рис 4.5).
4.5.4. Уравнение Бернулли

для целого потока реальной жидкости
Переходя к целому потоку, учитываем струйную модель потока, значит, чтобы записать уравнение для целого потока нужно просуммировать энергии составляющих поток струек по всему живому сечению потока.

Рассмотрим теоретические положения по уравнению Бернулли для потока реальной жидкости.

Два слагаемых уравнения соответствуют статическому напору Н_ст согласно формуле (4.9). В гидродинамике принято считать: распределение статического напора по живому сечению подчиняется гидростатическому закону: (4.13)

Покажем этот закон графически на рис. 4.6.

В заданном живом сечении потока ω выделим произвольно элементарные струйки 1, 2, 3, давления в которых р₁, р₂, р₃ соответственно. Проведём плоскость сравнения 0-0 и покажем геометрические высоты , , живых сечений струек.

На уровне выбранных струек покажем пьезометры и соответственно пьезометрические напоры: .

Уровни жидкости во всех пьезометрах будут на одном горизонте, а сумма

Определённая постоянная величина статического напора будет в данном живом сечении, в другом живом сечении она будет также постоянной, но другой величины.

Следующая задача – просуммировать кинетические энергии струек, составляющих поток, по живому сечению потока. Скорости струек (u) в пределах живого сечения потока переменны, поэтому следует учесть неравномерность распределения скорости по живому сечению.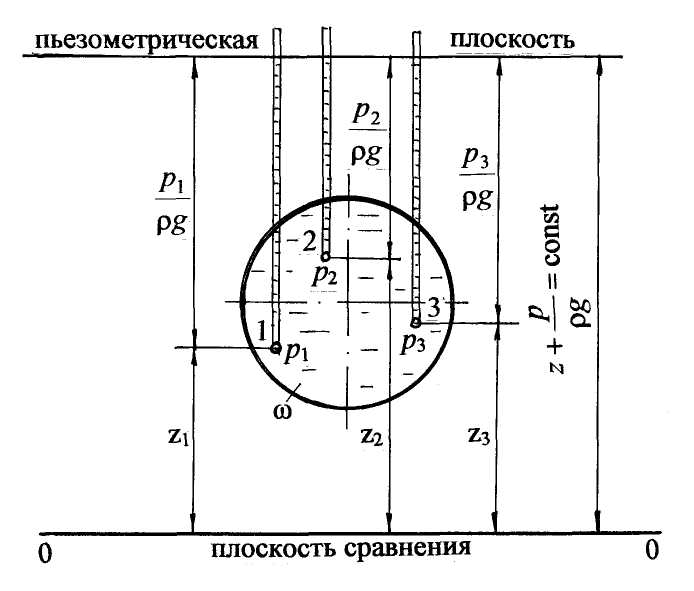

Рис. 4.6

Для практических расчётов вводят среднюю или условную скорость потока υ (раздел 4.4), одинаковую для всех струек. Теоретически рассчитывают условную кинетическую энергию через среднюю скорость потока υ.

Затем теоретически определяют действительную кинетическую энергию через действительные скорости u элементарных струек, составляющих поток.

Неравномерность распределения скорости по живому сечению учитывают коэффициентом корреляции кинетической энергии, или коэффициентом неравномерности распределения скорости – α:

Коэффициент α называется также коэффициентом Кориолиса.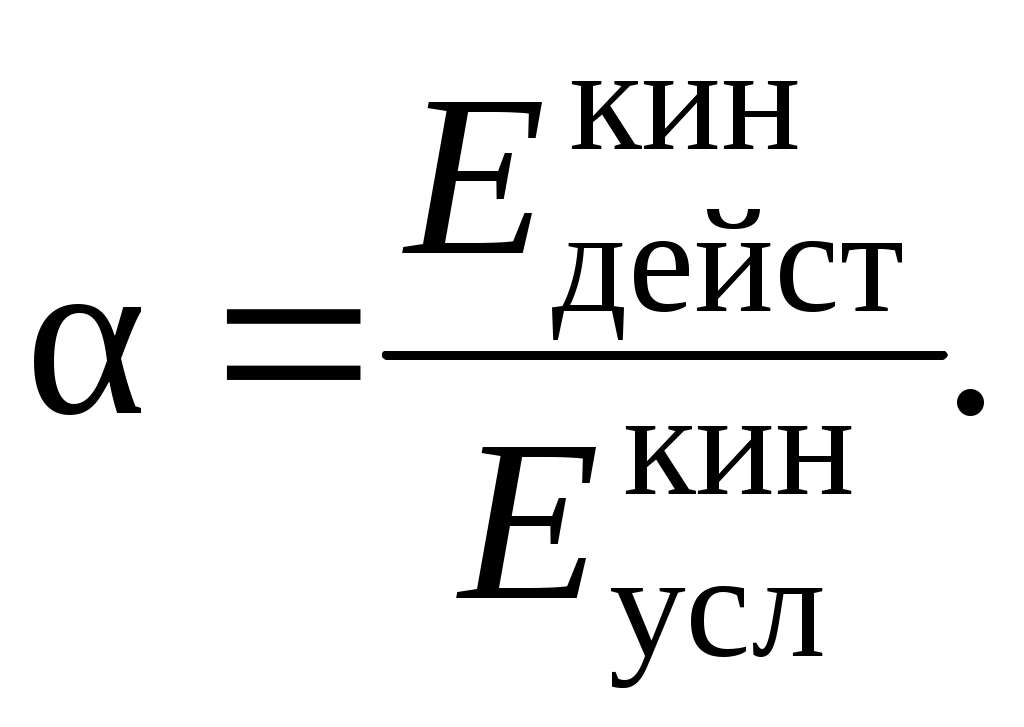

(4.14)

Значение коэффициента α зависит от режима движения жидкости. Режимы движения жидкости будут рассмотрены ниже.

Пока следует учесть, что для ламинарного режима α = 2,0; для турбулентного режима α = 1,0 1,15 (для практических расчётов при турбулентном режиме воды принимают α = 1,0).

С учётом введённого коэффициента α скоростной напор h_ск или удельная кинетическая энергия потока e_кин представляется как .

Дополнительный член уравнения Бернулли для элементарной струйки реальной жидкости учитывает потери напора в элементарной струйке.

Для целого потока вводится осреднённая величина потерь напора h_w. Аналогично средней скорости считается, что суммарные потери напора элементарных струек с действительными величинами условно равны полным потерям напора для потока h_w.

С учётом вышеизложенных положений уравнение Бернулли для целого потока реальной жидкости принимает вид:

(4.15)

Уравнение (4.15) является основным уравнением гидродинамики, которым пользуются для решения теоретических и инженерных задач.

Диаграмма уравнения для целого потока реальной жидкости аналогична диаграмме для элементарной струйки реальной жидкости (см. рис. 4.5). На диаграмме следует обозначить живые сечения ω₁ и ω₂, а скоростные напоры - соответственно

Рассмотрим практическое применение уравнения Бернулли.
4.5.5. Экспериментальное определение статического и полного

напоров. Расчёт скорости в точке потока.
Рассмотрим наклонную трубу диаметром d, выделим живое сечение ω, в котором следует определить статический и полный напор по оси трубы (рис. 4.7).

Проведём произвольно плоскость сравнения 0-0 и отложим геометрический напор сечения z до оси живого сечения ω. Покажем пьезометр в живом сечении и отметим пьезометрический напор по уровню жидкости в пьезометре.

Таким образом, по показанию пьезометра определим статический напор (см. рис. 4.7):

Для определения полного напора по оси потока пользуются трубкой Пито (рис. 4.7). Это трубка очень малого диаметра с загнутым под углом 90˚ и гладко обработанным концом. Трубка Пито устанавливается по оси трубы или в любой другой точке потока так, чтобы скоростьuбыла направлена на входное отверстие трубки. При движении жидкости возникает скоростной напор в виде кинетической энергии .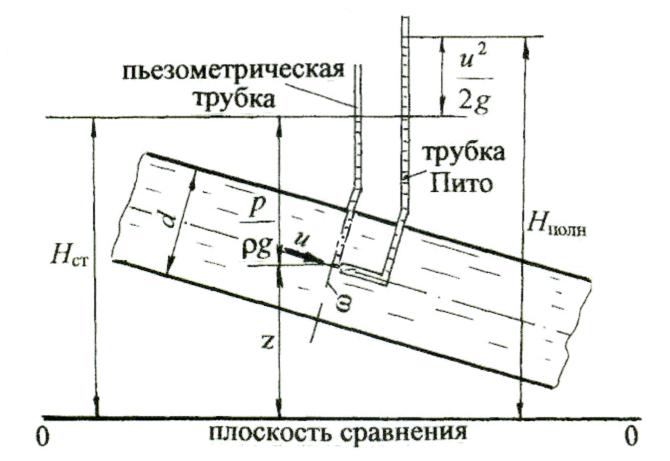


Рис. 4.7
При натекании жидкости на входное отверстие трубки Пито поток жидкости затормаживается, скорость на носике трубки становится равной нулю, а кинетическая энергия переходит в потенциальную энергию давления столба жидкости, а именно: горизонт воды в трубке Пито установится выше горизонта воды в пьезометре на величину .

Таким образом, трубкой Пито определяется полный напор Н_полнв заданной точке потока, в частности по оси потока (рис. 4.7).

Трубка Пито в сочетании с пьезометром является прибором для измерения скорости. Действительно, разность показаний трубки Пито и пьезометра соответствует скоростному напору:

отсюда скорость в точке потока: .

Для практических расчётов скорости пользуются формулой

, (4.16)

где φ – поправочный коэффициент, который определяется путём тарирования трубки Пито.

4.5.6. Диаграмма уравнения Бернулли для потока жидкости

в трубе переменного сечения

Рассмотрим экспериментальное построение диаграммы уравнения Бернулли для потока жидкости в трубе переменного сечения диаметрами d₁ , d₂ ,d₃ (рис. 4.8). Пусть d₂ < d₁ < d₃ . Для построения диаграммы воспользуемся принятой методикой (см. разделы 4.5.2; 4.5.3).

По направлению движения жидкости выделим три живых сечения - 1-1; 2-2; 3-3; выберем плоскость сравнения 0-0 и отложим геометрические высоты (напоры) выбранных сечений: z₁, z₂, z₃.

В сечениях покажем пьезометрические трубки. Как было отмечено выше (см. раздел 4.5.2), при сужении трубы пьезометрический напор понижается, а скоростной напор возрастает, и, наоборот, при расширении трубы пьезометрический напор повышается, а скоростной напор уменьшается. Перейдём к построению диаграммы для потока жидкости в трубе переменного сечения.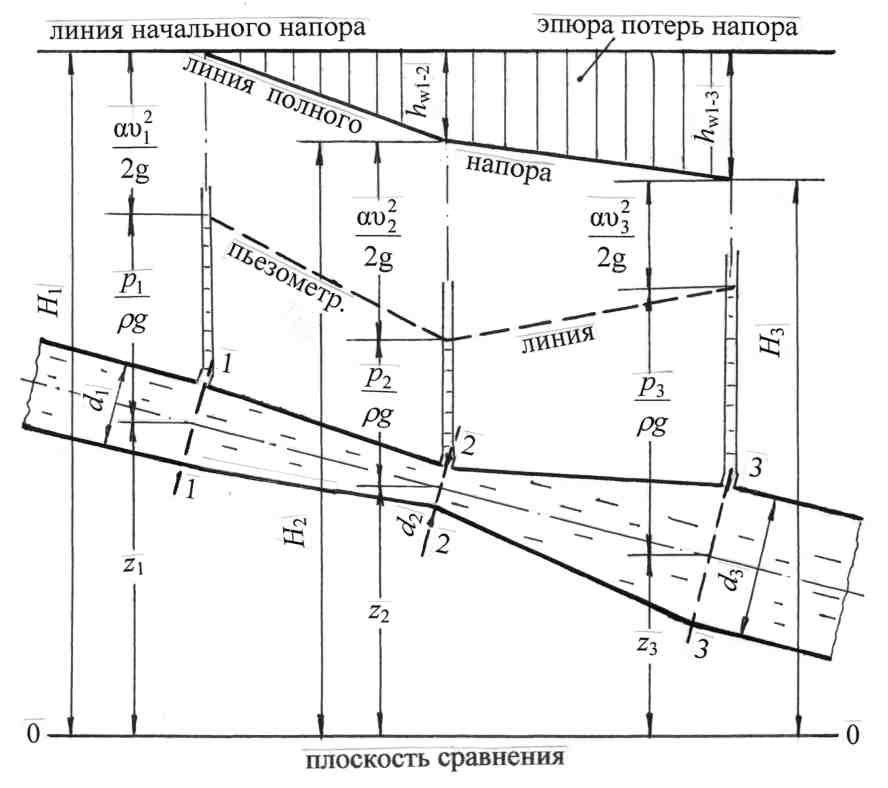



Рис. 4.8

В первом сечении к геометрическому напору z₁ прибавим пьезометрический напор , покажем уровень жидкости в пьезометре, затем прибавим по вертикали скоростной напор в первом сечении , сумму трёх напоров в первом сечении обозначим, как полный напор в первом сечении Н₁.

От значения полного напора в первом сечении Н₁ проведём линию начального напора (см. рис. 4.8).

Во втором сечении от линии начального напора по вертикали вниз откладываем потери напора между первым и вторым сечениями , затем скоростной напор > , на диаграмме получаем, что пьезометрический напор при сужении трубы понижается.

Показываем уровень жидкости во втором пьезометре. Обозначаем полный напор во втором сечении Н₂ (см. рис. 4.8).

Аналогичные построения проводим для третьего живого сечения.

От линии начального напора откладываем по вертикали вниз потери напора между первым и третьим сечениями , затем скоростной напор в третьем сечении: ,

учитывая, что d₃ > d₁ > d₂.

Обозначим уровень жидкости и пьезометрический напор в третьем сечении , при увеличении площади живого сечения пьезометрический напор повышается. Покажем полный напор в третьем живом сечении Н₃.

Проведём пьезометрическую линию по уровням жидкости в пьезометрах (рис. 4.8).

Анализ построения пьезометрической линии показывает, что пьезометрическая линия очерчивается ломаной линией, которая может повышаться или понижаться в зависимости от геометрических размеров трубы.

Соединяем ломаной линией значения полных напоров - это линия полного напора (см. рис. 4.8).

Линия полного напора по ходу движения жидкости понижается. Понижение линии полного напора соответствует величине потерь напора между сечениями по ходу движения жидкости: соответственно - потери напора между первым и вторым сечениями; - потери напора между первым и третьим сечениями.

Вертикальными линиями, проведёнными от линии полного напора до линии начального напора, заштриховываем эпюру потерь напора.

Построение диаграммы закончено.