гидравлика. !!ЛЕКЦ ЛАД ГИДР,2020. 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика

• Название: 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика
• Анкор: гидравлика
• Дата: 02.04.2021
• Размер: 1.61 Mb.
• Имя файла: !!ЛЕКЦ ЛАД ГИДР,2020.doc
• Тип: Документы; #190578
• страница: 7 из 9

6.3.1. Системы с последовательным соединением труб

Вначале рассмотрим простой случай сложной системы, состоящей из напорной башни с напором Н и трёх последовательно соединённых труб разного диаметра и разной длины с истечением жидкости в атмосферу (число участков может быть любым) (рис. 6.10).

Как отмечалось выше в разделе 6.3, расчёт такой системы можно провести, пользуясь уравнением Бернулли для двух сечений: по свободной поверхности жидкости в напорной башне и на выходе жидкости в атмосферу (см. раздел 6.1.1). Путём рассуждений, приведённых в разделе 6.3, получим формулу (6.26) для действующего напора.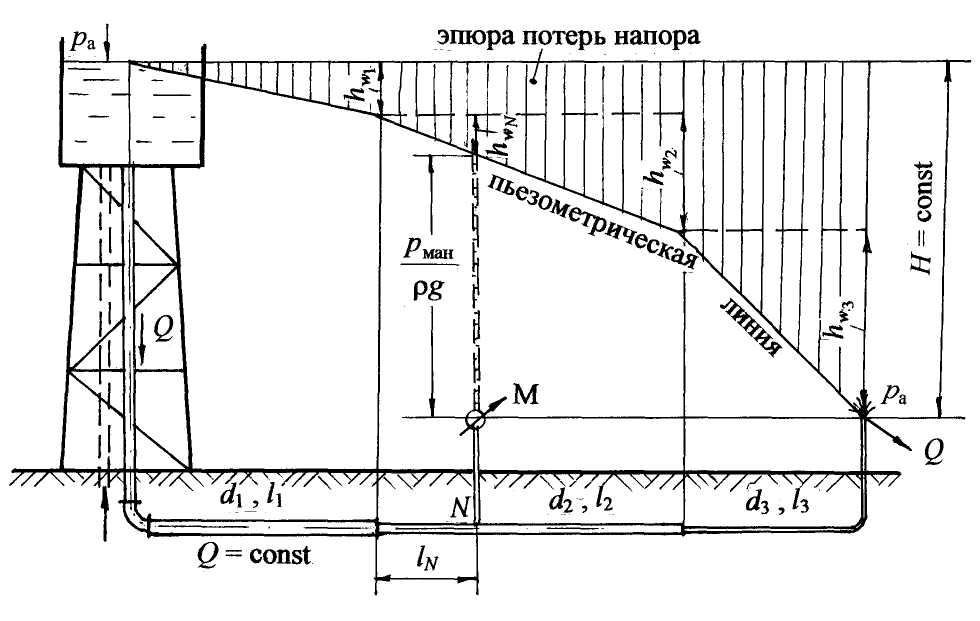


Рис. 6.10
Особенности расчёта системы

Пусть трубопроводная система не имеет промежуточных (путевых) потребителей. Пользуемся принятой методикой расчёта сложных систем (см. раздел 6.3).

1. Распределение расхода. Ввиду отсутствия промежуточных потребителей по ходу движения жидкости, расход остаётся величиной постоянной, т. е. какое количество воды поступает из напорной ёмкости, такое же количество истекает в атмосферу у потребителя, следовательно, Q= const.

2. Потери напора по длине при последовательном соединении труб рассчитываются, как сумма потерь напора на отдельных участках:

.

3. Действующий напор определяется по формуле (6.26):

(6.27)

или с учётом формулы (5.21): h_l= AQ²l при постоянном расходе:

(6.28)

где А₁, А₂, А₃ - удельное сопротивление трубопровода, принимается по табл. 9 (см. приложение) в соответствии с диаметрами d₁,d₂,d₃;

l₁,l₂,l₃ – длины участков трубопроводов.

4. Строится пьезометрическая линия на основном чертеже(рис. 6.10) аналогично построению пьезометрической и напорной линии для простой системы (рис. 6.5). При построении пьезометрической линии нужно учитывать не только потери напора по длине, но и потери в местных сопротивлениях, поэтому на каждом участке покажем .

Проектируем начало трубопровода на свободную поверхность в башне, из конца каждого участка трубопровода проводим вертикальные линии. Откладываем потери напора на первом участке , изменение потерь напора подчиняется линейному закону, так как длина трубы входит в формулу потерь напора (5.21) в первой степени. К потерям напора на первом участке прибавляем потери напора на втором ( ) и на третьем ( ) участках. В сумме потери напора равны действующему напору, т. е. весь действующий напор Н идет только на преодоление сопротивлений в системе, затратой напора на создание скорости при истечении в атмосферу пренебрегаем (см. раздел 6.3).

Вертикальными штриховыми линиями показываем эпюру потерь напора.

5. Пусть дополнительно требуется определить показание манометра р_ман, установленного на расстоянии l_N от начала второй трубы.

Покажем геометрическое определение потерь напора до точки N.

Из точки N проводим вертикальную линию. На эпюре потерь напора находим потери напора до точки N( ). В месте установки манометра можно показать пьезометр (пунктирная линия). Показание пьезометра соответствует .

Рассмотрим аналитический расчёт манометрического давления в точке N: ,

далее , (6.29)

из формулы (6.29) определим показание манометра в точке N.

2. 
   Системы с параллельным соединением труб
   

Системы с параллельным соединением труб - это системы, в которых магистральный трубопровод в некоторой точке разветвляется на несколько труб разных длин и разных диаметров, затем трубы вновь объединяются в магистральный трубопровод того же или другого диаметра. Эти системы называются также кольцевыми, т. е. закольцовано несколько труб. Преимущество таких систем состоит в том, что обеспечивается надёжность и бесперебойность работы системы (например, одна из ветвей может быть резервной), а также включение труб меньшего диаметра при той же пропускной способности системы.

Рассмотрим кольцевую систему, представленную в плане. Известно манометрическое давление в начале магистрального участка, длины и диаметры всех участков (рис. 6.11).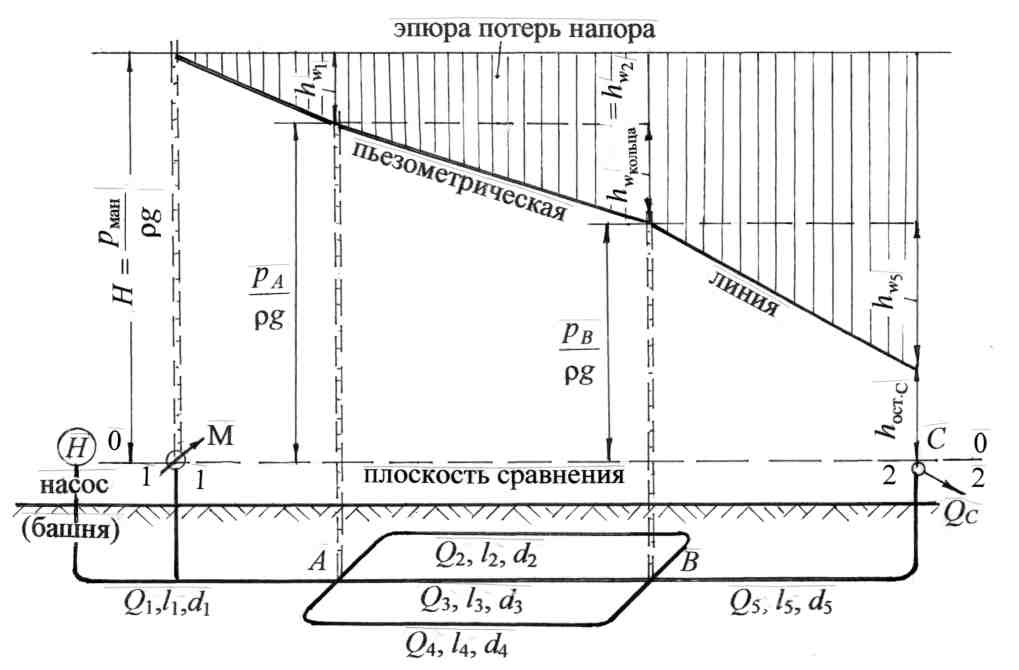


Рис. 6.11

Параллельно проложенные трубы разветвляются в точке А и соединяются в точке В, лежат на одном горизонте. Для наглядности параллельное соединение труб показано в изометрии. Пусть отсутствуют путевые потребители, а у конечного потребителя С должен быть остаточный (или свободный) напор

При расчёте сложных систем воспользуемся уравнением Бернулли.

1. Выбираем два сечения: одно в месте установки манометра, другое -на выходе воды у потребителя С.

2. Сечения нумеруем по направлению движения воды: 1 – 1 - в месте установки манометра; 2 - 2 – на выходе воды у конечного потребителя С.

3. В выбранных сечениях учитываем абсолютное давление, т. е. рассчитанное с учётом атмосферного: р₁ = р_а + р_ман; р₂ = р_а + .

У потребителя С мысленно можно представить пьезометр, показание которого h_ост.С (рис. 6.9).

Скорости воды в выбранных сечениях одинаковы: υ₁ = υ₂ = υ, но для сложных длинных систем скоростным напором можно пренебречь (см. раздел 6.3).

4. Плоскость сравнения обозначим 0 – 0 (см. пунктирную линию).

5. Запишем уравнение Бернулли в общем виде и подставим параметры:

;

z₁ = 0; z₂ = 0;

p₁ = p_а + р_ман р₂ = р_а + ρgh_ост.С

υ₁ = υ₂ = υ; α₁ = α₂ = 1,0

После преобразований: .

Обозначим = Н, где Н – действующий напор.

Тогда . (6.30)

Прочитаем формулу (6.30): действующий напор Н, создаваемый насосом, затрачивается на преодоление гидравлических сопротивлений в системе и создание остаточного напора у потребителя h_ост.С).

В месте установки манометра пунктиром покажем пьезометр и действующий напор Н (рис. 6.11).

Особенности расчёта системы с параллельным соединением труб.

1. Распределение расхода. На каждом участке введём обозначение расхода с индексом, соответствующим диаметру: Q₁, Q₂, Q₃, Q₄, Q₅. При отсутствии потребителей по длине системы и наличии только одного конечного потребителя с расходом Q_C расход на магистральном участке равен сумме расходов в параллельных ветвях трубопроводов:

Q₁ = Q₂ + Q₃ +Q₄. (6.31)

На пятом магистральном участке Q₅ = Q₁, а также Q₅ = Q_C .

2. Потери напора в системе. При параллельном соединении труб давление, а следовательно, и пьезометрический напор в точках разветвления А и В одинаковы для любого из параллельных участков.

На рис. 6.11 пунктирными линиями показаны пьезометры в точках А и В, а также пьезометрические напоры и .

В главе 5 отмечалось, что потери напора в гидравлических сопротивлениях определяются, как разность показаний пьезометров в начале и в конце участков сопротивлений, следовательно, потери напора в кольце равны потерям напора по любому из параллельных участков:

;

. (6.32)
Из равенства потерь напора в параллельных участках трубопроводов можно найти распределение расходов по ветвям в кольце. Приравняем потери по длине, т. е. в формуле (6.32) не учитываем поправочный коэффициент на местные сопротивления: , (6.33)

или с учётом формулы (5.21): . (6.34)

Расходы воды в параллельных трубопроводах рассчитаем по следующей методике: из формулы (6.34) выразим Q₃ через Q₂, затем Q₄ через Q₂. Подставив значения Q₃ и Q₄, выраженные через Q₂, в формулу (6.31), получим уравнение с одним неизвестным Q₂ (при условии, что Q₁ задано). Определим Q₂, затем Q₃ и Q₄.

Итак, приравняем: ,
выразим Q₃ через Q₂: ; (6.35)

приравняем: ,

выразим Q₄ через Q₂: . (6.36)

Подставим значения Q₃ и Q₄ в формулу (6.31):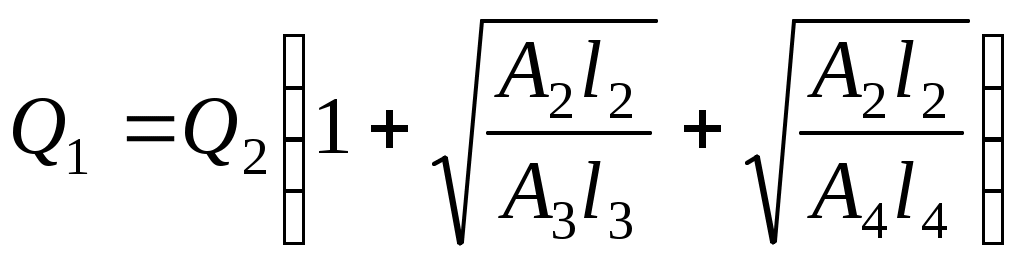

, (6.37)

получим Q₂, выраженное через Q₁: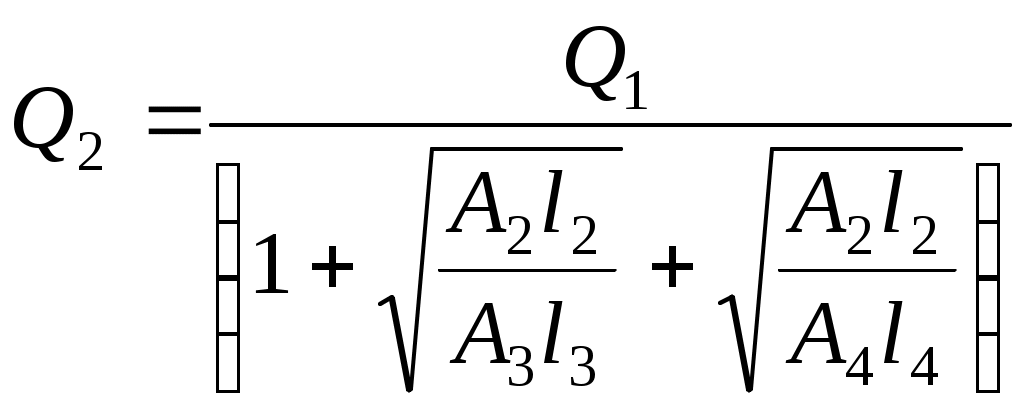

, (6.38)

затем по формулам (6.35) и (6.36) определим Q₃ и Q₄.

При расчётах формула (6.38) математически становится очень простой, т.к. и

представляют собой простые числа: длины участков заданы, значения коэффициентов Ав соответствии с диаметром трубы принимаются по табличным данным.

Таким образом, рассмотрены два самых важных момента при расчёте кольцевых систем: расход на магистральном участке равен сумме расходов в параллельных ветвях; потери напора в параллельных участках равны.

3. Действующий напор для представленной кольцевой системы с учётом гидравлических сопротивлений (h_w)

h_w = Σh_r + h_l = (1,05 1,1) h_l ,

где коэффициент (1,05 1,1) учитывает потери напора в местных сопротивлениях:

. (6.39)

Прочитаем формулу (6.39): действующий напор должен быть таким, чтобы преодолеть сопротивление в системе и обеспечить остаточный напор у потребителя С. Формула (6.39) аналогична формуле (6.30), полученной из уравнения Бернулли.

Учтём потери напора в кольце, например, по второму участку кольца введём в формулу (6.39) расходы:

. (6.40)

Следует помнить, что .

4. На схеме установки (см. рис. 6.11) строим пьезометрическую линию и эпюру потерь напора по аналогии с системой последовательно соединённых труб (см. рис. 6.10).
6.3.3. Распределительные сети, или тупиковые системы

Это сложные системы, состоящие из разветвлённой сети трубопроводов, имеющие несколько конечных потребителей. Как правило, известно, какими расходами следует обеспечить потребителей, а также какой должен быть остаточный (свободный) напор у потребителя или на какую отметку следует поднять воду у потребителя. При известном расходе ставится также задача подобрать диаметры трубопроводов.

Тупиковые системы принято представлять в плане. Рассмотрим принцип расчёта тупиковой водопроводной системы на примере системы, представленной на рис. 6.12.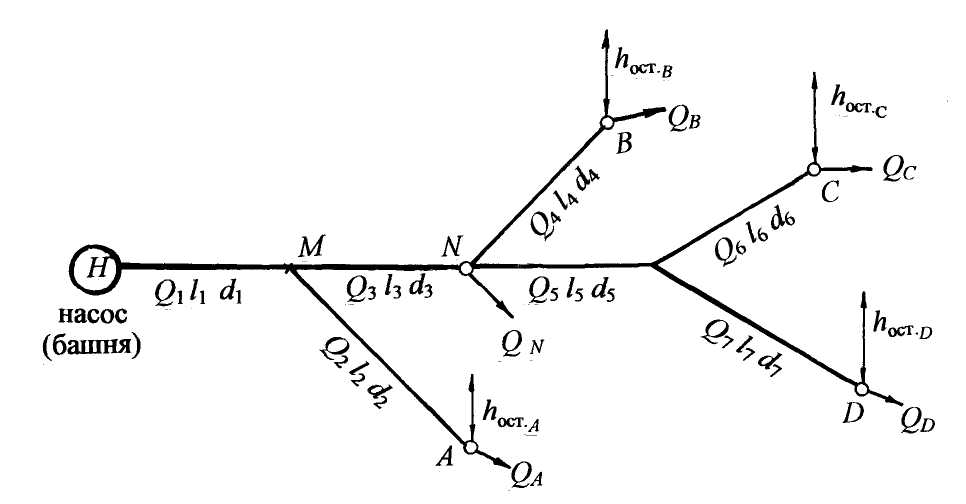


Рис. 6.12
. Система имеет четыре конечных потребителя (A, B, C, D) и один промежуточный потребитель в точке N по пути движения воды. Остаточные напоры (или высота подъёма) воды у конечных потребителей различные ( ).

Согласно принятой методике расчёта сложных систем (см. раздел 6.3), покажем особенности расчёта тупиковых систем.

1. Распределение расхода. Расход на каждом участке представим через расходы потребителей. Помним, что на магистральном участке расход равен сумме расходов потребителей. Первый участок является магистральным для всех потребителей:

Q₁ = Q_A + Q_N + Q_B + Q_C + Q_D, а также Q₁ = Q₂ + Q₃.

На третьем участке:

Q₃ = Q_N+ Q_B + Q_C + Q_D; а также Q₃ = Q_N + Q₄ + Q₅.

На пятом участке: Q₅ = Q_C + Q_D ; а также Q₅ = Q₆ + Q₇ .
На отдельных участках, ведущих к потребителю, расход равен расходу потребителя: Q₂ = Q_A; Q₄ = Q_B ; Q₆ = Q_C ; Q₇ = Q_D .

2. Потери напора по длине любого из направлений рассчитываются из условия последовательного соединения труб, т. е. суммируются. Для рассматриваемой схемы (см. рис. 6.12) потери напора до потребителя А:

,

до потребителя В: ,

до потребителей CиDсоответственно:

;

.

Потери напора с учётом местных сопротивлений по любому направлению: . (6.41)

3. Потребный действующий напор Н, или высота водонапорной башни, определяется по максимальной величине суммы потерь напора и остаточного напора по одному из направлений. В частности, для представленной схемы (см. рис. 6.12) действующий напор:

, (6.42)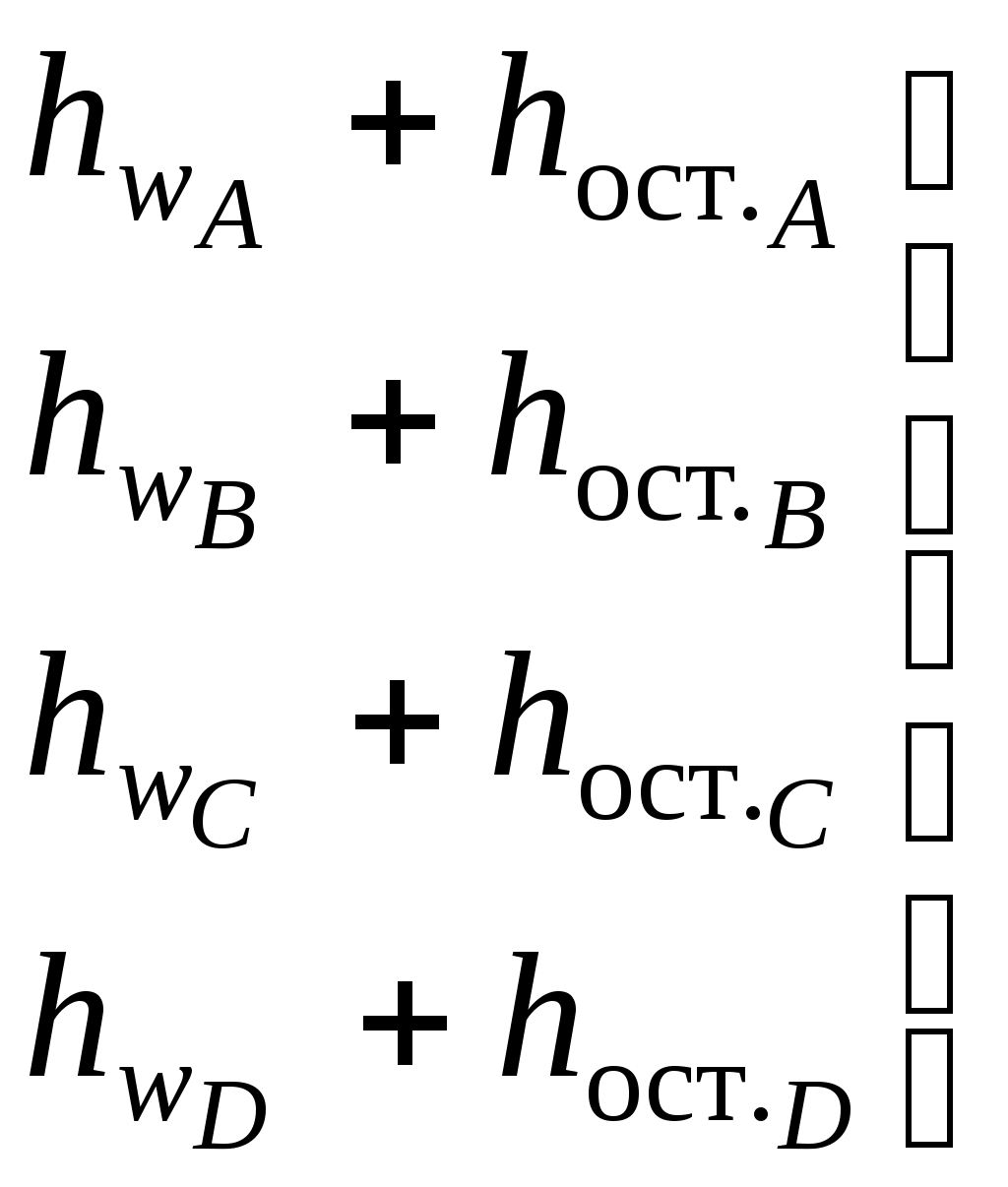

где сравниваем, из них выбираем максимальную величину:

т. е. .

4. Дополнительным условием в задаче может быть расчёт диаметра трубопровода по заданному расходу потребителя, при этом рекомендуется эксплуатационная скорость в пределах υ_экс= (1,0 1,5) м/с.

Диаметр трубопровода на любом участке рассчитывается через расход:

. (6.43)

По окончании расчёта, как правило, строится пьезометрическая линия.

Решение задачи для тупиковой водопроводной системы с построением пьезометрической линии приведено в разделе 6.4.2.