гидравлика. !!ЛЕКЦ ЛАД ГИДР,2020. 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика
 Скачать 1.61 Mb.
|
|
Системы с путевым расходом жидкости Эти системы включают трубопровод, в котором жидкость раздаётся в ряде пунктов по его длине. При большом количестве таких пунктов с достаточной точностью можно считать, что расход жидкости распределяется равномерно по длине l с интенсивностью q = Qпут/l. Такие трубопроводы называются также трубопроводами с равномерной раздачей жидкости. Наиболее характерным является случай, когда в трубопроводе кроме равномерного путевого расхода Qпут = ql имеется транзитный расход Qтр, проходящий по трубе и забираемый в конце трубопровода (рис. 6.13). При этом общий расход жидкости, поступающий в трубопровод: Q= Qтр + Qпут = Qтр + ql. 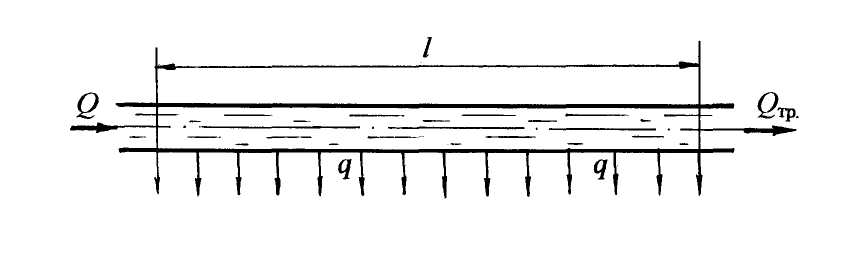 Рис. 6.13 Основным вопросом для систем с путевым расходом является определение величины потерянного напора. Общие потери по длине трубопровода с учётом путевого и транзитного расходов можно определить по формуле:  , (6.44)где А – удельное сопротивление для заданного диаметра трубы, принимается по табл. 8 (см. приложение). 6.5. Особенности гидравлического расчёта металлопластиковых труб Кроме металлических труб в промышленных, жилых, общественных и административных системах водоснабжения используют металлопласти-ковые, а также пластмассовые трубы из полиэтилена, поливинилхлорида, винипласта и им подобные. Особое внимание уделим металлопластиковым трубам (МПТ). Странами-производителями являются Китай, Германия, Нидерланды, Великобритания, Бельгия. Металлопластиковые трубы сочетают в себе преимущества пластмассы и металла. Они представляют собой пятислойную конструкцию, где три основных слоя и два связующих. Внутренний слой трубы произведён из сшитого полиэтилена (РЕ-Хс) методом экструзии гранулированного полиэтилена высокой прочности (HDPE). На поверхность наносится слой специального клея, соединяющий полиэтилен с алюминием. На поверхность алюминия наносится ещё один слой специального клея, связывающий алюминий с внешним слоем пластика РЕ-Хс. Вся труба сшита посредством бомбардировки электронами как внутреннего, так и внешнего слоёв. Алюминиевый слой армирует металлопластиковую трубу. Для их прокладки не нужны сварочные аппараты, трубогибы, муфты, уголки и т. п. Эти трубы абсолютно не подвержены коррозии, химическим и электрохимическим воздействиям, не засоряются, в них не образуются отравляющие воду окиси, как в медных, или ржавая грязь, как в стальных, даже из нержавеющей стали. Их гидравлическое сопротивление значительно ниже иных видов труб, ввиду малой шероховатости. Срок службы металлопластиковых труб не менее 50 лет. Эти трубы остаются безупречны с точки зрения гигиены вне зависимости от срока службы. Единственное ограничение в использовании металлопластиковых труб: их нельзя использовать в открытых инженерных сооружениях, так как замёрзшая жидкость в трубах может привести к повреждению трубы. Металлопластиковые трубы имеют абсолютную шероховатость Δэ  0,007 мм, что в 10 раз ниже, чем у медных и латунных труб и в 20 раз ниже, чем у стальных труб.Можно считать движение воды в металлопластиковых трубах движением вдоль гладких стенок. Результаты исследований, проведённых Ф. А. Шевелёвым во ВНИИ ВОДГЕО, показали, что коэффициент гидравлического сопротивления λ (коэффициент Дарси) следует рассчитывать по формуле: λ = 0,25/Re0,226. (6.53) Значения коэффициента λ по формуле (6.53) близки к значениям λ по формуле (5.11) Блазиуса: λ = 0,3164/Re0,25. Вместе с этим следует отметить, что в отличие от расчётов коэффициента λ по формуле Блазиуса, для металлопластиковых труб значения коэффициентов λ более низкие. Это значит, что такие трубы имеют большую пропускную способность. Стандартные металлопластиковые трубы имеют наружные диаметры: dнаруж = 14; 16; 20; 26; 32; 40; 50; 63, мм; с толщиной стенок δ = (2  4,5) мм.Предлагается при гидравлических расчётах принимать значения коэффициентов местных сопротивлений: при внезапном расширении ζв.р = 1,0; при внезапном сужении ζв.с = 0,5; тройники для разделения и слияния потоков ζтройн = 4,3 0,7;отвод под углом α = 90º ζотв = 4,2 0,5;переходные муфты ζмуфт = 4,2 0,5;фитинг (прямой переходник) ζперех = 2,5 0,1.Большие значения коэффициентов местных сопротивлений принимаются для меньших диаметров труб. Коэффициенты сопротивлений запорных устройств (краны, вентили) принимаются в соответствии с характеристиками таких устройств. Следует отметить преимущества металлопластиковых труб: - прочны, как металлические, и пластичны, как полимерные; - пригодны для сложной геометрической укладки; - надёжны и долговечны; - гигиеничны в использовании; - просты в эксплуатации; - допустимо максимальное рабочее давление 10 бар. 7. Истечение жидкости из отверстий и насадков. В инженерной практике часто встречаются случаи истечения жидкости через отверстия и насадки, представляющие собой короткие патрубки различной конфигурации. Путём расчёта истечения жидкости из отверстий и насадков решаются такие технические задачи, как измерение количества проходящей жидкости, создание сильной дальнобойной и компактной струи, распространение свободной струи, конструирование сопл и форсунок и др. Истечение может происходить при постоянном или переменном напоре. В первом случае движение жидкости считается установившимся. Истечение жидкости может происходить в атмосферу и называется свободным истечением, а также в другой резервуар, заполненный жидкостью. Такое истечение называется истечением под уровень, или истечением через затопленное отверстие. Классификация отверстий 1. Малое отверстие в тонкой стенке (незатопленное и затопленное). 2. Малое отверстие в толстой стенке. Аналогом является короткий патрубок длиной l = (3  5)dотв (dотв – диаметр отверстия), присоединённый к малому отверстию.3. Большое отверстие в тонкой стенке. Малым считается отверстие, если разность напоров над верхней и нижней кромками отверстия не превышает 10 % вертикального размера отверстия. Действующий напор принимается по оси отверстия. В противном случае, если разность напоров над верхней и нижней кромками отверстия превышает 10 %, отверстие считается большим. При расчёте такого отверстия учитываются напоры над верхней и нижней кромками отверстия. Тонкой считается стенка, если толщина её δ не превышает трёх линейных размеров отверстия. Например, для круглого отверстия δ  3 dотв; для квадратного отверстия δ 3а (а – сторона квадрата).Толстой считается стенка, толщина которой δ = (3 5)dотв. Если толстую стенку убрать, оставить только ограничение, например, в виде патрубка, то такой патрубок называется гидравлическим насадком.Итак, гидравлический насадок – это короткий патрубок длиной l = (3 5)d, присоединённый к малому отверстию в тонкой стенке.Если длина патрубка l> 5d, то такое движение жидкости следует рассматривать как движение в короткой трубе. Рассмотрим теоретические основы расчета истечения жидкости через отверстия и насадки. 7.1. Истечение жидкости из малого незатопленного и затопленного отверстий в тонкой стенке Под расчётом отверстия понимается определение пропускной способности отверстия, или расхода Q. Рассмотрим малое отверстие в тонкой стенке закрытого резервуара, на поверхности жидкости в котором действует абсолютное давление р0, в общем случае не равное атмосферному (рис. 7.1). 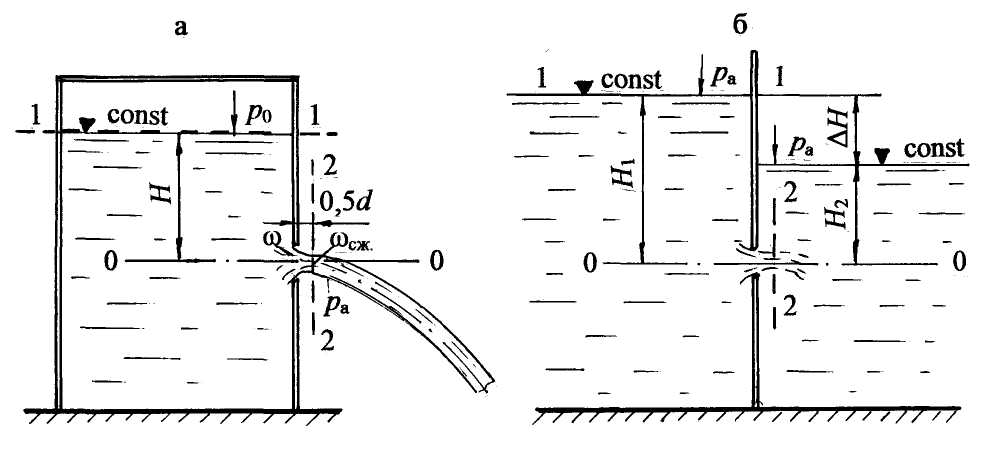 Рис. 7.1 Площадь живого сечения отверстия ω, действующий напор по оси отверстия Н, уровень воды в резервуаре постоянный. При истечении жидкости через малое отверстие на расстоянии 0,5d происходит сжатие (инверсия) струи. Это явление объясняется инерцией частиц жидкости, параболической траекторией струек в потоке, которые пересекаются, уменьшая при этом сечение. В сжатом сечении (площадь ωсж) движение жидкости можно считать установившимся и применить для него уравнение Бернулли. Для определения расхода жидкости через малое незатопленное отверстие, т. е. свободное истечение в атмосферу, используем уравнение Бернулли, согласно принятой методике (см. раздел 4.5.7). 1. Выберем два сечения: по свободной поверхности жидкости в резервуаре (проведём его горизонтально, здесь скорость υ = 0) и на выходе струи в атмосферу по сжатому сечению, это сечение проведём нормально к направлению движения струи. 2. Сечения 1-1 и 2-2 пронумеруем по направлению движения жидкости. 3. В выбранных сечениях учтём абсолютное давление. Подчеркнём, что давление в сжатом сечении равно атмосферному (выход жидкости в атмосферу): р1 = р0; р2 = ра . 4. Плоскость сравнения 0-0 проведём через ось отверстия, тогда z1 = H; z2 = 0. 5. Запишем уравнение Бернулли (см. формулу (4.15)) в общем виде и сделаем подстановку параметров:  ;z1 = H; z2 = 0; p1 = p0; p2 = pa; υ1 = 0; υ2 = υсж; α2 = αотв, где αотв – коэффициент неравномерности распределения скорости в отверстии. Потери напора по длине между сечениями 1-1 и 2-2 (расстояние 0,5d) отсутствуют, значит, потери напора в гидравлических сопротивлениях hw учтём, как потери напора в самом отверстии, как местном сопротивлении:  ,где ζотв – коэффициент сопротивления отверстия. После подстановки параметров получим:  ,откуда скорость в сжатом сечении: 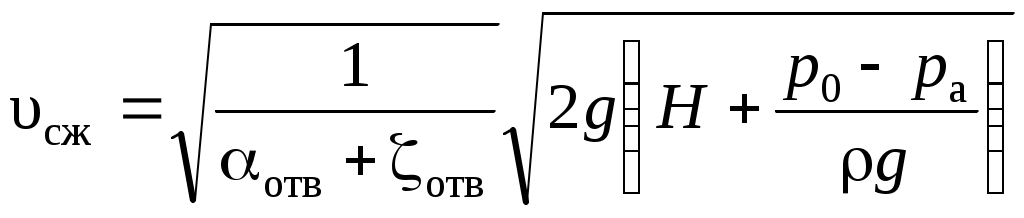 . (7.1)В формуле (7.1) обозначим приведённый напор (Нприв):  Если резервуар будет открытым, в сечении 1-1 давление р1 = ра, то приведённый напор Нприв = Н. Формулу (7.1) представим в виде  . (7.2)Введём коэффициент скорости (φ):  . (7.3)Формула (7.2) принимает вид:  . (7.4)При расчёте расхода Q (или пропускной способности) из отверстия нужно скорость в сжатом сечении умножить на площадь сжатого сечения: Q= υсж ωсж . Уменьшение площади сжатого сечения учитывается коэффициентом сжатия ε:  . (7.5)Расчётная формула для расхода с учётом формул (7.4) и (7.5):  . (7.6)Произведение коэффициентов εφ называется коэффициентом расхода отверстия, обозначим его через μотв: μотв = εφ. Окончательно расход жидкости через малое незатопленное отверстие рассчитаем по формуле:  . (7.7)Рассмотрим малое затопленное отверстие в тонкой стенке, или истечение из малого отверстия под уровень (рис. 7.1, б). Расчёт аналогичен расчёту малого отверстия в тонкой стенке с истечением в атмосферу. Так же составляется уравнение Бернулли для сечений 1-1 и 2-2, скорости в которых соответственно: υ1 = 0; υ2 = υсж.; давления в выбранных сечениях: р1 = ра; р2 = ра + ρgH2; плоскость сравнения совмещается с осью отверстия:  ;  .После преобразования уравнения Бернулли  . (7.8)Можно обозначить Н1 – Н2 = ΔН; таким образом, ΔН – действующий напор для затопленного отверстия. Расход жидкости через затопленное отверстие:  . (7.9)Формулы (7.7), (7.9), а ранее при расчёте простых трубопроводных систем формула (6.5) имеют общий вид. Таким образом, для всех видов истечений из отверстий, а также для насадков формула расхода может быть представлена обобщённой формулой:  , (7.10)где Н – действующий (или приведённый) напор; μ - коэффициент расхода. 7.2. Истечение жидкости через большое боковое отверстие при постоянном напоре Представим себе большое боковое отверстие прямоугольной формы, ширина которого b, напор над верхней кромкой отверстия Н1, над нижней Н2.  . (7.11)(Пусть напоры над верхней и нижней кромками отверстия отличаются более чем на 10 %, тогда в формуле расхода учитываем оба напора). Теоретический вывод формулы (7.11) следует изучить по учебникам и другим учебным пособиям. 7.3. Истечение жидкости из насадков при постоянном напоре По форме патрубка различают следующие типы насадков: а) внешний цилиндрический насадок (рис. 7.2, а); б) внутренний цилиндрический насадок (рис. 7.2, б); в) конический сходящийся насадок (рис. 7.2, в); г) конический расходящийся насадок (рис. 7.2, г); д) коноидальный насадок (рис. 7.2, д). Во всех типах насадков, кроме коноидального, внутри насадка, как правило, на расстоянии 0,5dобразуется сжатие струи. В области сжатия возникает вакуум, затем струя расширяется, заполняя весь насадок, и выходит полным сечением. Вакуум внутри |