гидравлика. !!ЛЕКЦ ЛАД ГИДР,2020. 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика

• Название: 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика
• Анкор: гидравлика
• Дата: 02.04.2021
• Размер: 1.61 Mb.
• Имя файла: !!ЛЕКЦ ЛАД ГИДР,2020.doc
• Тип: Документы; #190578
• страница: 6 из 9

«ПРИКЛАДНАЯ ГИДРАВЛИКА, ГИДРОМЕХАНИКА»
6. Гидравлический расчет трубопроводных систем.
По методике расчёта трубопроводные системы делят на две группы – простые и сложные.

Простые системы состоят, как правило, из одной трубы, возможно соединение нескольких труб сравнительно небольшой длины (примерно до 100 м), в которых учитываются все виды гидравлических сопротивлений, но, главное, с постоянным расходом.

Сложные системы состоят из труб разной длины и разных диаметров, соединённых по определённой гидравлической схеме, причём расход жидкости на каждом участке различный - в соответствии с расходами потребителей. Эти системы, как правило, большой длины. Главными гидравлическими сопротивлениями являются потери по длине. Потери напора в местных сопротивлениях принимаются равными (5 10) % от потерь напора по длине, т. е. Σh_r = (0,05 0,1) h_l .
6.1. Расчёт простых трубопроводных систем

При расчёте простых трубопроводов в зависимости от поставленной задачи, известных и определяемых параметров, выделяют три типа расчётов.

1. Определение напора Н или давления р при известных: расходе жидкости Q, геометрических размерах трубопровода (длине l, диаметре d), местных сопротивлениях на трубопроводе.

2. Определение расхода Q, или пропускной способности трубопровода, при известных: действующем напоре Н или давлении р в системе; геометрических размерах и установленных местных сопротивлениях.

3. Определение геометрических размеров трубопроводов (l; d), характеристик местных сопротивлений при известном расходе Q, действующем напоре Н или давлении р.

Рассмотрим расчёт простого трубопровода. Здесь возможны два случая: истечение жидкости в атмосферу и истечение под уровень.

6.1.1. Расчёт простой трубопроводной системы

с истечением жидкости в атмосферу
На рис. 6.1 представлена схема простого водопровода с водонапорной башней, создающей постоянный напор Н.

Известны длина трубопровода l, диаметр d, местные сопротивления в виде входа в трубу, вентиля и двух колен (отводов). В представленной схеме действующий напор Н считается постоянным, уровень жидкости в напорном баке поддерживается на постоянном горизонте за счёт подачи воды (или другой жидкости) в бак, например, из скважины или от насосной установки, так, чтобы приток жидкости в бак равнялся расходу жидкости в системе.

Постоянная подача жидкости осуществляется по трубопроводу, обозначенному пунктирной линией.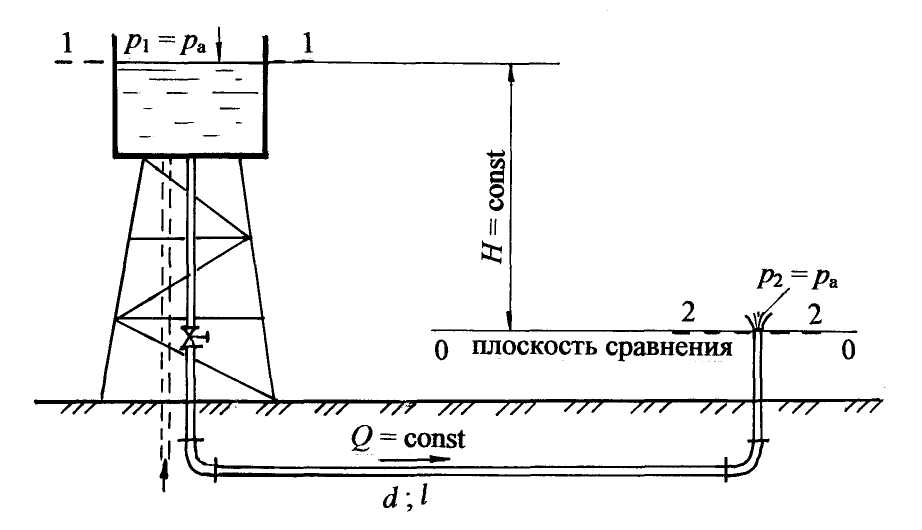

Рис. 6.1

В дальнейших схемах трубопроводных систем приток жидкости в систему не обозначается, но всегда подразумевается установившееся движение, т. е. скорость движения жидкости в трубе не изменяется во времени.

При расчёте простой системы с истечением в атмосферу воспользуемся уравнением Д-Бернулли (4.15).

1. Выбираем два сечения: одно сечение проводим по свободной поверхности в напорном баке (башне), где скорость допустимо считать равной нулю (уровень жидкости постоянный, движения нет), другое – на выходе жидкости из трубы, где существует определённая скорость движения.

2. Сечения 1-1 и 2-2 нумеруем по направлению движения жидкости.

3. В выбранных сечениях учитываем абсолютное давление, т. е. давление, рассчитанное с учётом атмосферного:

р₁ = р_а; р₂ = р_а.

4. Плоскость сравнения 0 – 0 совместим с сечением 2 – 2, тогда

z₁ = H; z₂ = 0. Если бы плоскость сравнения совместили с сечением 1 – 1, тогда z₁ = 0; z₂ = - H. Помним, что отсчёты от плоскости сравнения вверх считаются положительными, вниз – отрицательными.

5. Записываем уравнение Бернулли (4.15) в общем виде и указываем значение всех параметров: ;

z₁ = H;z₂ = 0;

p₁ = p_а; р₂ = р_а;

υ₁ = 0; υ₂ = υ; α₂ = 1,0;

для коэффициента α₂ предполагаем турбулентный режим в круглой трубе.

Получим:

В этом уравнении у потерь напора в гидравлических сопротивлениях h_w индекс 1-2 опускаем, поскольку вся расчётная схема системы находится между выбранными сечениями.

После сокращений получим: . (6.1)

Вывод: при истечении жидкости в атмосферу действующий напор затрачивается на создание скоростного напора и преодоление гидравлических сопротивлений.

Представим в уравнении (6.1) гидравлические сопротивления согласно формуле (5.1): h_w = Σh_r + h_l.

С учётом формул (5.2) и (5.3): и .

Получим

или . (6.2)

Таким образом, по формуле (6.2) рассчитывается действующий напор простой системы при истечении жидкости в атмосферу.

Из формулы (6.2) можно получить расчётную формулу для расхода.

Скорость движения жидкости в трубе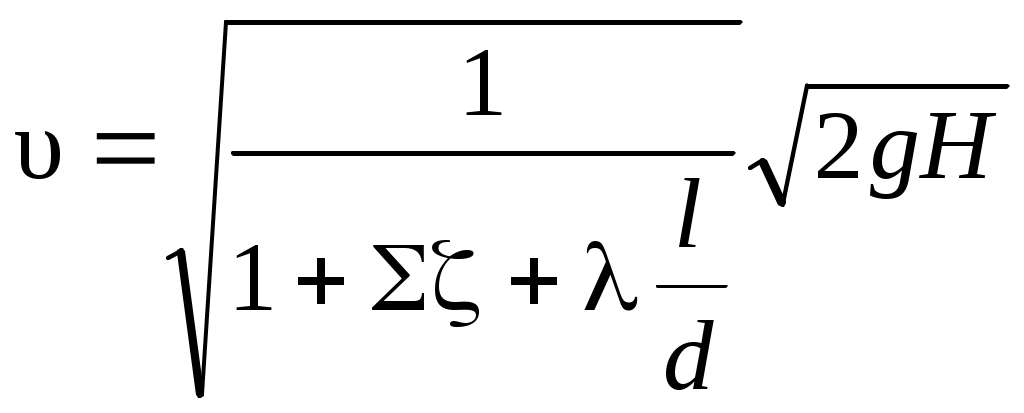

. (6.3)

Расход Q = υω, где ω – площадь живого сечения ( );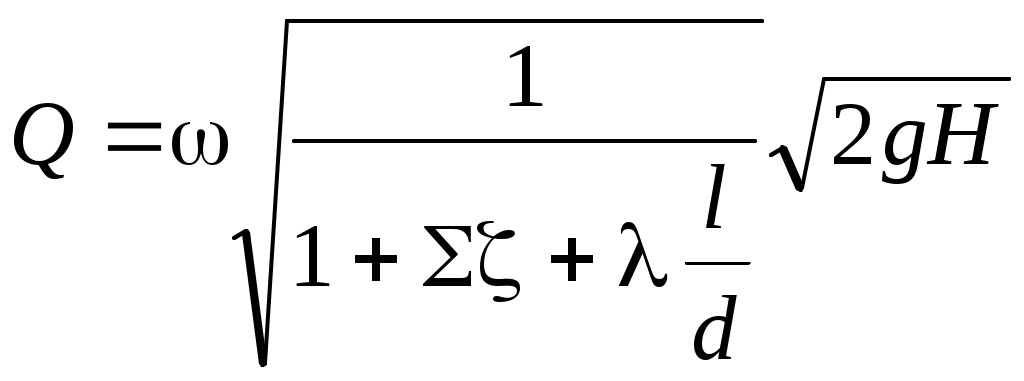

. (6.4)

В формуле (6.4) величина 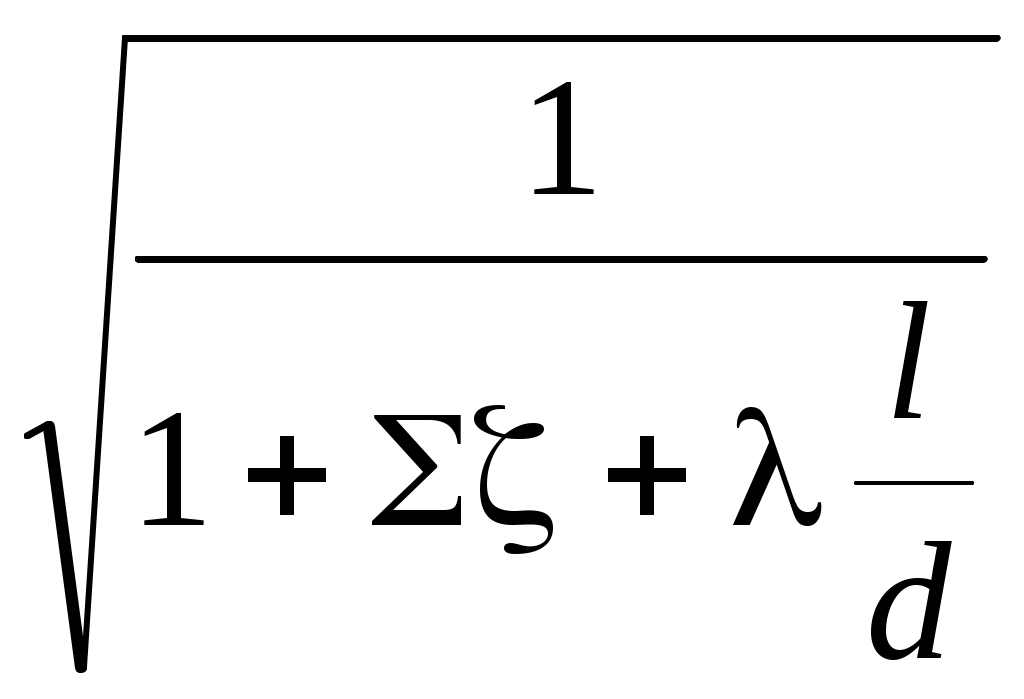постоянная для заданной системы, влияет на величину расхода и называется “коэффициентом расхода “, обозначается μ_сист : (6.5)

Формула (6.5) является обобщённой формулой для расхода жидкости в простых системах, а значение коэффициента μ рассчитывается для каждой системы.
6.1.2. Расчёт простой трубопроводной системы

при истечении жидкости под уровень
Истечением под уровень считается случай, когда жидкость поступает в резервуар, заполненный жидкостью, т. е. под уровень жидкости.

Схема трубопровода с истечением под уровень может быть получена из предыдущей схемы (см. рис. 6.1), но выход жидкости покажем в другой открытый резервуар (рис. 6.2).

Для расчёта простой системы с истечением под уровень воспользуемся уравнением Бернулли (4.15):

1. Выберем два сечения по свободным поверхностям жидкости в резервуарах, где скорости жидкости равны нулю.

2. Сечения 1-1 и 2-2 пронумеруем по направлению движения жидкости.

3. Учтём абсолютные давления в выбранных сечениях: р₁ = р_а; р₂ = р_а.

4. Плоскость сравнения 0-0 совместим с сечением 2-2, тогда

z₁ = H; z₂ = 0.

5. Запишем уравнение Бернулли в общем виде и покажем известные параметры: ;

z₁ =H; z₂ = 0;

р₁ = р_а; р₂ = р_а;

υ₁ = 0; υ₂ = 0.

После подстановки параметров и сокращений получим:

H =h_w. (6.6)

Вывод: в простой трубопроводной системе при истечении жидкости под уровень действующий напор затрачивается на преодоление гидравлических сопротивлений.

С учётом формул (5.1), (5.2) и (5.3) формула (6.6) принимает вид:

. (6.7)

Гидравлический расчёт двух рассмотренных систем аналогичен. Различие в формулах (6.2) и (6.7) состоит в том, что при истечении в атмосферу формула (6.2) учитывает скоростной напор υ²/2g на выходе, а в формуле (6.7) скоростной напор на выходе входит в потери напора при выходе жидкости в резервуар больших размеров, так как ζ_вых = 1,0.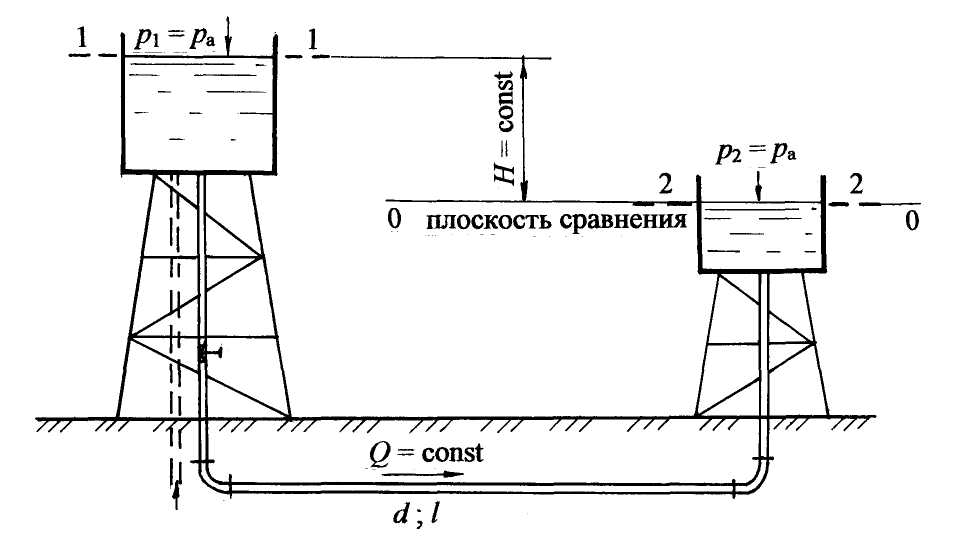


Рис. 6.2

По аналогии с предыдущим выводом получим формулу для расхода: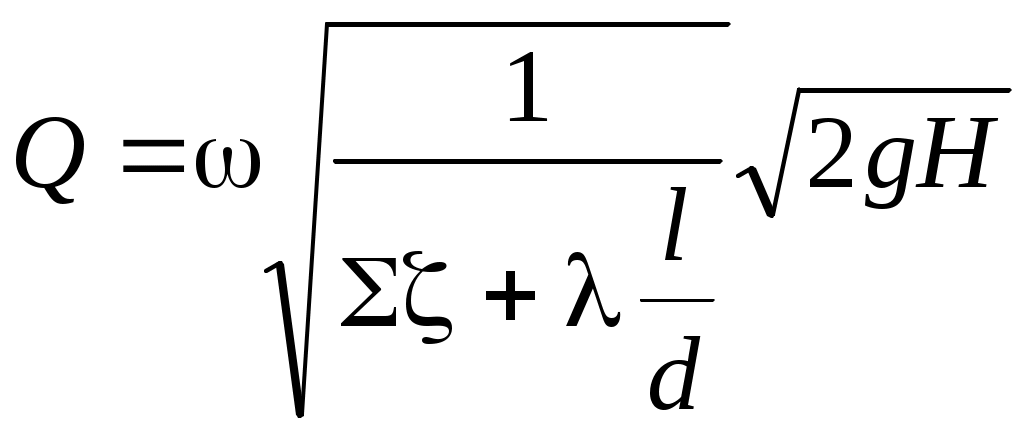

. (6.8)

Обозначим: 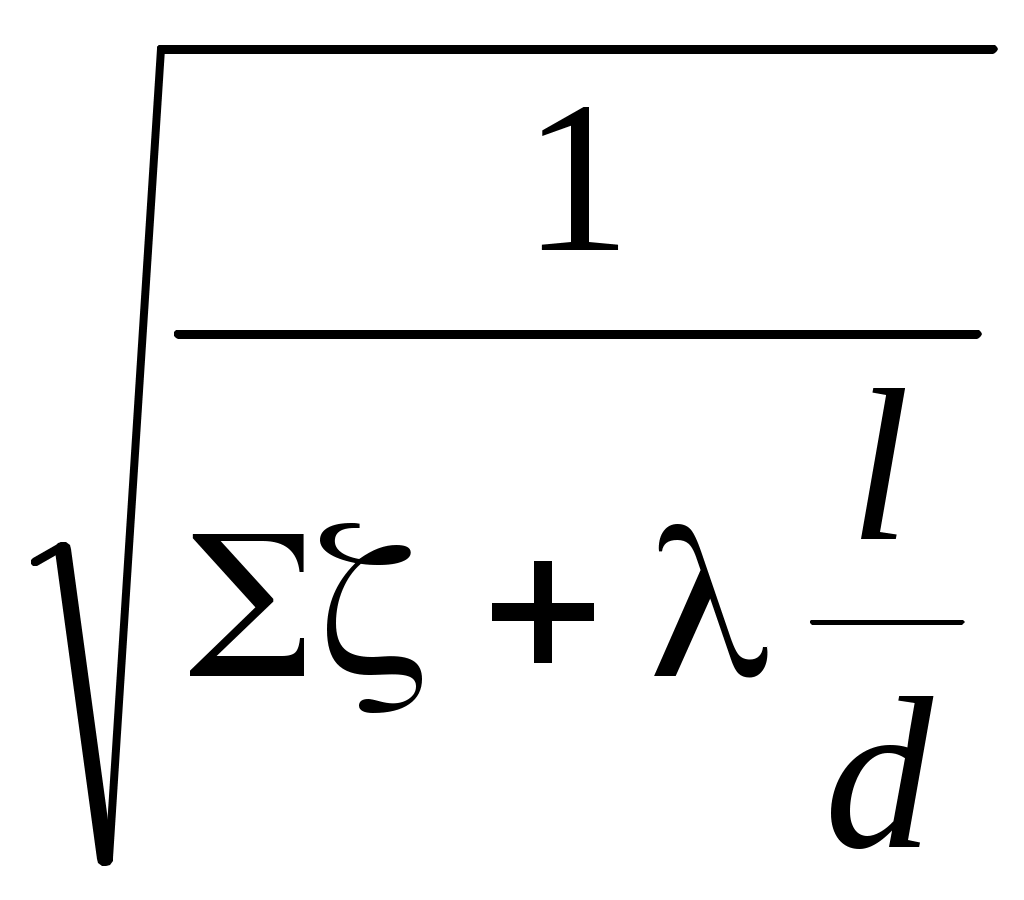= μ_{сист. под ур} ,

тогда Q= μ_{сист. под ур}ω . (6.9)

Формула (6.9) подтверждает обобщённость применения формулы (6.5).

На рис. 6.1 и 6.2 представлены схемы простых систем в самом общем виде.

В технике применяются различные схемы трубопроводных систем в виде водопроводов, нефтепроводов, газопроводов и им подобные. Движение жидкости происходит не только за счёт напорного бака (башни), разности напоров в резервуарах, но и за счёт давления, создаваемого насосом.


6.1.3. Методика расчёта простых трубопроводных систем.
Расчёт простых систем первого типа по определению напора Н или давления р включает следующие этапы:

1. 
   Составляется уравнение Бернулли для характерных сечений.
   

2. Производится подстановка всех параметров в буквенном выражении для определения неизвестного напора или давления.

3. Определяется скорость движения жидкости в трубе при известном расходе.

4. Рассчитываются потери напора в местных сопротивлениях Σh_r.

5. Определяются потери напора по длине h_l по схеме, представленной на рис. 5.1.

6. Производится численный расчёт напора или давления.
Простые системы второго типа по определению расхода Q рассчитываются в следующей последовательности:

1. 
   Составляется уравнение Бернулли для выбранных сечений.
   

2. Производится подстановка заданных параметров, и уравнение решается в буквенном выражении относительно скорости движения жидкости.

3. В расчётную формулу скорости входит коэффициент гидравлического сопротивления λ, формула для которого выбирается в соответствии со значением числа Рейнольдса Re. Но в формулу (4.20) для Re также входит неизвестная скорость, поэтому при заданной шероховатости трубы Δ_э при движении воды предполагается турбулентный режим, зона квадратичного сопротивления, для которой λ не зависит от числа Рейнольдса Re. Коэффициент λ рассчитывается по формуле Шифринсона (5.14), а затем определяется скорость движения жидкости.

4. Проверяется режим движения жидкости и зона сопротивления (см. схему на рис. 5.1). Если подтверждается квадратичная зона сопротивления, рассчитывается расход жидкости Q.

Если режим движения и зона сопротивления не подтвердится, проводится повторный расчёт коэффициента λ в соответствии с числом Re по схеме (см. рис. 5.1).

5. После окончательного уточнения режима движения и области сопротивления определяется коэффициент λ и рассчитывается расход Q.

Как правило, при движении воды в шероховатых трубах имеют место турбулентный режим, зона квадратичного сопротивления.

Расчёт простых систем третьего типа по определению длины или значений коэффициентов местных сопротивлений различных устройств (кранов, задвижек, диафрагм и им подобных) не представляет трудности.
6.3. Расчёт сложных трубопроводных систем
Сложные трубопроводы имеют разветвлённые участки, состоящие из нескольких труб, по которым распределяется жидкость в соответствии с расходами потребителей.

В зависимости от гидравлической схемы соединения трубопроводов различают:

- системы с последовательным соединением труб с одним конечным потребителем или с потребителями по ходу движения жидкости и также с одним конечным потребителем;

- системы с параллельным соединением труб, или кольцевые, также с одним или несколькими потребителями;

- распределительные сети, или тупиковые системы. Это системы с несколькими конечными потребителями;

- системы комбинированного типа, включающие участки трубопро-водных систем первых трёх видов;

- системы с непрерывной раздачей жидкости, их также называют системами с путевым расходом.

Как и при расчёте простых трубопроводных систем (см. раздел 6.1),

для сложных систем можно выделить три основных типа расчётов:

1) определение действующего напора Н; давления р в системе; разности напоров в питающем резервуаре и у потребителя при известном расходе Q, длинах и диаметрах трубопроводов отдельных участков;

2) определение расходов жидкости на отдельных участках и в целом в системе при известных геометрических размерах трубопроводов и напоре (или давлении);

3) определение геометрических размеров труб по заданным для них расходе и перепадах напора (давления).

При расчёте сложных трубопроводных систем по аналогии с простыми системами следует пользоваться уравнением Бернулли. Так, при истечении жидкости у потребителя в атмосферу (см. рис. 6.10) получим формулу (6.1)



Как правило, в сложных системах скоростным напором (υ²/2g) как малой величиной можно пренебречь. Действительно, эксплуатационная скорость в водопроводных системах υ_экс. = (1 1,5) м/c, реже до 2,0 м/с, значит, скоростной напор υ²/2g 0,12 м (очень малая величина по сравнению с действующим напором).

Таким образом, полный напор в любом расчётном сечении сложной системы практически равен гидростатическому напору, который представляется путём построения пьезометрической линии.

В сложных трубопроводных системах потери напора в местных сопротивлениях составляют (5 10) % от потерь напора по длине:

Σh_r = (0,05 0,1) h_l .

Тогда, согласно формуле (5.1): h_w = Σh_r + h_l = (1,05 1,1) h_l .

Формула (6.1) для действующего напора принимает вид:

(6.26)

где (1,05 1,1) – поправочный коэффициент на местные сопротивления;

- потери напора по длине в сложной системе, они представляются в соответствии с гидравлической схемой системы.

Потери напора по длине h_l на любом участке для сложных систем рассчитываются через расход Q (см. раздел 5.3.3) по формулам (5.19) или (5.21): или ,

где К, К², А – обобщённые параметры, которые принимаются по табл. 8 (см. приложение) в зависимости от диаметра трубопровода.

При решении задач по расчёту сложных трубопроводных систем рекомендуется пользоваться следующей методикой:

1. Рассматривается распределение расхода в системе. На каждом участке обозначается расход Q_i с индексом, соответствующим индексу диаметра трубопровода.

2. Представляются потери напора в системе, согласно схеме соединения труб.

3. По условию поставленной задачи определяются действующий напор, давление, разность напоров в питателе и у потребителя и подобные условия.

4. Дополнительно могут рассчитываться диаметр трубы при заданном расходе, свободный (остаточный) напор у потребителя, геодезическая отметка водонапорной башни или потребителя и тому подобное.

Рассмотрим особенности расчёта сложных трубопроводных систем с различными гидравлическими схемами.