гидравлика. !!ЛЕКЦ ЛАД ГИДР,2020. 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика

• Название: 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика
• Анкор: гидравлика
• Дата: 02.04.2021
• Размер: 1.61 Mb.
• Имя файла: !!ЛЕКЦ ЛАД ГИДР,2020.doc
• Тип: Документы; #190578
• страница: 3 из 9

«ГИДРОДИНАМИКА»
Основное уравнение гидродинамики. Режимы движения жидкости.
Гидродинамика – раздел, в котором изучаются законы движения жидкости, взаимодействие жидкости с твёрдыми поверхностями и движущимися твёрдыми телами. Раздел гидродинамики является основой для решения теоретических и инженерных задач по расчёту трубопроводных систем, открытых русел, истечения жидкости через отверстия и насадки.
4.1. Основные понятия о параметрах движения жидкости

К гидродинамическим характеристикам потока относят: гидродинамическое давление в точке жидкости р и действительная скорость движущейся частицы жидкости u.

В случае идеальной жидкости гидродинамическое давление р имеет тот же смысл, что и гидростатическое.

Что касается скорости, то она изменяется во времени и в пространстве. Математически такую зависимость трудно записать, поэтому гидродина-мические законы имеют достаточно общий характер с некоторыми допуще-ниями.

Скорость в точке потока или скорость в сечении элементарной струйки (понятие струйки будет приведено ниже) обозначается буквой u. Средняя скорость потока – υ.

В зависимости от того, являются ли основные параметры движения функцией времени, различают два вида движения жидкости: неустано-вившееся и установившееся.

Неустановившееся – это движение жидкости, при котором гидродинамические параметры давление и скорость являются функцией не только координат точки, но и времени.

Установившееся – это движение жидкости, при котором все параметры движения в одной и той же точке пространства не меняются во времени. Приращение скорости во времени (ускорение) равно нулю ( ).

В зависимости от характера изменения скорости по длине пространства, заполненного жидкостью, установившееся движение может быть:

а) равномерным, при котором скорость по длине струйки или потока остаётся постоянной. Примером является движение в трубах постоянного диаметра, в каналах правильной формы;

б) неравномерным, если скорость, глубина заполнения потока, форма сечения по длине потока изменяются по величине;

в) плавно изменяющимся, если изменение скорости происходит достаточно плавно (конические переходники, сужающиеся и расширяю-щиеся). В этом случае с достаточной для практики точностью применимы законы равномерного движения.

В программу данного курса входит изучение законов установившегося движения и применение этих законов для решения инженерных задач.
4.2. Понятие идеальной жидкости и потока жидкости

В разделе “Общие сведения о жидкостях” рассмотрены физические свойства жидкостей. В разделе “Гидродинамика” при выводе законов движения необходимо учитывать плотность и все физические свойства жидкостей. Учесть влияние всех этих параметров на условия движения жидкости невозможно, поэтому для облегчения решения задач гидродинамики введено понятие идеальной жидкости.

Идеальная жидкость – это условно принятая жидкость, не сжимаемая при изменении давления и не расширяющаяся при изменении температуры, обладающая абсолютной подвижностью, т. е. вязкость жидкости равна нулю; не сопротивляющаяся деформации разрыва.

Таким образом, законы и уравнения гидродинамики выводятся для идеальной жидкости, затем в них вносятся дополнительные члены, коэффициенты, поправки с учетом физических свойств и условий движения реальной жидкости.

потоки – это потоки жидкости, ограниченные твёрдыми поверхностями не со всех сторон и имеющие по всей длине свободную поверхность. Примерами таких потоков являются движение жидкости в реках, каналах, лотках, желобах и других открытых руслах.
4.3. Гидравлические элементы потока

Живое сечение (ω) – сечение струйки или потока плоскостью, нормальной в каждой своей точке к проходящей через неё линии тока. Другими словами, это сечение струйки или потока жидкости плоскостью, нормальной к направлению движения жидкости. Для равномерного и плавно изменяющегося движения живое сечение является плоским.

На рис. 4.2 представлено живое сечение для круглой трубы диаметром d, полностью заполненной жидкостью (рис. 4.2,а), и для открытого русла шириной b и глубиной наполнения h (рис. 4.2,б).

Смоченный периметр (χ) – длина контура живого сечения по твёрдым стенкам русла. На рис. 4.2,а для круглой трубы χ = πd = 2πr(длина окружности круглой трубы); для открытого потока (см. рис. 4.2,б) χ = 2h +b.

В гидродинамике поток жидкости рассматривается как совокупность элементарных струек (рис. 4.1,а).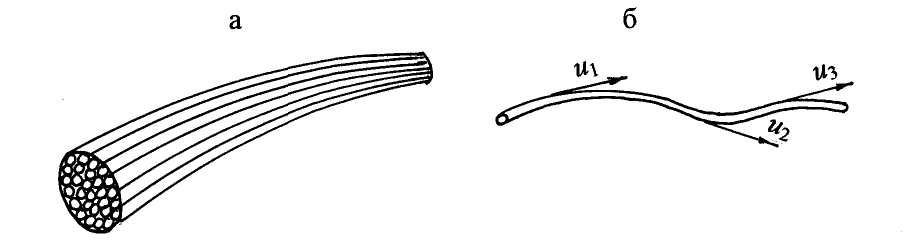



Рис. 4.1
Элементарная струйка – бесконечно малый замкнутый объём жидкости, поверхность которого образована линиями тока (рис. 4.1,б).

Линия тока – линия, в каждой точке которой в данное мгновение вектор скорости жидкости совпадает с касательной к этой линии.

Для элементарной струйки приняты свойства, которые используются в теоретических выводах:

а) форма струйки не изменяется с течением времени;

б) поверхность струйки непроницаема со стороны окружающей жидкости, жидкость не входит в струйку и не выходит из неё;

в) в силу малости нормального сечения струйки скорость в пределах сечения считается постоянной.

Различают два вида потоков: напорные и безнапорные потоки.

Напорные потоки – это потоки жидкости, ограниченные со всех сторон твёрдыми стенками. Движение происходит под действием разности давлений по длине потока. Разность давлений создаётся разностью уровней жидкости в резервуарах, водонапорной башней, насосом, вентилятором. Примерами служат движение воды, масла, нефти в трубопроводах, воздуха в вентиляционных системах и им подобных.

Гидравлический радиус (R) – отношение площади живого сечения к смоченному периметру: (4.1)

Для напорного потока в круглой трубе (см. рис. 4.2,а) гидравлический радиус

(4.2)

для открытого потока (см. рис. 4.2,б)

Безнапорные (открытые) потоки

а б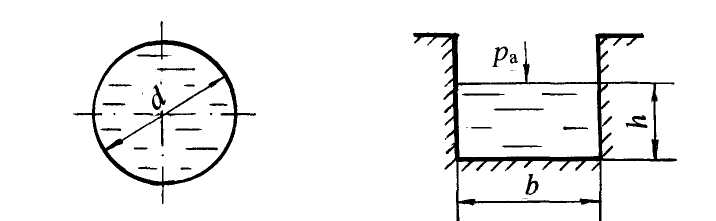


ω = πd²/ 4 = πr² ω = bh

Рис. 4.2


Гидравлический радиус R является универсальной геометрической характеристикой потока, которая может быть использована в теоретических выводах для потоков любой формы с различной степенью заполнения жидкостью.

4.4. Расход жидкости. Средняя скорость потока.

Уравнение неразрывности потока
Расходом называют количество жидкости, проходящее через живое сечение в единицу времени.

В зависимости от того, в чём выражают количество жидкости, различают: объёмный расход Q; массовый расход М; весовой расход G.

Для вывода расчётной формулы объёмного расхода рассмотрим элементарную струйку в установившемся движении, выделим в ней живое сечение dω, которое за время dtпереместится из положения 1 в положение 2, пройдя путь dl(рис. 4.3).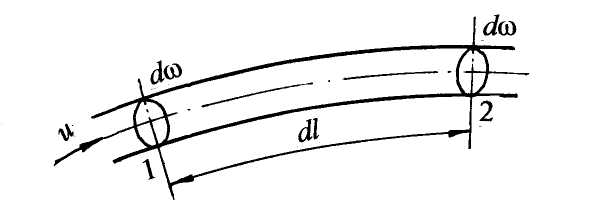



Рис. 4.3

Допустимо считать, что на расстоянии dl площадь живого сечения dω остаётся постоянной и скорость u в живом сечении также постоянна согласно свойствам элементарной струйки.

При перемещении живого сечения из положения 1 в положение 2 за время dt жидкость заполнит отсек 1-2 объёмом dW = dω·dl. Согласно определению, объёмный расход для элементарной струйки



При установившемся движении где u – скорость струйки в живом сечении. Объёмный расход для элементарной струйки:

dQ = udω.

Переходя к целому потоку жидкости, следует учесть, что скорости струек в пределах живого сечения потока изменяются по величине и по направлению. Чтобы найти расход жидкости для целого потока, следует просуммировать расходы струек по всему живому сечению, то есть проинтегрировать зависимость dQ по площади живого сечения потока ω:



Для инженерных расчётов вводится понятие средней скорости потока υ.

Средняя скорость – это такая одинаковая для всех струек скорость, при которой расход жидкости равен суммарному расходу элементарных струек с действительными скоростями.

Тогда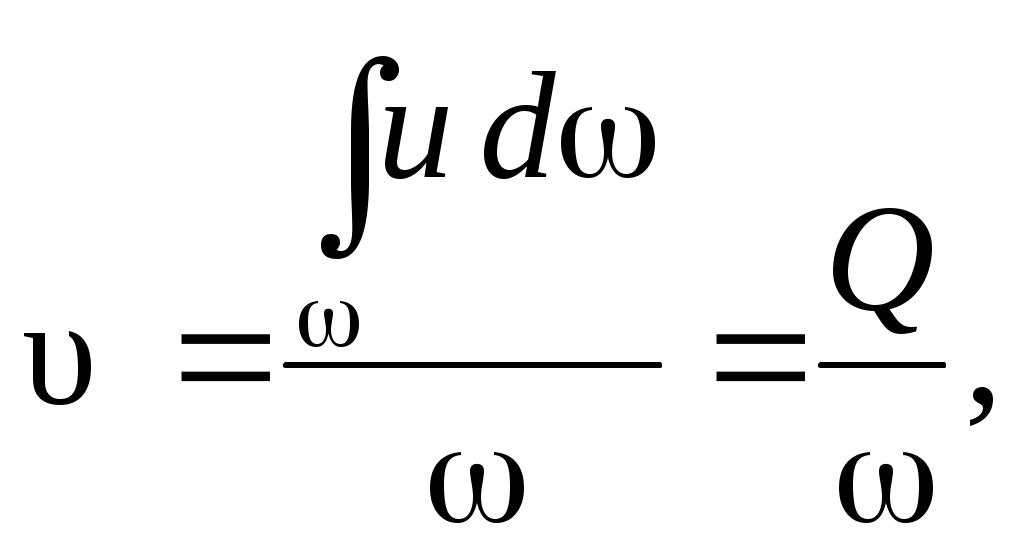

отсюда Q = υ ω. (4.3)
Единицы измерения: объёмного расхода Q, м³/с; (л/с); массового расхода M = ρQ, кг/с; весового расхода G = ρgQ, Н/с.

Экспериментальное определение объёмного расхода Q проводится объёмным методом, а именно фиксируется время наполнения t установленного объёма жидкости W в мерной ёмкости. Тогда

(4.4)

Объём протекающей жидкости W можно также определить по водомеру, счётчику воды или любому прибору для измерения скорости и расхода (примеры таких приборов будут рассмотрены ниже).

Важным уравнением в гидродинамике является уравнение неразрывности потока (приводится без вывода).

В случае если плотность жидкости величина постоянная (ρ = const), что имеет место при движении капельных жидкостей, уравнение неразрывности имеет вид: Q₁ = Q₂ = Q = const

или для двух сечений υ₁ ω₁ = υ₂ ω₂.

Как следствие можно записать

; (4.5)

для круглой трубы: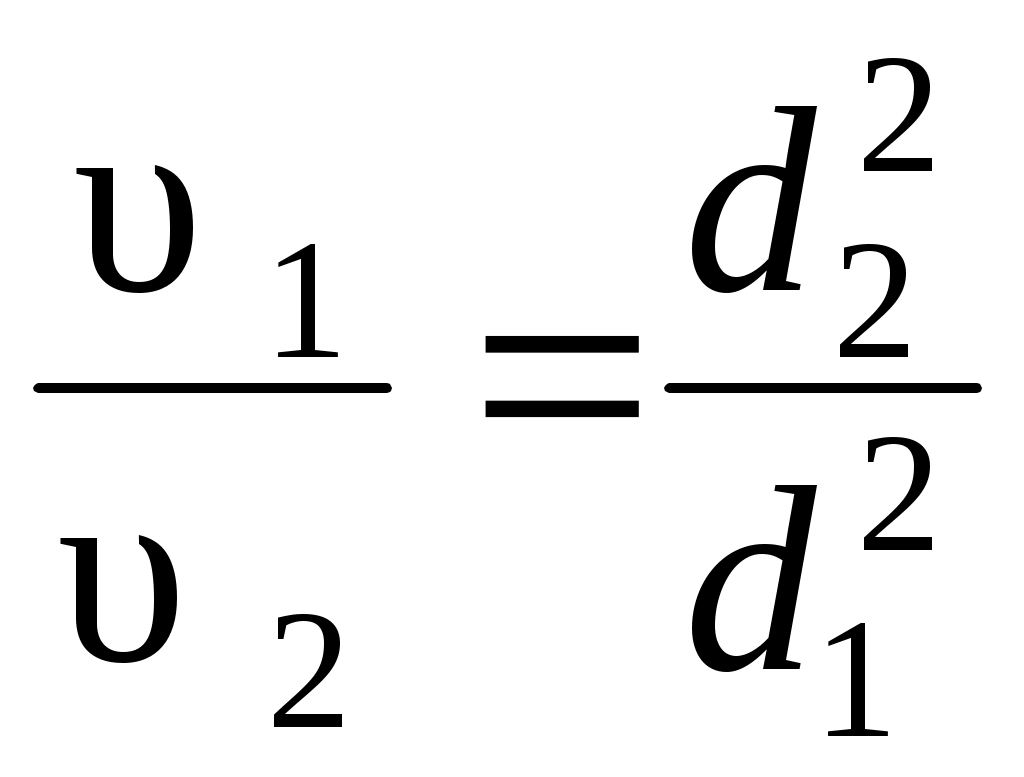

.

Для сплошного потока расход жидкости постоянный, скорости в живых сечениях обратно пропорциональны площадям живых сечений.
4.5. Основное уравнение гидродинамики.

Уравнение Д- Бернулли.
Уравнение Бернулли является основным уравнением гидромеханики. Принципы действия многих приборов, в том числе для измерения скорости и расхода жидкости, основаны на уравнении Бернулли.

В уравнении Бернулли установлена связь между основными параметрами движения: давлением, скоростью в живом сечении струйки или потока и геометрическим положением живого сечения струйки или потока жидкости. В данных лекциях рассматривается уравнение Бернулли для установившегося движения жидкости, находящейся в поле действия только сил тяжести.

Уравнение Бернулли выводится в три этапа:

1. 
   для элементарной струйки идеальной жидкости (см. понятия «идеальная жидкость» и «элементарная струйка» в разделе 4.2);
   
2. 
   для элементарной струйки реальной (вязкой) жидкости;
   
3. 
   для целого потока реальной жидкости.
   

4.5.1. Уравнение Бернулли для элементарной струйки идеальной жидкости

Идеальная жидкость – это условная жидкость, в которой отсутствует такое физическое свойство, как вязкость. Идеальная жидкость обладает абсолютной текучестью и движется без возникновения сопротивлений, поэтому энергия струйки остаётся постоянной по ходу движения.

Уравнение имеет вид: (4.6)

Для двух и более сечений по направлению движения струйки уравнение принимает вид:

(4.7)
4.5.2. Интерпретация уравнения Бернулли

Все члены уравнения имеют размерность длины, поэтому могут характеризоваться с геометрической точки зрения как высоты, или напоры, а с энергетической точки зрения как удельная энергия.
Геометрический смысл уравнения Бернулли:

z = h_геом – геометрическая высота, или геометрический напор, отсчитывается от произвольной горизонтальной плоскости сравнения;

= h_p– пьезометрический напор, или пьезометрическая высота (см. раздел 1.3). Пьезометрический напор соответствует показанию пьезометра в заданном сечении струйки;

= h_ск – скоростной напор в живом сечении струйки.

Уравнение (4.6) с геометрической точки зрения может быть записано:

h _геом + h_p +h _ск = H_полн = const, (4.8)

где Н_полн – полный напор в заданном сечении струйки.

Сумма геометрического и пьезометрического напоров называется статическим напором, обозначается Н _ст:

h _геом + h_p = H _ст или . (4.9)

Графическое представление уравнения Бернулли называется диаграммой уравнения.

Для построения первой диаграммы рассмотрим элементарную струйку идеальной жидкости в установившемся плавно изменяющемся движении.

По направлению движения струйки выделим в ней три живых сечения 1-1, 2-2, 3-3 с площадями живых сечений dω₁, dω₂, dω₃, со скоростями u₁, u₂, u₃ и давлениями в этих сечениях р₁,р₂, р₃ .

Представим графически уравнение (4.7).

Выбираем произвольно расположенную горизонтальную плоскость сравнения 0-0 (рис. 4.4). Отсчёты геометрических высот сечений z₁,z₂, z₃ от плоскости сравнения по вертикали вверх считаются положительными.

Откладываем z₁,z₂, z₃ для выделенных сечений по вертикали вверх.

В каждом сечении по вертикали следует прибавить пьезометрические напоры ,

затем скоростные напоры .

Поэтапно отложим эти напоры.

При построении диаграммы следует учесть, что для изображённой струйки (рис. 4.4) площадь второго живого сечения больше площади первого живого сечения, а площадь третьего живого сечения меньше площади первого живого сечения: dw₃ < dw₁ < dw₂.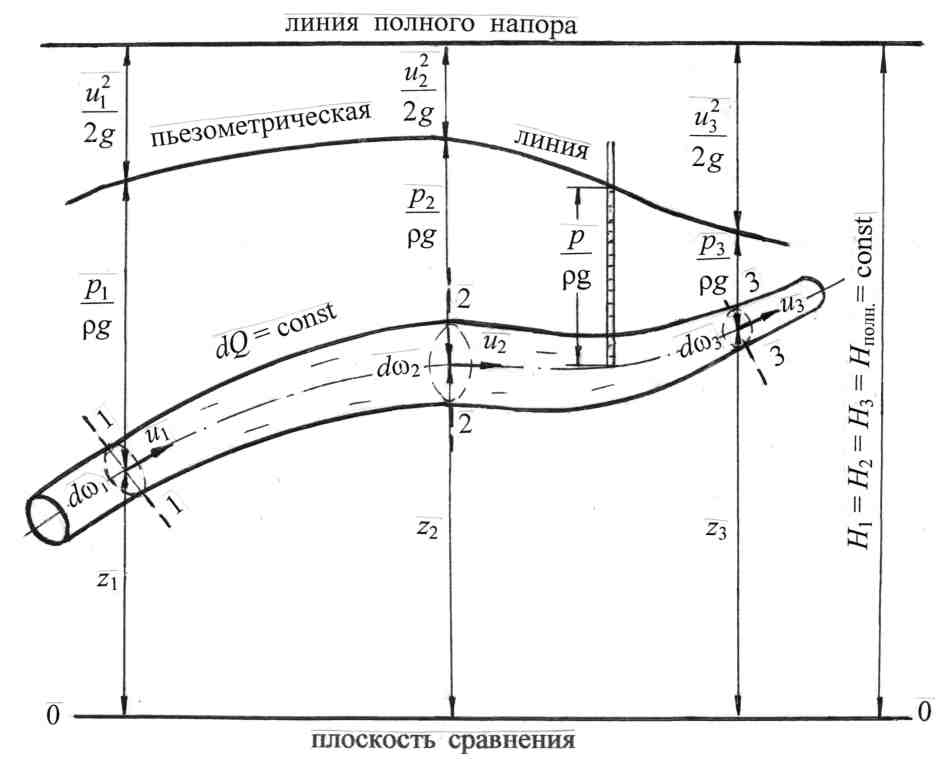


Рис. 4.4
При постоянном расходе жидкости элементарной струйки (dQ = const), согласно уравнению неразрывности (4.5), с уменьшением площади живого сечения скорость, а следовательно, и скоростной напор увеличиваются, при увеличении площади живого сечения скоростной напор уменьшается, значит:

.

В первом сечении к геометрическому напору z₁ по вертикали вверх прибавляем пьезометрический напор , затем скоростной напор .

Согласно формулам (4.7) и (4.8), полный напор во всех сечениях величина постоянная: Н₁ = Н₂ = Н₃ = Н_полн = const.

От суммы трёх напоров в первом сечении проводим горизонтальную линию. Для идеальной жидкости сумма трёх напоров во втором и в третьем сечениях располагается на том же горизонте, что и для первого сечения.

На рис. 4.4 обозначаем равенство полных напоров в сечениях и Н_полн = const.

Линия, соответствующая полному напору, называется линией полного напора.

Во втором сечении к геометрическому напору z₂ по вертикали вверх прибавляем пьезометрический напор и скоростной напор , причём < (увеличивается площадь живого сечения dw₂, значит, уменьшается скорость u₂ и скоростной напор ).

Таким образом, между первым и вторым сечениями скоростной напор уменьшается, а статический напор повышается.

В третьем сечении следует отложить скоростной напор > , затем пьезометрический напор . При увеличении скоростного напора статический напор уменьшается (см. рис. 4.4).

Линия, возвышающаяся на величину пьезометрического напора ( ) над осью струйки, называется пьезометрической линией.

Почему эта линия называется пьезометрической?

Воспользуемся понятиями «пьезометр» и «пьезометрическая высота». Пьезометр – это открытая вертикальная стеклянная трубка малого диаметра для измерения пьезометрического напора , выведенная от оси струйки (см. рис. 4.4). Поэтому можно сказать, что пьезометрическая линия проходит по горизонтам жидкости в пьезометрах, установленных вдоль оси струйки.

Анализ диаграммы показывает, что при постоянном расходе пьезометрическая линия может повышаться на участках увеличения площади живого сечения и понижаться при уменьшении площади живого сечения.

Энергетический смысл уравнения Бернулли

Все слагаемые уравнения представляют удельную энергию, т. е. отнесённую к единице веса:

z = е _полож – удельная потенциальная энергия положения;

= e_давл - удельная потенциальная энергия давления;

= e _кин – удельная кинетическая энергия.

С энергетической точки зрения уравнение Бернулли имеет вид:

е _полож + е _давл + е _кин = Е = const, (4.10)

где Е – полная удельная энергия струйки.

Для идеальной жидкости полная удельная энергия струйки остаётся постоянной для всех сечений по длине движущейся струйки. Таким образом, уравнение Бернулли выражает закон сохранения энергии.

Отдельные энергии вдоль движущейся струйки могут изменяться, но сумма их вдоль струйки идеальной жидкости должна быть неизменной.

При перемещении струйки от первого сечения ко второму скоростной напор во втором сечении ( ) уменьшается, следовательно, уменьшается удельная кинетическая энергия, значит, удельная потенциальная энергия повышается, действительно, величина ( ), соответствующая удельной потенциальной энергии, увеличивается. В третьем сечении скоростной напор ( ) увеличивается, значит, с энергетической точки зрения в третьем сечении увеличивается кинетическая энергия, а удельная потенциальная энергия в третьем сечении ( ) уменьшается (см. рис. 4.4).