гидравлика. !!ЛЕКЦ ЛАД ГИДР,2020. 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика

• Название: 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика
• Анкор: гидравлика
• Дата: 02.04.2021
• Размер: 1.61 Mb.
• Имя файла: !!ЛЕКЦ ЛАД ГИДР,2020.doc
• Тип: Документы; #190578
• страница: 2 из 9

1.4. Единицы измерения давления

Основной расчётной системой единиц измерения давления является система СИ. Но наряду с этой системой при технических расчётах и в производственной практике пользуются технической системой (CGS) и внесистемными единицами измерения.

Система СИ: 1 Н/м² = 1 Па; 10³ Па = 1 кПа; 10⁶ Па = 1 МПа; 1 бар = 10⁵ Па.

Техническая система: 1 ат = 1 кгс/см².

Внесистемные единицы измерения: мм рт. ст.; м вод. ст.; мм вод. ст.

Покажем перевод единиц измерения давления:

1 ат = 1 кгс/см² = 10⁴ кгс/м² = 9,8·10⁴ Н/м² = 98 кПа;

1 ат = 735,6 мм рт. ст.

1 ат = 10 м вод. ст.

1 мм рт. ст. = 133,3 Па.

Перевод единиц измерения давления из ат или Па в высоту столба жидкости и, наоборот, может быть выполнен по формулам:

Н = р/(ρg) и р = ρgH.

Проверим перевод единиц измерения давления. Переведём давление р = 1 ат = (98·10³) Па в м вод.ст., зная, что плотность воды ρ = 10³ кг/м³, ускорение свободного падения g = 9,8 м/с²:

Н_вод.ст. = (98·10³) / (10³·9,8) = 10 м.

Теперь переведём 1 ат в мм рт. ст. при плотности ртути ρ_рт.= 13,6·10³ кг/м³:

Н_рт.ст. = ( 98·10³ ) / ( 13,6·10³·9,8 ) = 0,7356 м = 735,6 мм.
2. Сила давления жидкости на плоские поверхности.
В практике гидравлических расчётов часто приходится определять величину и точку приложения силы давления жидкости на плоские стенки различной конфигурации. Такими плоскими стенками, воспринимающими давление жидкости, являются стенки резервуаров, плоские затворы, крышки, грани плотин, элементы гидротехнических сооружений и др.

Для определения силы давления жидкости на плоские стенки пользуются двумя методами - аналитическим и графо-аналитическим. Аналитический метод применяется для плоских поверхностей любой формы, графо-аналитический - только для прямоугольных поверхностей.
2.1. Аналитический метод определения силы давления жидкости

Для расчёта силы полного или абсолютного давления жидкости на плоскую поверхность пользуются аналитической расчётной зависимостью:

R_полн = р_C А. (2.1)

Сила полного давления жидкости на плоскую стенку равна произведению площади стенки (A) на полное давление на глубине погружения центра тяжести стенки в жидкость (р_C).

Согласно основномууравнениюгидростатики (1.1), давление на глубине погружения центра тяжести стенки:

р_C = р₀ + ρgh_C, (2.2)

где h_C – глубина погружения центра тяжести стенки в жидкость, отсчитанная от свободной поверхности;

ρ - плотность жидкости;

g - ускорение свободного падения.

В формуле (2.2) давление на поверхности жидкости р₀ может быть атмосферным, манометрическим (избыточным), вакуумметрическим. Формулу (2.1) с учётом формулы (2.2) можно записать:

R_полн = р₀A + ρgh_CA. (2.3)

Таким образом, сила полного давления может быть представлена в виде двух составляющих:

силы внешнего, илиповерхностного, давления:

R₀ = p₀A; (2.4)

силы весового давления жидкости:

R_ж =ρgh_С A. (2.5)

Сила полного давления R_полн находится как геометрическая сумма двух параллельных сил R₀ и R_ж:



Давление на поверхности жидкости, согласно закону Паскаля, передаётся внутрь жидкости всем точкам без изменения. Это значит, что эпюра внешнего давления p₀ представляет равномерно распределённую прямоугольную нагрузку, а равнодействующая такой нагрузки R₀ приложена в центре тяжести поверхности стенки, т. е. на глубине h_С .

Составляющая от весового давления жидкости R_ж приложена в точке, называемой центромдавления.

Центр давления силы R_ж располагается ниже центра тяжести стенки. Глубина погружения центра давления h_D рассчитывается по формуле:

(2.6)

,

где: – эксцентриситет центра давления, его величина соответствует смещению центра давления относительно центра тяжести;

I_C – центральный момент инерции плоской стенки относительно горизонтальной оси, проходящей через центр тяжести С.

α– угол наклона плоской стенки к горизонту.

В табл. 3 для некоторых плоских симметричных фигур приведены формулы для определения центральных моментов инерции относительно горизонтальной оси, площадей и координат их центров тяжести.

Для определения точки приложения силы полного давления R_полн нужно воспользоваться теоремой о моменте равнодействующей: момент равнодействующей относительно какой-либо оси равен сумме моментов, её составляющих, относительно той же оси.
2.2. Графо-аналитический метод расчёта силы давления

и центра давления на прямоугольные поверхности

Графо-аналитический метод расчёта силы давления основан на построении эпюр гидростатического давления.

Эпюры давления представляют собой неравномерно распределённую нагрузку по ширине (или длине) плоской прямоугольной поверхности.

Определим силу давления жидкости на прямоугольную стенку АВ высотой Н и длиной l, перпендикулярной плоскости чертежа. Удерживаемый напор равен высоте стенки (рис. 2.1). Совместим прямоугольную стенку с плоскостью чертежа и покажем положение центра тяжести стенки точку С.

Рассчитаем силу давления жидкости R_ж аналитически и графически.
Аналитический метод расчёта.

Согласно формуле (2.5), сила давления жидкости

, (2.7)

где h_C = H/2; A=Hl.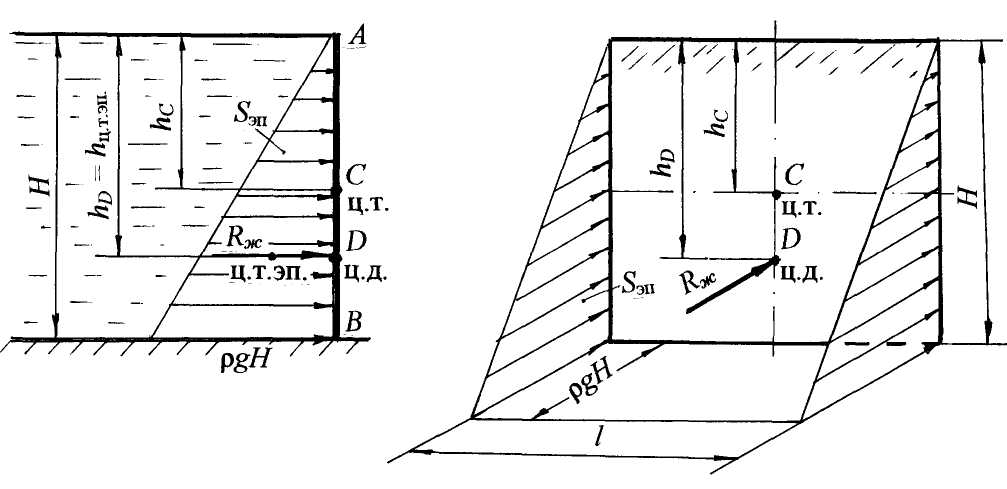



Рис. 2.1
Положение центра давления рассчитываем по формуле (2.6):



где центральный момент инерции относительно горизонтальной оси для прямоугольника (см. приложение, табл. 3); α = 90⁰; sin α = 1,0.

Таким образом, (2.8)

Рассмотрим графо-аналитический метод расчёта силы давления и центра давления. Построим эпюру гидростатического давления. Давление жидкости в точке А р_А=0, в точке В - р_В =ρgH.

Эпюра давления в плоскости чертежа представляет треугольную нагрузку, в объёмном представлении – это треугольная призма. Равнодействующая такой нагрузки равна объёму треугольной призмы и проходит через центр тяжести этой призмы. В плоскости чертежа сила давления жидкости R_ж проходит через центр тяжести эпюры гидростатического давления.

Проверим: (2.9)

где S_эп – площадь эпюры давления в виде треугольника.

Центр тяжести эпюры гидростатического давления располагается на расстоянии 2/3 Н (центр тяжести треугольника):

h_ц.т.эп = 2/3 H. (2.10)

Сравнивая формулы (2.7) и (2.9), а также (2.8) и (2.10), приходим к выводу: графо-аналитически сила давления жидкости на прямоугольные поверхности равна произведению площади эпюры гидростатического давления на длину (или ширину) плоской стенки и проходит через центр тяжести эпюры давления:

R_ж = S_эпl; h_D = h_ц.т.эп. (2.11)
3. Сила давления жидкости на криволинейные поверхности

3.1. Основные понятия и теоретические положения

Примерами криволинейных поверхностей, испытывающих давление покоящейся жидкости, являются сферические и цилиндрические стенки резервуаров, секторные, сферические и цилиндрические затворы, клапаны насосов, поверхности трубопроводов и т. п.

В практике инженерных расчётов ставятся задачи определения силы давления на криволинейные поверхности, необходимых усилий для открытия клапанов и затворов или удержания их в закрытом положении.

Для упрощения расчетов принято считать, что равнодействующая давления на криволинейную поверхность определяется как геометрическая сумма составляющих по двум или трём выбранным направлениям:

. (3.1)

Чаще всего криволинейные поверхности, используемые в технике, имеют ось симметрии или ось вращения. Для таких поверхностей при определении силы давления жидкости достаточно двух составляющих - горизонтальной и вертикальной:

(3.2)

Горизонтальная составляющая силы давления на криволинейную поверхность равна силе давления жидкости на плоскую вертикальную проекцию криволинейной поверхности:

R_x = ρgy_CA_y , (3.3)

где ρ – плотность жидкости;

A_y – площадь вертикальной проекции криволинейной поверхности;

y_C - координата центра тяжести вертикальной проекции, отсчитанная от свободной поверхности.

Глубина погружения центра тяжести вертикальной проекции h_C совпадает с координатой центра тяжести y_C , поэтому в дальнейшем y_Cможно называть глубиной погружения центра тяжести или напором на уровне центра тяжести вертикальной проекции криволинейной поверхности.

Другими словами, чтобы найти горизонтальную составляющую силы давления жидкости, нужно криволинейную поверхность спроектировать в жидкость на вертикальную плоскость и найти силу давления на полученную проекцию.

Сравнивая формулу (3.3) с формулой силы давления жидкости на плоскую стенку (2.5), видим аналогию расчётных зависимостей.

Координату y_Dили глубину погружения точки приложения горизонтальной составляющей, т. е. центра давления, определяем по формуле для вертикальной плоской поверхности:

(3.4)

где I_C– центральный момент инерции вертикальной проекции относительно горизонтальной оси.

Вертикальная составляющая силы давления на криволинейную поверхность равна силе тяжести жидкости в объёме “ тела давления”:

R_y = ρgV_т.д , (3.5)

где V_т.д – объём тела давления.

Рассмотрим понятие “ тело давления”.

Тело давления – это криволинейный объём, ограниченный:

а) самой криволинейной поверхностью;

б) поверхностью, образованной вертикальными проектирующими линиями, проведёнными из контура криволинейной поверхности до свободной поверхности или её продолжения;

в) горизонтальной проекцией криволинейной поверхности насвободнуюповерхностьжидкости или её продолжение.

Различают два вида тела давления.

1) Реальное, действительное или положительное тело давления.

Это случай, когда тело давления построено на смоченной части криволинейной поверхности, заполнено жидкостью, т. е. сила тяжести жидкости реально действует на криволинейную поверхность. Вертикальная составляющая силы давления R_y из центра тяжести объёма тела давления направлена вниз и также считается положительной.

Примеры положительного тела давления и вертикальной составляющей для криволинейной поверхности АВпредставлены на рис. 3.1.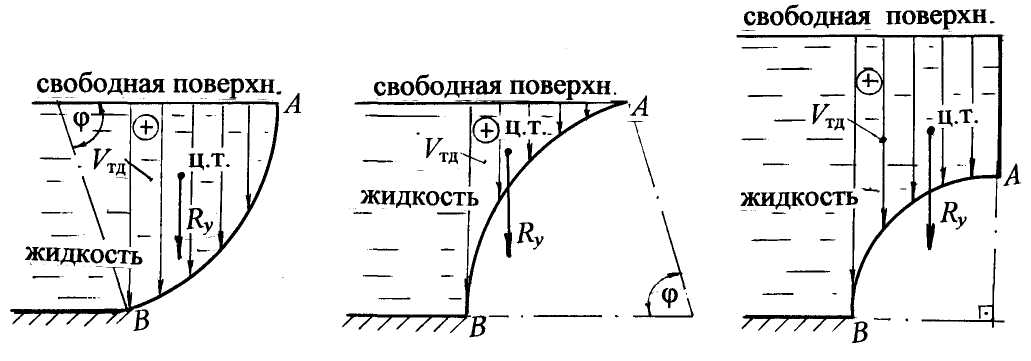






Рис. 3.1
2) Фиктивное, мнимое или отрицательное тело давления.

Это случай, когда тело давления построено на сухой части криволинейной поверхности. Жидкость в объёме тела давления отсутствует. Вертикальная составляющая R_y, из центра тяжести объёма тела давления направленная вверх, считается отрицательной.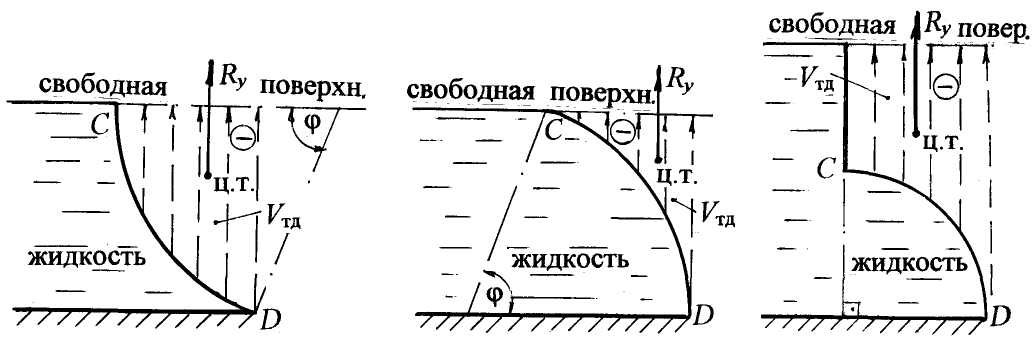


Рис. 3.2

Примеры отрицательного тела давления и вертикальной составляющей для криволинейной поверхности CD приведены на рис. 3.2.

Чтобы определить объём тела давления и его вид (положительное или отрицательное), нужно из контура криволинейной поверхности, т. е. из всех точек криволинейной поверхности, провести вертикальные линии до свободнойповерхности жидкости или её продолжения.

Если очерченный вертикальными линиями объём заполнен жидкостью, тело давления построено на смоченной части криволинейной поверхности, оно считается положительным. Стрелками, направленными вниз, показываем, что жидкость давит на криволинейную поверхность (см. рис. 3.1).

Таким образом, выделенный объём можно назвать эпюройтеладавления. Определяем положение центра тяжести тела давления. Из центра тяжести объёма вертикальную составляющую R_y направляем вниз.

В противном случае, если очерченный вертикальными линиями объём тела давления построен на несмоченной поверхности и не заполнен жидкостью, тело давления считается отрицательным. Стрелками, направленными вверх, показываем, что жидкость как бы вытеснена за счёт конфигурации криволинейной поверхности. Из центра тяжести отрицательного тела давления вертикальная составляющая R_y направлена также вверх (см. рис. 3.2).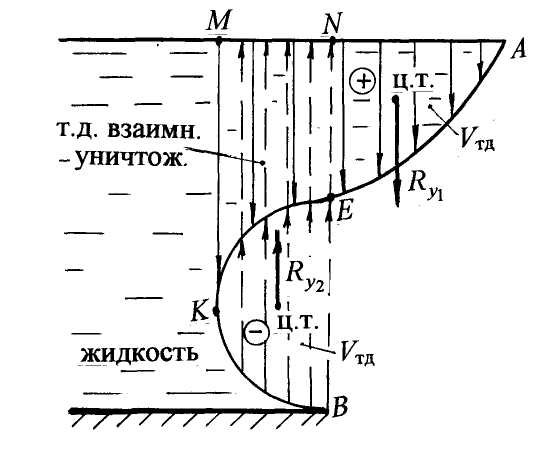

Рис. 3.3

Рассмотрим случай, когда при построении может получиться не одно, а два тела давления (рис. 3.3).

Имеем криволинейную поверхность АКВ, удерживающую некоторый напор жидкости. Криволинейную поверхность можно разделить на две части - АКи КВ. Для части АК строим тело давления по приведённой методике. Получаем положительное тело давления объёмом АКМА, построенное на смоченной стороне АК.

Для части криволинейной поверхности КВ тело давления объёмом КВNМК построено на несмоченной стороне КВ - отрицательное.

В объёме КМNEК происходит наложение отрицательного тела давления на положительное, два тела давления взаимно уничтожаются (компенсируются, сокращаются).

После построений имеем два тела давления: положительное объёмом ANEА, сила из центра тяжести тела давления направлена вниз; отрицательное объёмом ЕКВЕ, сила направлена вверх.

В приведённых примерах “тела давления“ эпюру положительного тела давления заштриховываем сплошными линиями, отрицательного – пунктирными. Такую же штриховку будем показывать в приведённых примерах и задачах.