гидравлика. !!ЛЕКЦ ЛАД ГИДР,2020. 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика

• Название: 16 1, с. 6 20. 03. 02. Природообустройство и водопользование. Гидравлика
• Анкор: гидравлика
• Дата: 02.04.2021
• Размер: 1.61 Mb.
• Имя файла: !!ЛЕКЦ ЛАД ГИДР,2020.doc
• Тип: Документы; #190578
• страница: 5 из 9

Гидравлические сопротивления.

5.1. Потери напора в гидравлических сопротивлениях.
Дополнительный член уравнения Бернулли h_w (см. формулу (4.15)) соответствует потерям напора в гидравлических сопротивлениях, которые складываются из суммарных потерь напора в местных сопротивлениях Σh_r и потерь напора по длине h_l:

h_w = Σh_r +h_l . (5.1)
В гидродинамике принято считать, что потери напора в любом гидравлическом сопротивлении пропорциональны скоростному напору

.

Местными сопротивлениями называются различного рода устройства, при прохождении через которые происходит деформация потока, изменение направления движения жидкости или величины скорости, или того и другого.

К местным сопротивлениям относятся краны, задвижки, отводы (колена), внезапное сужение, внезапное расширение, вход в трубу и прочие.

Знак суммы Σ в местных сопротивлениях показывает, что на одном трубопроводе может быть установлено несколько местных сопротивлений, потери напора в которых суммируются.

Теоретически потери напора в местном сопротивлении рассчитываются по формуле Вейсбаха : , (5.2)

где ζ – коэффициент местного сопротивления, значения которого, как правило, устанавливаются экспериментально, для некоторых видов местных сопротивлений коэффициент ζ рассчитан теоретически. На величину коэффициента ζ влияют геометрические размеры, конфигурация местного сопротивления и режим течения жидкости.

Потери напора по длине – это потери напора, возникающие при движении жидкости вдоль стенок трубопровода, зависящие от диаметра d, длины трубы l, скоростного напора и состояния внутренней поверхности трубы. Потери напора по длине называются также линейными потерями и рассчитываются по формуле Дарси-Вейсбаха:

, (5.3)

где λ – коэффициент гидравлического сопротивления, или коэффициент Дарси.

Значение коэффициента λ или выбор расчётной зависимости этого коэффициента зависит от режима движения жидкости и шероховатости трубы (или другого русла).

В гидродинамике введено понятие единичных, или удельных, потерь напора по длине, называемых гидравлическим уклоном: I = h_l/l.

С учётом формулы (5.3) гидравлический уклон рассчитывается по формуле:

. (5.4)

Результаты исследований показали, что гидравлический уклон является функцией скорости I=f(υ), её можно представить в виде I=aυⁿ, где коэффициент aи показатель степени n зависят от режима движения жидкости и состояния внутренней поверхности трубы или иного русла, т. е. их шероховатости. Иногда при расчётах потери напора в местных сопротивлениях заменяют потерями напора в прямолинейном участке трубы эквивалентной длины.

Эквивалентная длина l_э– это такая длина прямолинейного участка трубы, потери напора в котором равны (эквивалентны) потерям напора в местном сопротивлении при том же расходе жидкости:

, (5.5)

значит, . (5.6)

5.2. Потери напора по длине

при ламинарном режиме движения жидкости
Исследования Рейнольдса и других учёных показали, что при ламинарном режиме потери напора пропорциональны скорости в первой степени и зависят только от числа Рейнольдса Re.

Аналитически выведена формула для гидравлического уклона (вывод этой зависимости приведён во всех учебниках и учебных пособиях) при ламинарном режиме:

. (5.7)

Сравнив формулу (5.7) с формулой (5.4), заключаем, что при ламинарном режиме коэффициент гидравлического сопротивления λ:

, т. е. λ = f (Re). (5.8)

Потери напора по длине при ламинарном режиме соответственно рассчитываются по формуле Пуазейля:

, (5.9)

При подстановке формулы (4.20) для критерия Рейнольдса в формулы (5.7) и (5.9) заключаем, что при ламинарном режиме гидравлический уклон I и потери напора по длине h_l пропорциональны скорости в первой степени.

Формула (5.9) носит имя автора доктора медицины Пуазейля, который исследовал движение жидкости, в частности крови, в капиллярных трубках, вывел эту формулу эмпирически; в гидродинамике формула доказана аналитически.
5.3. Потери напора по длине при турбулентном режиме

Турбулентное течение жидкости является наиболее распространённым в технике, но представляет в то же время одно из сложных гидравлических процессов. Многочисленные исследования учёных показали, что создать строгую теорию турбулентного режима не представляется возможным, поэтому для теоретических и инженерных расчётов пользуются экспериментальными данными, графическими зависимостями и эмпирическими формулами.

Как отмечено выше, при числах Рейнольдса Re<Re_кр имеет место ламинарный режим движения.

С возрастанием скорости потока и чисел Рейнольдса снижается устойчивость ламинарного режима, начинаются колебательные движения струек, появляются пульсации скорости, т. е. кроме продольных составляющих скорости возникают поперечные составляющие, при дальнейшем увеличении скорости образуются завихрения, неупорядоченное движение, перемешивание потока, т. е. режим движения становится турбулентным.

Разрушение ламинарного течения начинается с оси потока, постепенно образуется турбулентное ядро потока, а у стенки трубы остаётся пограничный (пристеночный) слой, который состоит из ламинарного (вязкого) подслоя и переходного слоя.

Ламинарный подслой расположен непосредственно у стенки трубы, скорость в нём меняется от 0 у стенки (частицы жидкости просто прилипают к стенке и не двигаются) до некоторой величины. Изменение скорости в пределах вязкого слоя близко к линейному закону.

Толщина ламинарного подслоя δ имеет малую величину (от долей миллиметра до 1-2 мм) и рассчитывается по формуле: . (5.10)

Из формулы (5.10) следует, что с увеличением числа Рейнольдса Re толщина вязкого подслоя уменьшается.

5.3.1. Понятие о гидравлически гладких и шероховатых трубах

Рассмотрим, как влияет шероховатость труб на потери напора по длине при турбулентном режиме.

На внутренней поверхности трубы имеются неровности, выступы, которые называются шероховатостью.

Различают:

а) абсолютную шероховатость, которая соответствует высоте выступов, неровностей, обозначается Δ, измеряется в мм;

б) относительную шероховатость: или ;

в) относительную гладкость – величину, обратную относительной шероховатости: или .

Форма и высота выступов и неровностей вдоль стенки трубы неодинаковы, поэтому измерить и учесть абсолютную шероховатость практически невозможно. С целью упрощения гидравлических расчётов введено понятие эквивалентной шероховатости Δ_э, при которой потери напора в трубе равны (эквивалентны) потерям напора с фактической неоднородной шероховатостью.

В данных лекциях в расчётных формулах эквивалентная шероховатость Δ_э упрощённо может записываться как абсолютная шероховатость Δ.

Значение эквивалентной шероховатости Δ_э для некоторых видов труб приведено в табличных данных.

При турбулентном режиме можно выделить три зоны (области) сопротивления.

1. Движение вдоль гладких стенок. Это случай, когда толщина вязкого слоя больше абсолютной шероховатости (δ>Δ_э). Турбулентное ядро скользит по ламинарному подслою. Выступы, неровности перекрыты вязким слоем, шероховатость не влияет на потери напора.

Такие трубы называют “гидравлически гладкими”. Потери напора по длине пропорциональны скорости υ^1,75. Коэффициент гидравлического сопротивления λ не зависит от шероховатости и является функцией только числа Рейнольдса Re.

Для этой зоны сопротивления пользуются эмпирической формулой Блазиуса:

, т. е. λ = f (Re). (5.11)

2. Зона доквадратичного сопротивления. Это область сопротивления, в которой потери напора зависят как от числа Рейнольдса Re, так и от шероховатости. Потери напора по длине пропорциональны скорости υ^1,75-:-2,0, т. е. степенной коэффициент скорости n < 2,0, отсюда и название – “зона доквадратичного сопротивления”.

В этой области происходит переход от гидравлически гладкого к вполне шероховатому трению.

А. Д. Альтшуль обобщил экспериментальные данные, графические зависимости и теоретические положения ряда учёных и для зоны доквадратичного сопротивления предложил эмпирическую формулу

, т. е. λ = f (Re ; ). (5.12)

3. Зона квадратичного сопротивления. Это движение, при котором толщина вязкого слоя меньше абсолютной шероховатости (δ<Δ_э). Вязкий слой при больших числах Рейнольдса Re практически разрушен, турбулентное ядро касается неровностей, возникают дополнительные завихрения и связанные с ними потери напора. Потери напора по длине пропорциональны скорости υ², отсюда и название – “зона квадратичного сопротивления”.

Коэффициент гидравлического сопротивления λ является функцией шероховатости. Другое название этой области сопротивления – “движение вдоль шероховатых стенок”, а трубы называют “гидравлически шероховатыми”.

Для этой области в соответствии с гидравлическими особенностями явлений турбулизации применимы эмпирические формулы многих учёных. Для практических расчётов рекомендуется пользоваться формулами:

формула Никурадзе: 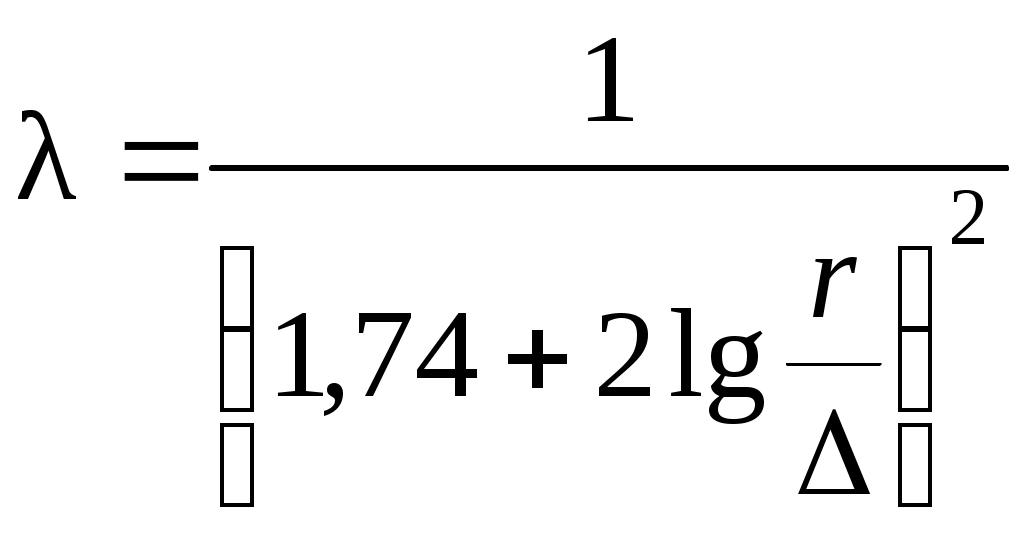, т. е. λ = f (5.13)

формула Шифринсона: т. е. λ = f (5.14)

Для турбулентного режима формула А. Д. Альтшуля (5.12) признана наиболее обобщённой и удобной для практических расчётов, так как вычисления по ней сводятся к элементарным алгебраическим действиям и дают надёжные результаты.

Согласно теории Альтшуля при 2300< Re< 20 второе слагаемое в формуле (5.12) значительно меньше первого, на потери напора влияет только число Рейнольдса Re, и формула практически совпадает с формулой Блазиуса (5.11): ; λ = f( Re). (5.15)

Как правило, эта зона сопротивления соответствует числам Рейнольдса до Re = 2·10⁴.

При числах Рейнольдса 20 < Re< 500 на потери напора оказывают влияние как число Re, так и относительная шероховатость , имеет место зона доквадратичного сопротивления.

Коэффициент гидравлического сопротивления λ следует рассчитывать по формуле (5.12): .

Границы изменения чисел Рейнольдса Re = 2·10⁴ - 5·10⁴.

При числах Рейнольдса Re > 500 имеет место зона квадратичного сопротивления, или движение вдоль шероховатых стенок. В формуле (5.12) первое слагаемое значительно меньше второго, им можно пренебречь. Потери напора по длине зависят только от относительной шероховатости , и формула (5.12) переходит в формулу (5.14) .

Согласно графической зависимости А. Д. Альтшуля, для этой области сопротивления значения чисел Рейнольдса находятся в пределах Re= 5·10⁴ - 10⁶.

Из вышеизложенного следует, что понятия “гидравлически гладкие” и “гидравлически шероховатые“ трубы относительны. Так, одна и та же труба с определённой шероховатостью может считаться гидравлически гладкой или шероховатой в зависимости от скорости движения (или числа Re), тогда для коэффициента гидравлического сопротивления λ выбирается соответствующая расчётная формула.

5.3.2. Потери напора по длине

в трубах с описательной шероховатостью

В гидравлических расчётах трубопроводов и других русел часто приходится встречаться с такой внутренней поверхностью трубы (бетонные, асбестовые, загрязнённые, водосточные трубы и им подобные) или иного русла (канала, лотка, жёлоба), для которых даётся описание состояния внутренней поверхности трубы, т.к. невозможно определить абсолютную шероховатость. В этом случае предложено коэффициент гидравлического сопротивления λ рассчитывать по формуле Шези: , (5.16)

где С – коэффициент Шези.

Коэффициент Шези С зависит от многих факторов, в том числе от геометрических размеров и состояния внутренней поверхности трубы или другого русла. Наиболее простой формулой для определения коэффициента Шези является формула Маннинга: , (5.17)

гдеnили 1/n – коэффициенты шероховатости стенок трубы или русла по описанию, приводятся в таблицах; R – гидравлический радиус, м. (согласно формуле (4.2), для круглой трубы гидравлический радиус R =d/4).
5.3.3. Потери напора по длине,

выраженные через обобщённые параметры.
В практике расчётов гидравлических систем, в частности трубопроводных систем, часто приходится рассчитывать потери напора по длине не через скорость υ, а через расход Q, который известен или его нужно определить.

Преобразуем формулу (5.3) потерь по длине: .

а) выразим скорость через расход: ;

б) введём гидравлический радиус: d = 4R;

в) коэффициент гидравлического сопротивления λ запишем по формуле (5.16): .

Получим: . (5.18)

В формуле (5.18) обозначим С²ω²R = K²,

где называется модулем расхода, или расходной характерис-тикой, единица измерения м³/с. Формула (5.18) принимает вид:

. (5.19)

Для удобства практических расчётов величина 1/K² обозначается через А: , (5.20)

где А– удельное сопротивление (сопротивление единицы длины), единица измерения с²/м⁶.

Таким образом, потери напора по длине рассчитываются по формуле

. (5.21)

В приведённых формулах параметры К и А называют обобщёнными параметрами, значения которых приводятся в таблицах (см. приложение, табл. 8) для нормальных водопроводных труб, другое название – водопроводные трубы в нормальных условиях.