Лекции по теплопередачи (Конвективный теплообмен, Word). 2. конвективный теплообмен основные понятия и определения

• Название: 2. конвективный теплообмен основные понятия и определения
• Дата: 04.11.2022
• Размер: 1.22 Mb.
• Имя файла: Лекции по теплопередачи (Конвективный теплообмен, Word).doc
• Тип: Документы; #770565
• страница: 7 из 7

2.8 Теплоотдача при свободном движении жидкостей и газов.

Свободным движением называется движение жидкости или газа, возникающее вследствие разности плотностей нагретых и холодных частей жидкости под давлением гравитационных сил. Такое движение еще называют естественной конвекцией.

Процесс теплообмена при свободном движении жидкости имеет широкое распространение в природе, быту и технике. В быту это например нагрев помещений от печей и батарей, утренний и вечерний бриз на море, в технике - нагревание воды в котлах, остывание поверхностей машин и аппаратов, частично при вынужденном движении жидкости и т. д.

По характеру протекающих процессов при свободной конвекции все их можно разбить на 2 больших случая: свободная конвекция в неограниченном объёме и свободная конвекция каналов. Начнем с первой из них.
2 .8.1 Свободная конвекция в неограниченном объёме
Сразу оговоримся, что мы будем понимать под неограниченным объемом. Под неограниченным объемом мы будем понимать объем (наша комната), размеры которого настолько велики, что тепловое возмущение, вносимое находящейся в нем нагретым телом, не распространяется на весь объем, в связи с чем на некотором удалении от тела жидкость можно считать не возмущенной. Вот такой объем мы и рассмотрим.


Пусть в такой не ограниченный объем мы с вами внесли трубу с температурой стенки t_с>t_ж. В этом случае между средой и телом будет наблюдаться теплообмен холодных и горячих частиц жидкости, под действие гравитационных сил возникнет свободная конвекция.

Частицы жидкости, соприкасающиеся с поверхностью нашей трубы будут нагреваться и как более легкие подниматься в верх, так как более холодные и соответственно более плотные частицы жидкости будут их вытеснять и занять место у горячей стенке. На лицо свободной конвекции, которая всецело определяется наличием теплообмена.

Возникающее при этом подъемная сила определяется как:

p=g(ρ₀-ρ) н/м³ (p=gρ₀-gρ), (*)

где ρ_o и ρ- плотности жидкости в 2 – х точках с разной температурой.

g- ускорение свободного падения.

Эту подъемную силу можно выразить через коэффициент объемного расширения жидкости β и разность температур в объеме жидкостей ∆t=t_c-t_ж(у стенки температура частиц жидкости равнаt_c , а на удалении t_ж - температуре жидкости в объеме).

Мы с вами говорим, что коэффициент объемного расширения β характеризует изменение объема жидкости при её нагревании на 1 К и выражается как . Величины плотности и удаленного объема взаимосвязаны, т.е. ρ=1/ν. Исходя из этого определения коэффициента объемного расширения его можно выразить через плотность.

; ;

ρ=βρ∆t+ρ

Полученное выражение подставим в (*) и получим

P=gβρ∆t

Мы можем сделать вывод, что подъемная сила при свободном движении зависит от физических свойств жидкостей (β;ρ) и разности температур в объеме жидкости ∆t=t_c-t_ж. Так как интенсивность свободного движения определяться величиной подъемной силой P, то следовательно режим его будет определяться теме же факторами (β;ρ и ∆t). Отметим, что наибольшее влияние на режим движения (ламинарный или турбулентный) оказывает температурный напор ∆t. При малом температурном напоре наблюдается ламинарный режим, а при большом – турбулентный.

Однако, на начальном участке теплообмена (как в нашем примере) движение, не смотря на большой ∆t будет всегда ламинарным. Это участок тепловой и гидромеханической стабильности.

В нижней части поверхности (см. рис. на предыдущей странице) в месте зарождения свободного движения. Жидкость движется ламинарно, при этом толщина ламинарного пограничного слоя растет в направлении движения. Рост толщины ламинарного пограничного слоя приводит к уменьшению значения α от max на входе до min на некотором удалении от начала поверхности х_кр. Здесь начинается разрушение ламинарного пограничного слоя и переход его в турбулентный. Коэффициент теплоотдачи α увеличивается и принимает постоянное значение для данного режима движения.

Таким образом можно сделать вывод:

Характер и развитие свободного движения в неограниченном объеме жидкости полностью определяется теплообменом. Чем больше ∆t и F, тем, в соответствии с формулой Ньютона – Рихмана Q=αF∆t, больше тепловой поток от стенки к жидкости (и более интенсивное движение жидкости).

Коэффициент теплоотдачи α будет в основном зависеть от температурного напора ∆t, физических свойств жидкости Pr и кроме того от размера (площади F) и расположения поверхности.

Рассмотренная нами картина свободного движения вдоль вертикальной трубы характерна так же для вертикальной стенке, наклонных и горизонтальных труб круглого и овального сечения. Это объясняется тем, что в развитии свободного движения форма тела играет второстепенную роль, главное это протяженность поверхности, вдоль которой идет движение нагретого газа.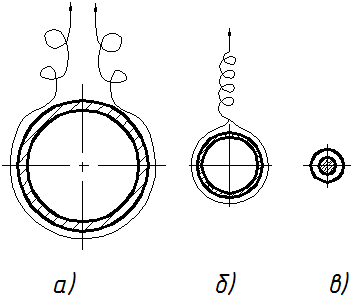



Чем больше диаметр трубы, тем раньше происходит разрушение ламинарного пограничного слоя. Для труб малого диаметра оно может происходить вдали от трубы (рис. б). у них F мала, количество передаваемого тепла незначительно и ламинарный режим течения сохраняется и при больших∆t.

Для тонких проволочек (d=0,2…1мм) при малых температурных напорах вокруг проволочки образуется почти не подвижная пленка нагретого воздуха (большое термическое сопротивление (λ мала)). Такой режим называется пленочным.

Несколько иная картина наблюдается при движении среды около горизонтальных плоских стенок или плит. Оно сильно зависит от их положения и размеров.


Для небольшой нагретой поверхности обращенной вверх движения идет по схеме (а), жидкость ламинарно движется вдоль поверхности на некотором расстоянии от неё переходит к турбулентному режиму движения.

Если плитка имеет большие размеры то вследствие наличия с краев сплошного потока нагретой жидкости центральная часть плиты оказывается изолированной. Её вентиляция происходит лишь за счет притока (провала) холодной жидкости сверху (б).

Если же поверхность обращена вниз, то движение происходит лишь в тонком слое под поверхностью (в). Основная масса жидкости ниже этого слоя остается неподвижной.

В литературе вы можете найти обширный экспериментальный материал касающийся вопросов свободного движения жидкости. Все они как правило представлены в виде графиков (М.А. Михеев, Основы теплопередачи стр. 72-73) . Все эти данные на основе теории подобия представляются в виде степенной функции вида:

(1)

В отличие от уравнений вынужденного движения жидкости мы видим, что у нас отсутствует число и появляется число Gr.

- оно характеризует возникающую в жидкости подъемную силу за счет разности температур ∆t

- характеризует физические свойства рассматриваемой жидкости.

Присутствующий в уравнении комплекс (Gr_ж;Pr_ж) как раз и определяет режим свободного течения жидкости (ламинарный или турбулентный) так же как его определяет число Re для вынужденного движения. Этот комплекс называется числом Релея.

Gr_ж;Pr_ж =Ra_ж - определяет режим движения.

При (Gr_ж;Pr_ж)<1, Nu_ж=0,5 и остается постоянной, поэтому α_ж=0,5(λ_ж/d) т.е. теплоотдача полностью определяется теплопроводностью среды. Это соответствует пленочному режиму. Однако пленочный режим весьма не устойчив и уже при Ra=10^-3 может переходить в ламинарный.

При 10³<(Gr_ж;Pr_ж)<10⁹ устанавливается основной ламинарный режим, а при (Gr_ж;Pr_ж)>6∙10¹⁰ - основной турбулентный. В промежутках наблюдается переходный режим. Вообще переход от одного режима движения к другому происходит довольно плавно и охватывает большие диапазоны изменения числа Ra.

Для вычисления чисел подобия, входящих в уравнение (1) в качестве определяющей температуры (чтобы по справочникам найти λ;β;ρ;Pr;a) применяется средняя температура жидкости вдали от стенки. Исключение составляет число Pr_c, определяемое по температуре стенки.

Комплекс (Pr_ж/Pr_с)^0,25=ε_tтак же как и для вынужденного движения учитывает влияние направления и величины теплового потока на теплоотдачу.

Величины постоянных “C” и “n” зависят от режима свободного движения и расположения поверхности. Они определяются по опытным данным (аналогично как Nu=CRe^mPrⁿ в логарифмических координатах)

Так по опытным данным были получены следующие уравнения подобия вынужденного движения.

а ) Для горизонтальных труб при 10³<(Gr_ж;Pr_ж)<10⁹

(2)

Определяющий линейный размер , здесь d – диаметр трубы.

Для воздуха и 2 – х атомных газов ε_t≈1 и уравнение (2) существенно упрощается.

(3)

Уравнение (2) и (3) можно использовать и для горизонтальных плит. При этом в качестве определяющего линейного размера берут ширину плиты.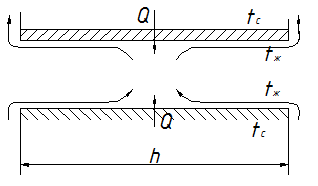


Опытно установлено, что определенный по уравнениям (2) и (3) коэффициент теплоотдачи α необходимо уменьшить на 30%, если теплоотдающая поверхность обращена вниз и увеличить на 30%, если вверх. Это объясняется тем, что первое положение плиты тормозит входящее движение потока, а второе ему способствует.

б) для вертикальных поверхностей

при 10³<(Gr_ж;Pr_ж)<10⁹- соответствует ламинарному режиму движения.

(3)

при (Gr_ж;Pr_ж)>6∙10⁶ - соответствует турбулентному режиму движения.


Определяющий линейный размер, в этих формулах, размер по вертикали (длина трубы или высота стенки).

в) при 10⁹<(Gr_ж;Pr_ж)<6∙10¹⁰- наблюдается переходный режим, в котором оценивается только приблизительно.

Примерные значения коэффициента теплоотдачи α при свободном движении в неограниченном объёме составляют:

- для воздуха и газов α=5 – 15 Вт/м²К

- для воды α=200 – 1000 Вт/м²К
2 .8.2 Свободная конвекция в ограниченном пространстве
При свободном движении в неограниченном объеме жидкости мы можем рассматривать всегда одно явление: например нагрев жидкости от стенки. Охлаждение при этом происходило где – то вдали и никак не влияло на рассматриваемое нами явление.



В малом ограниченном пространстве (прослойки, щели, кольцевые каналы)(полости для охлаждающей жидкости) явление нагревания и охлаждения жидкости протекают вблизи друг друга и разделить их невозможно (они влияют друг на друга) и поэтому весь процесс необходимо рассматривать в целом.

Вследствие ограниченности пространства и наличия восходящих и нисходящих потоков условия движения сильно усложняются. Они зависят как от формы и геометрических размеров канала, так от рода жидкости и интенсивности процесса теплообмена.

Около нагретой поверхности создается восходящее свободное движение, а около холодной нисходящее, которые зависят от ∆t,Pr,формы, размера, объема и толщины слоя жидкости δ.



В вертикальных каналах и щелях в зависимости от δ свободное движение жидкости может протекать по двум способам. Если “ δ ” достаточно велика, то входящий и нисходящий потоки движутся без взаимных помех. Их характер такой же, как и вдоль вертикальных поверхностей.

Если же “ δ ” мала, то вследствие взаимных помех восходящий и нисходящий потоки сливаются и образуют контуры циркуляции высотой h. Высота их определяется шириной щели δ: чем больше δ, тем меньшеh.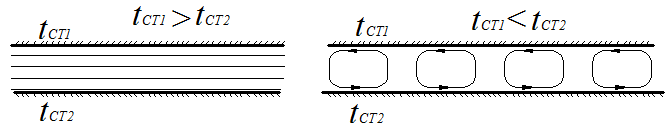


В горизонтальных щелях процесс помимо распространения между поверхностями зависит от взаимного расположения нагретых и холодных поверхностей. Если нагретая поверхность расположена сверху. То циркуляция совсем отсутствует.

Если нагретая поверхность расположена снизу, то процесс протекает аналогично процессу в вертикальной щели, но контуры циркуляции в них чередуются по направлению.


В шаровых и горизонтальных цилиндрических прослойках циркуляция жидкости, если нагрета внутренняя поверхность t₂>t₁ , развивается лишь в зоне лежащей выше нижней кромки нагретой поверхности. Ниже её жидкость остается в покое.

Если же нагрета внешняя цилиндрическая поверхность t₂<t₁, то циркуляция жидкости протекает в пространстве расположенной ниже верхней кромки холодной поверхности (вверху как для горизонтального канала).

Т.к. процессы нагревание и охлаждения в малых объемах протекают вблизи и разделить их невозможно, то применение обычных методов расчета теплоотдачи является затруднительным. (т.е. мы не можем пользоваться формулой Ньютона – Рихмана Q=α∆tF). Мы не можем в этих условиях установить правильную закономерность изменения α отдельно для нагревания и охлаждения.

Как быть? А для этого применяют специальные методики.

Для упрощения исследования конвективного теплообмена через прослойки, этот сложный процесс, рассматривают как явление передачи теплоты путем теплопроводности, вводя при этом понятие эквивалентного коэффициента теплопроводности:

- плоская прослойка.
- цилиндрическая прослойка.

где F – поверхность теплообмена (F=F₁=F₂)

l– длина прослойки

λ_экв– эквивалентный коэффициент теплопроводности.

Q_к – тепловой поток передаваемый конвекцией через прослойку.

λ_экв=λε_к

где λ– действительный коэффициент теплопроводности жидкости или газа в прослойке.

- коэффициент конвекции, учитывающий влияние конвекции на перенос теплоты через прослойку.

Т.к. циркуляция жидкости обуславливает разность плотностей нагретых и холодных частиц и определяется критерием (Gr_ж;Pr_ж), то ε_к должно являться функцией этого же аргумента ε_к =f(Gr_ж;Pr_ж).

Коэффициент конвекции ε_к определяется по опытным данным и представляется в виде обобщенного уравнения подобия. В приближенных расчетах для ((Gr_ж;Pr_ж)>10³) для любой жидкости или газа можно воспользоваться уравнением:

ε_к=0,18(Gr_ж;Pr_ж)^0,25

В этом уравнении при определении числа Грасгофа в качестве определяющего линейного размера выступает ширина канала δ, а определяющее температурное поле t_ж=t_cт1+t_ст2.

В тех случаях, когда прослойка заполнена газом, теплота наряду с конвекцией передается через нее и радиацией (лучистым теплообменом). В этом случае полный тепловой поток определиться как Q=Q_к+Q_л



где С_п – приведенная излучательная способность системы тел.

T_ст1 и T_cт2– абсолютные температуры стенок (не в коем случае не в ⁰С)