Лекции по теплопередачи (Конвективный теплообмен, Word). 2. конвективный теплообмен основные понятия и определения

• Название: 2. конвективный теплообмен основные понятия и определения
• Дата: 04.11.2022
• Размер: 1.22 Mb.
• Имя файла: Лекции по теплопередачи (Конвективный теплообмен, Word).doc
• Тип: Документы; #770565
• страница: 6 из 7

2.7.3 Теплоотдача при поперечном обтекании труб.


Итак рассмотрим 2 задачи поперечного набегания потока жидкости (газа) на одиночные трубы и пучки труб. Опыт показывает, что теплоотдача в этом случае существенно интенсивнее чем при продольном обтекании трубы или пучка труб. Почему? Ну во-первых более эффективно работает поверхность теплообмена (при продольном обтекании по мере движения вдоль трубы ∆t падает и интенсивность теплообмена тоже, при поперечном обтекании поверхность работает более равномерно) и во- вторых это связано со структурой потока при поперечном обтекании трубы, отличной от случая продольного обтекания. Её мы рассмотрим на примере одиночной трубы.

Вследствие большей интенсивности теплоотдачи поперечное обтекание труб нашло широкое применение в практике конструировании теплообменных аппаратов (радиатор автомобиля, котел и т. д.) .

Для расчетов коэффициентов теплоотдачи “α” при поперечном обтекании труб получены достаточно надежные уравнения подобия. При их использовании надо рассчитать два основных случая: обтекание одиночной трубы и обтекание пучка труб.
2.7.3.1 Теплоотдача при обтекании одиночной трубы.

Пусть одиночная труба находиться в поперечном потоке набегающей жидкости со скоростью ω. Средняя температура набегающего потока жидкости равна t_ж.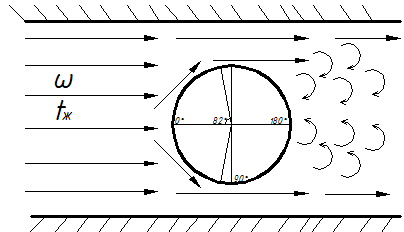



Движение жидкости у поверхности трубы является сложным. Его характер не одинаков на передней боковой (90⁰) и задней (180⁰) половинках цилиндра трубы.

Поток жидкости набегает на цилиндр в лобовой части и начинает его обтекать. Вдоль поверхности трубы образуется ламинарный пограничный слой. В районе экватора боковой поверхности (точнее при угле 82⁰) происходит отрыв струи от поверхности трубы и возникают вихревые турбулентные структуры. Следовательно только 45% поверхности трубы омывается потоком жидкости безотрывно, остальная часть её находится в вихревой зоне со сложным циркуляционным течение.

Такая своеобразная картина обтекания одиночной трубы в сильной мере отображается и на теплоотдаче.

На лобовой части трубы (0⁰) (где поток жидкости набегает на неё), коэффициент теплоотдачи α имеет максимальное значение (от удара разрушается ламинарный пограничный слой).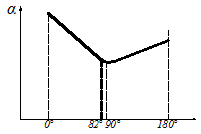



Далее по мере обтекания боковой поверхности до угла в 82⁰ коэффициент теплоотдачи уменьшается вследствие роста ламинарного пограничного слоя. В кормовой части трубы он вновь несколько возрастает, так как здесь наблюдается отрыв потока и образование вихревых структур.

В литературе вы можете найти обширные опытные данные как по значениям местных коэффициентов теплоотдачи при поперечном обтекании труб, так и по их средним значениям по всей поверхности трубы. Последние представляют наибольший интерес в технических расчетов.

Вообще, при поперечном обтекании труб в теплообмене учувствует лишь тонкий, прилегающий к поверхности слой жидкости. Но так как этот слой от остальной жидкости не отделен, то процесс теплоотдачи сильно зависит от характера движения всей массы жидкости, угла атаки, диаметра трубы и ряда других факторов.

Для определения средних значений α по периметру одиночной трубы можно рекомендовать следующие критериальное уравнение подобия: 10³<Re<2∙10⁵.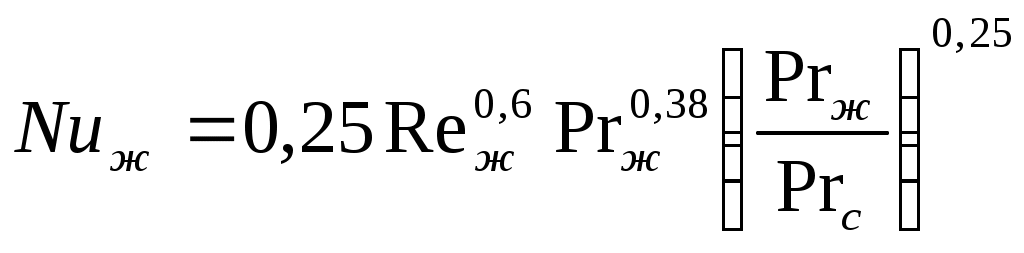

(7)

Это уравнение справедливо для жидкостей и газов. Учитывая, что для газов Pr_ж=const уравнение (7) можно упростить, так для воздуха и 2 – х атомных газов.

(7а)

В этих уравнениях в качестве определяющей температуры принята температура набегающего потока 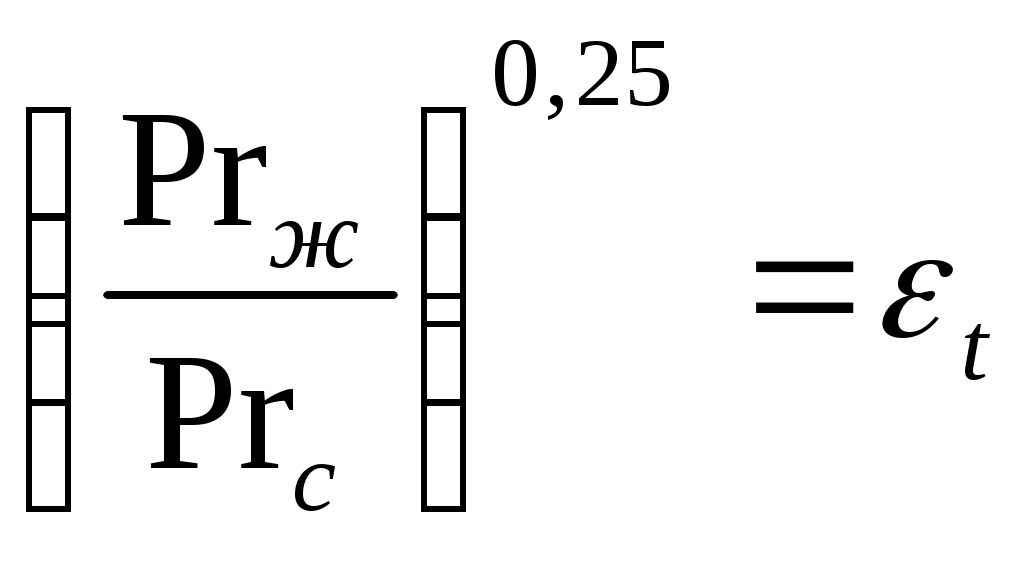, определяющий линейный размер – наружный диаметр трубы d_н

- учитывает влияние на уравнение теплообмена, при направлении выше чем при охлаждении жидкости.

Из уравнения (7) мы видим, что при поперечном обтекании одиночной трубы коэффициент теплоотдачи потока зависит от скорости ω, физических свойств Pr_ж, диаметра трубы (с уменьшением диаметра трубы интенсивность теплоотдачи растет). Кроме того при поперечном обтекании коэффициент теплоотдачи α существенно зависит от угла атака φ (т.е. от направления потока жидкости по отношению к оси трубы ).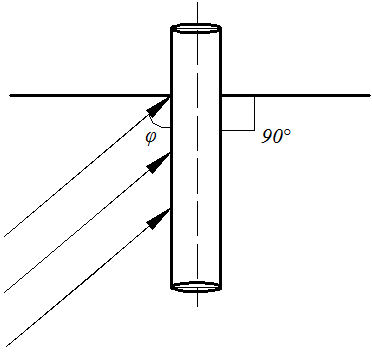



Приведенные уравнения (7) и (7а) справедливы для угла атаки φ=90⁰. Если φ<90⁰ то αуменьшается. Поэтому полученный из уравнения (7) коэффициент теплоотдачи необходимо домножать на поправочный коэффициент ε_φ<1. (Например для φ=45⁰, ε_φ =0,8). Значение его берется из специальных графиков.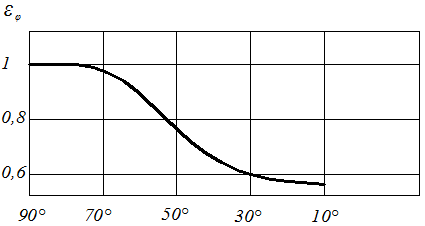


Из графика видно, что худшим случаем теплоотдачи будет продольное обтекание трубы (φ=0⁰).

Теперь рассмотрим поперечное обтекание пучка труб.
2.7.3.2 Поперечное обтекание пучка труб.
Процесс теплоотдачи еще более усложняется, если в поперечном потоке жидкости имеется не одна, а целый пучок (пакет) труб. По такому принципу построены большинство теплообменных аппаратов (радиаторы автомобиля). Применение пакетов труб позволяет создавать больше поверхности теплообмена при малых габаритах аппарата.

Характер движения жидкости, а следовательно и теплоотдача пакетов тру во многом зависит от их компоновки. По расположению труб пучки разделяются на коридорные и шахматные.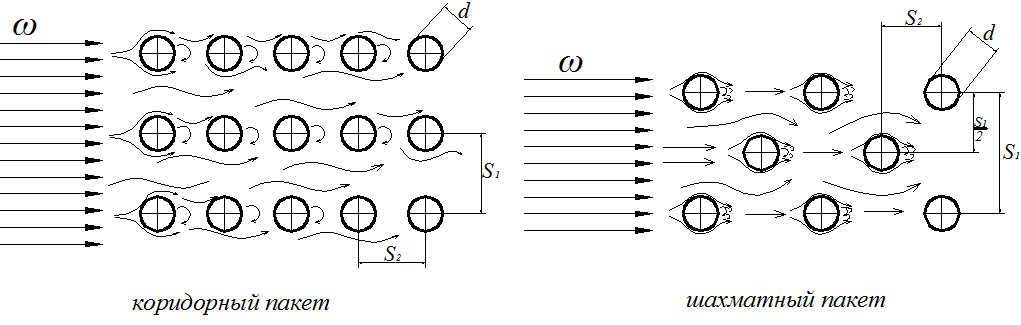



Геометрическими характеристиками пучка является наружный диаметр трубок d и относительный шаг , где S₁- поперечный шаг, S₂- продольный шаг.

Условия омывания первого ряда трубок в обоих случаях близки к омыванию одиночной трубки. Для последующих же рядов характер омывания существенно омывается.

В коридорном пучке все трубки второго и последующих рядов находятся в вихревой зоне впереди стоящих, между трубками по глубине пука получается застойная зона с относительно слабой циркуляцией жидкости. Поэтому здесь как лобовая, так и кормовая части трубок омываются менее интенсивнее, чем у одиночных трубок или трубок первого ряда.

В шахматном пучке омывание глубоко расположенных трубок мало чем отличается от омывания первого ряда.

Такие режимы обтекания пучков труб накладывают своё влияние на изменение местного коэффициента теплоотдачи по поверхности трубок различных рядов.

Для первого ряда коридорных и шахматных пучков изменение α по окружности трубы носит такой же характер, как и для одиночной трубы.

Для второго и последующих рядов коридорного пучка max α находится не в лобовой точке, а под углом 50⁰ от нее (т.е. в той точке, где происходит удар набегающих струй). Лобовая часть непосредственному омыванию потоком не подвержена. В шахматных пучках maxтеплоотдачи для всех рядов труб приходиться на лобовую точку.

Вообще в пучках труб α зависит от скорости потока, физических свойств жидкости, расположения трубок и числа рядов.

На основе обобщения опытных данных было установлено, что теплоотдача первого ряда в пучке труб определяется начальной турбулентностью потока. Теплоотдача второго и третьего рядов по сравнению с первым возрастает. Если теплоотдачу третьего ряда принять за 100%, то в шахматном и коридорном пучках теплоотдача первого ряда составит 60%, а второго в коридорном – 90%, в шахматном – 70%.

Причиной возрастания теплоотдачи является увеличение турбулентности потока при прохождении его через пучок. Начиная с третьего ряда турбулентность потока принимает стабильный характер, присущий данной компоновке пучка.

Установлено, что по абсолютному значению теплоотдача в шахматных пучках выше, чем в коридорных, что обусловлено лучшим перемешиванием жидкости в них α_ш> α_к.

Для расчетов коэффициентов теплоотдачи в пучках труб рекомендовано следующее уравнение подобия: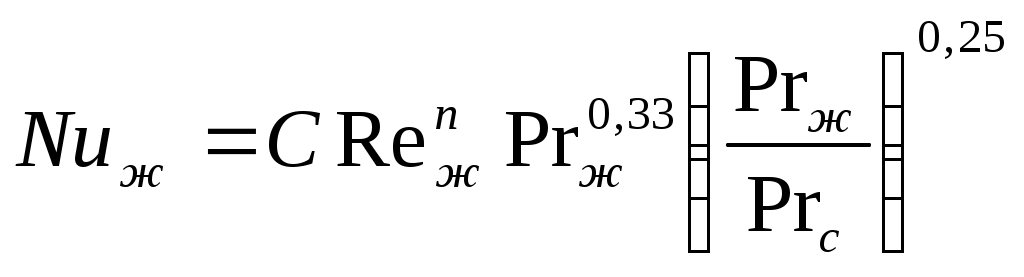
(8)

С=0,23; n=0,65 – для коридорного пучка

С=0,41; n=0,6 – для шахматного пучка

Это уравнение применимо для расчета всех жидкостей и газов при значениях от 10³<Re<2*10⁵. Для воздуха и 2-х атомных газов оно примет вид:

- коридорные пучки

- шахматные пучки (8а)

В качестве определяющей температуры в них принята средняя температура жидкости в пучке t_ж :

t_ж=0,5(t’+t”),

где t’ - температура жидкости на входе в пучок

t”- температура жидкости на выходе из пучка.

В качестве определяющего линейного размера используется внешний диаметр труб. Скорость потока определяется в самом узком сечении пучка .

Уравнения (8) и (8а) позволяют определить коэффициент теплоотдачи α для третьего и последующего рядов труб. Для труб первого ряда полученная величина умножается но коэффициент 0,6 (60%), а для тркб второго ряда на 09 (90%) для коридорного пучка и 0,7(70%) для шахматного.

Средняя величина для пучка в целом определяется по формуле:

(9)

где α₁; α₂… α_n- коэффициенты теплоотдачи по рядам

F₁; F₂… F_n - площади поверхностей труб в рядах

n - число рядов

если F₁=F=₂…=F_n,

(9а)

Полученная величина α_пуч относится к случаю набегания потока на пучок при угле атаке φ=90⁰. Если φ<90⁰, то полученную величину α_пуч умножают на множитель ε’_φ<1 для пучка, отличную от ε_φ для одиночной трубы. Учитывая особую важность поперечного обтекания пучков, для тепловых машин и аппаратов рассмотрим небольшой числовой пример:

Воздухонагреватель предполагается выполнить из труб диаметром 38 мм, распложенных в коридорном порядке число труб в одном ряду 8, число рядов 5. Температура воздуха поступающего в подогреватель 20⁰С, на выходе 80⁰С. Температура стенок труб 150⁰С. Какой длины должны быть трубы, чтобы при скорости воздуха в узком сечение пучка ω=10 м/c тепловой поток составил бы Q=112 КВт

d = 38 t’=200C t”=800C tcт=1500C ω=10 м/c Q=112КВт

l-?

1) Найдем определяющую температуру t_ж=0,5(20+80)=50⁰C средняя температура воздуха в пучке.

2)По определяющей температуре воздуха найдем его физические параметры (по таблицам)

λ_ж=2,43∙10^-2 Вт/мК

υ_ж=17,95∙10^-6 м²/с

3)Определяем число Рейнольдса

Re=(ωd)/υ=(10∙0,038)/17,95∙10^-6=21200

4)По формуле для коридорного пучка (8а) находим число Нуссельта (т.к. 10³5)

Nu_ж=0,216Re^0,65=0,216∙21200^0,65=136

5)Определим коэффициент теплоотдачи для 3,4,5 рядов

α_3,4,5=Nu_ж(λ/d)=136(2,43∙10^-2/0,038)=87 Вт/м²К

6)Определим α для 1 – ого и 2 – ого рядов

α₁= α_3,4,5∙0,6=87∙0,6=52,2 Вт/м²К
α₂= α_3,4,5∙0,9=87∙0,9=78,3 Вт/м²К
7)Определим средний коэффициент теплоотдачи для пучка, т .к. F₁=F₂=…=F₅ формула (9) упрощается


8)Определим плотность теплового потока в пучке

q=α(t_c-t_ж)=78,5(150-50)=7850 Вт/м²

9)Определим потребную поверхность трубок



10)Определим длину трубок у воздухонагревателя



z=8∙5=40- число трубок.
2.7.3.3 Особенности расчета коэффициента теплоотдачи при поперечном обтекании пучка оребрённых труб.



Одним из недостатков гладкотрубных теплообменных аппаратов с поперечным омыванием пакета труб являются не высокие коэффициенты теплоотдачи при течении там газов и вязких жидкостей. Этот недостаток влечет за собой существенные увеличения габаритов и массы аппарата.

Компактные теплообменники в этом случае получаются при применении пучков оребренных труб (ленты, пластины, проволочные наклейки, батареи в новых домах).

Наличие оребренных труб в потоке жидкости или газа во – первых, увеличивает поверхность теплообмена, а во – вторых, интенсифицирует теплоотдачу благодаря дополнительной турбулизации потока. Q=α∆tF



Поэтому при поперечном омывании пучка оребренных труб теплоотдача в них зависит не только от компоновки (шахматная или коридорная). Но и от формы, высоты ребер и шага между ними.

Опытом установлено, что с ростом высоты ребер вследствие снижения их тепловой эффективности α понижается. Поэтому в потоках вязкой жидкости наиболее эффективна малая высота ребер. Однако, для газов повышение при уменьшении h_p не компенсирует уменьшение теплоотдачи от удлинения поверхности теплообмена.

Оптимальный размер шага между ребрами колеблется в пределах

t_p=(0,2-0,4)d_тр Уменьшение t_p приводит к уменьшению α, т.к. между ребрами появляются зоны со слабой циркуляцией.

На интенсивность теплоотдачи в пучках оребренных труб значительное влияние оказывает и толщина ребер δ_р. Оптимальнее δ_р по опытным данным составляет 0,5 мм. Увеличение её приводит к ухудшению массовых показателей.

Экспериментальное исследование теплоотдачи в пучках оребренных труб связано с большими трудностями при определении температурных полей в ребрах. Поэтому для упрощения исследований вводится понятие приведенного коэффициента теплоотдачи . Суть его заключается в том, что оребренную поверхность сводят к равновеликой гладкой, а действительные условия эксперимента заменят фиктивными, хотя и эквивалентными по суммарным результатам.

Однако, уравнения подобия выведенные для определения 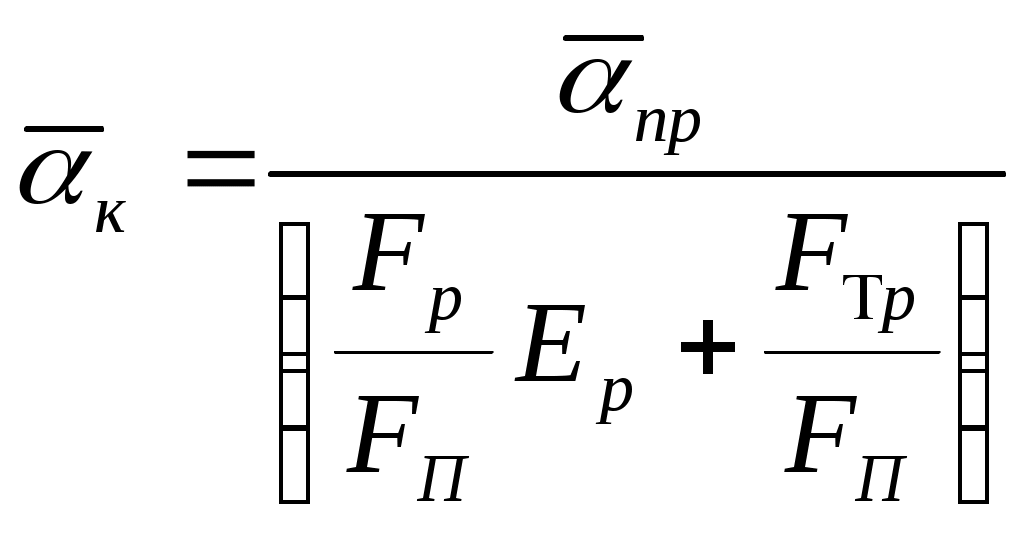имеют ограниченное применение, т.к. справедливы только для тех условий, в которых проводиться эксперимент. Для того, чтобы результаты единичного эксперимента можно было распространять на целый класс явлений используют конвективный коэффициент теплоотдачи , который учитывает термическое сопротивление собственно ребер. Тепловой поток, при определении относится к разности температур между теплоносителем (t_ж) и определенной температурой оребреннных и неоребренных поверхностей трубы

,

где F_p- площадь поверхности ребер на единице длины трубы

F_П - полная площадь поверхности оребренной трубы F_П=F_р+F_тр

F_тр- площадь поверхности трубы.

E_p - коэффициент эффективности ребер, характеризующий их термическое сопротивление E_p=f(t_p;h_p;Ф). Он определяется как отношение теплового потока, проходящего через оребренную поверхность, к тому Q, который мог бы через нее проходить при .

Различные выражения определения E_p и уравнения подобия для расчета поперечного обтекания пучков оребренных труб вы можете, при необходимости, найти в литературе (Селиверстов стр.200)