Лекции по теплопередачи (Конвективный теплообмен, Word). 2. конвективный теплообмен основные понятия и определения

• Название: 2. конвективный теплообмен основные понятия и определения
• Дата: 04.11.2022
• Размер: 1.22 Mb.
• Имя файла: Лекции по теплопередачи (Конвективный теплообмен, Word).doc
• Тип: Документы; #770565
• страница: 1 из 7

2. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

2.1. Основные понятия и определения

Под конвекцией понимают распространение теплоты в среде с неоднородным распределением температуры, осуществляемое макроскопическими частицами жидкости при ее перемещении.

Как мы уже с вами отмечаем, в чистом виде конвекция в природе не встречается, а всегда сопровождается теплопроводностью. Поэтому можно дать следующее определение конвективному теплообмену.

Конвективный теплообмен это совместный процесс переноса теплоты теплопроводностью и конвекцией в движущейся жидкости или газе.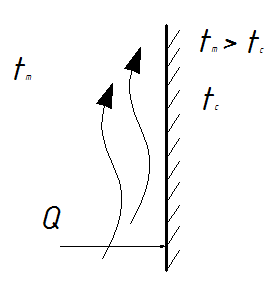



Для практики наибольший интерес представляет случай конветивного теплообмена между твердым телом и соприкасающейся с ним жидкостью или газом. (Например радиатор автомобиля, батарея отопления дома, холодильник, отопление кабины и т. д.) Этот процесс называется конвективной теплоотдачей или просто теплоотдачей.

Процесс конвективной теплоотдачи имеет наиболее широкое в тепловых машинах и аппаратах и является весьма сложным. Он зависит от многих факторов, основными из которых являются

1.Теплоотдача зависит от физических свойств температуры теплоносителя (жидкости) “t_ж” и стенки “t_ст ”

Непосредственно на теплоотдачу имеют влияние следующие физические свойства жидкости (теплоносителя):

– λ, - коэффициент теплопроводности;

– C_p, - теплоемкость;

– ρ, - плотность жидкости;

– , - коэффициент температуропроводности, он характеризует темп изменения в различных точках жидкости по времени при нестационарных процессах;

– вязкость жидкости – которая характеризует силы внутреннего трения между слоями жидкости. Различают динамический и кинематический коэффициенты вязкости.

µ, - динамический коэффициент вязкости;

ν=µ/ρ, - кинематический коэффициент вязкости;

– коэффициент объемного расширения – он характеризует относительное изменение объема при нагревании жидкости на 1 К при p=const Для идеальных газов , .

Перечисленные физические свойства для различных теплоносителей различны. Их значение приводятся в справочниках. При выборе их необходимо учитывать, что все они зависят от Т, а некоторые от давления p. Так например µ для капельных жидкостей с повышением температуры уменьшается, а для газов увеличивается.

2. Теплоотдача зависит от природы возникновения и режима движения жидкости. Это связано с тем, что конвективный теплообмен зависит от распределения температур в потоке. В свою очередь характер температурного поля определяется распределением скоростей в потоке, т.е. скоростным полем, зависящем от режима течения.

По природе возникновения различают вынужденное и свободное движение жидкости.

Свободное движение возникает за счет разности плотностей холодных и нагретых частей жидкости под действием гравитационных сил. (например вокруг нагретой трубы или над плитой наблюдается свободное движение воздуха вверх)

Вынужденное движение вызывается вентиляторами, насосами и другими возбудителями движения. Вынужденное движение всегда сопровождается свободным, однако при больших скоростях последним можно пренебречь.

При перемещении жидкости возможны 2 основных режима течения: ламинарный и турбулентный.

При ламинарном движении отдельные струйки жидкости, перемещаясь в одном и том же направлении не перемешиваются (все частицы движутся параллельно стенкам канала в одном направлении).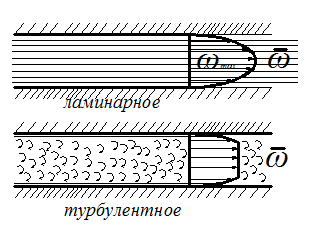



При турбулентном режиме течения каждая частица потока, участвующая в общем поступательном движении, кроме того совершает и различные поперечные движения (происходит постоянные пульсации значения 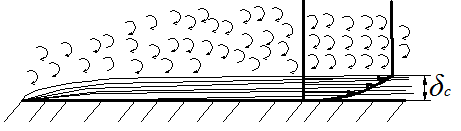и изменения их мгновенных направлений). При пульсации скорости и перемещения вихрей из одной области течения в другую происходит перенос механической энергии. Если в движущемся потоке наблюдается неоднородность t поля, то упомянутые явления приводят к переносу теплоты в следствии чего наблюдаются и температурные пульсации.



Однако при турбулентном режиме не вся масса жидкости движется завихренно. Около стенки из – за вязкого трения жидкости возникает ламинарный пограничный слой.

Этот пограничный слой, в котором скорость потока меняется от “0” на стенке до скорости основного потока называется гидродинамическим пограничным слоем.

Для него характерны малая толщина и большие поперечные градиенты скорости.

Режим движения жидкости и толщина пограничного слоя зависят от скорости потока (Re<2000- ламинарный; Re>10⁴ - турбулентный); диаметра (размеров) канала, плотности ρ и вязкости µ жидкости.

Режим движения жидкости определяет механизм переноса теплоты. При ламинарном движении теплота от потока жидкости к стенке переносится только теплопроводностью, т.к. частицы жидкости движутся параллельно стенкам. Учитывая малые значения коэффициента теплопроводности λ для жидкостей и газов можно сделать вывод, что при ламинарном режиме теплоотдача будет слабой.

При турбулентном режиме течения, благодаря перемешиванию жидкости теплота переносится конвекцией и теплопроводностью. Теплоотдача в этом случае будет более интенсивной. Однако огромное влияние на нее будет оказывать ламинарный пограничный подслой. Он будет составлять основное термическое сопротивление и задерживать теплоотдачу. Чем меньше δ_r - тем интенсивнее теплоотдача.

Наряду с гидродинамическим пограничным слоем в потоке может образовываться и тепловой пограничный слой. Это слой жидкости или газа непосредственно участвующий в теплоотдаче, благодаря чему температура в этом слое меняется от t_cт до t_ж. Тепловой пограничный слой характеризуется большим поперечным градиентом температуры, под действием которого и осуществляется перенос теплоты.

Тепловой пограничный слой может не совпадать по толщине с гидродинамическим. Например у вязких жидкостей толщина теплового пограничного слоя значительно меньше чем гидродинамического. У газов они практически совпадают.

3. Теплоотдача зависит от t_cт - температуры твердой стенки, её размеров (площади поверхностей) и расположения её по отношению к потоку жидкости.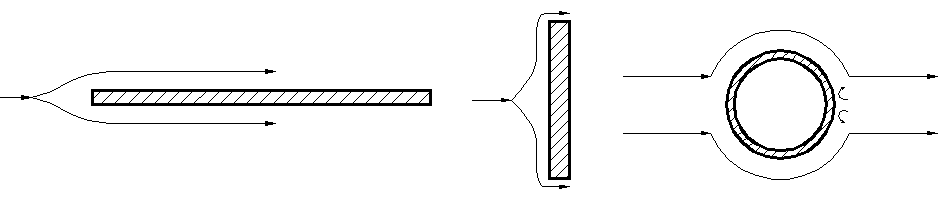



т.е. форма и расположение поверхности по отношению к потоку жидкости могут быть разными. В каждом конкретном случае возникают разные режимы течения и режимы теплоотдачи будут разными.

Таким образом мы можем сделать вывод, что тепловой поток при конвективной теплоотдаче является сложной функцией многих переменных.

Q=f(ω;t_c;t_ж;λ;ρ;C_p;α;β;µ;l­₁;l₂;…;F­)


2.1. Уравнение Ньютона – Рихмана
При проектировании каналов и устройств важно правильно оценивать гидродинамическую обстановку (ламинарное или турбулентное течение), потому, что интенсивность теплоотдачи во многом зависит от структуры и толщины пограничного слоя.

Поверхностная плотность теплового потока для случая ламинарного пограничного слоя может быть определена по закону Фурье
(74)

Однако в большинстве случаев не представляется возможным определить градиент температуры в пограничном слое, а следовательно и определить по формуле (74). Для турбулентного пограничного слоя эта формула вообще не приемлема.

Поэтому в основу расчета конвективного теплообмена принят закон Ньютона Рихмана: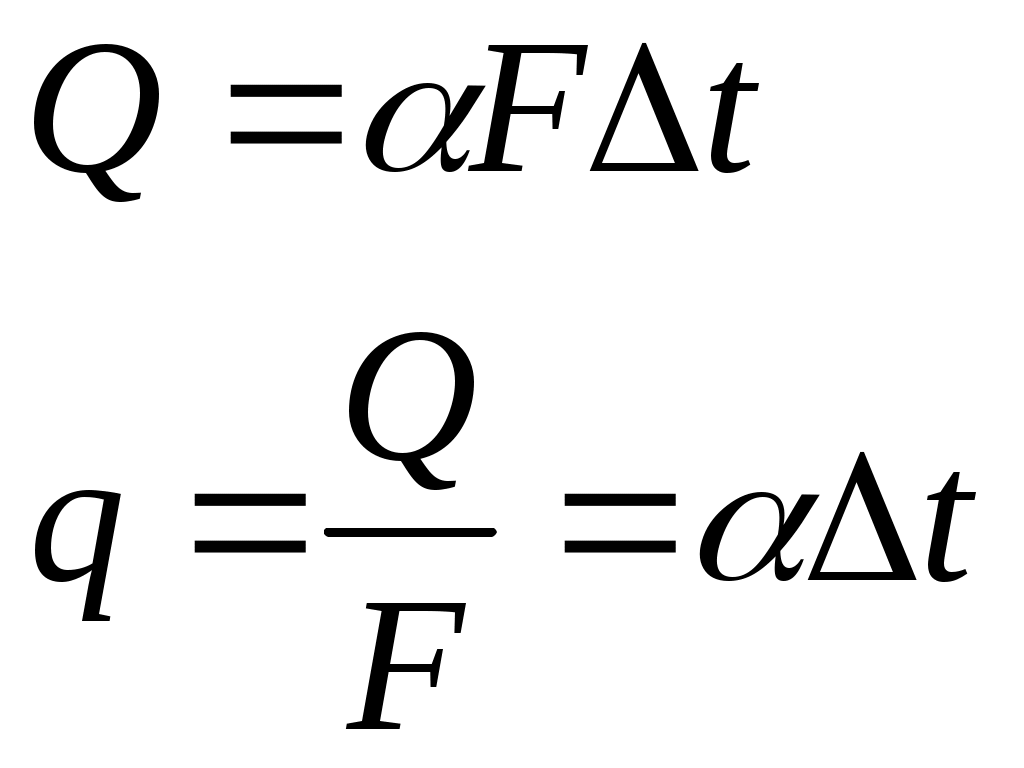
(75)

где, ∆t=t_ж-t_c- средняя разность температур между жидкой и твердой стенкой на всей площади поверхности.

F- поверхность теплообмена

- коэффициент теплоотдачи, характеризующий её интенсивность.

Численно коэффициент теплоотдачи равен тепловому потоку, передаваемому в единицу времени через единицу поверхности при разности температур стенки и жидкости в 1 К.


(76)

Эта количественная характеристика процесса теплоотдачи учитывает его конкретные условия.

Опыт показывает, что α меняется от 0 до 200000

Приведенное нами уравнение (75) было предложено Ньютоном для случая теплообмена в свободном потоке при условии, что зависит только от физических свойств тела и среды. В действительности же коэффициент теплоотдачи , в отличие от коэффициента теплопроводности не является величиной постоянной, а зависит от множества факторов, тех же от которых зависит и тепловой поток Q

α=f(ω;t_c;t_ж;λ;ρ;C_p;α;β;µ;l­₁;l₂;…;F­)
Производить расчеты по формуле Ньютона – Рихмана можно только после того, как определен . А в этом заключается основная сложность расчета коэффициента теплоотдачи.

Изучение теплоотдачи ведется двумя взаимосвязанными методами: аналитическим и экспериментальным (опытным)

При аналитическом методе изучения ведется на основе дифференциальных уравнений конвективного теплообмена.

1. 
   
   
2. 
   
   
3. 
   
   

4. 
   
   

2.2. Дифференциальные уравнения конвективного теплообмена
Любой физический процесс можно описать дифференциальным уравнением (или интегральным). Учитывая, что теплоотдача осуществляется и теплопроводностью, и конвекцией, зависит не только от температурных условий, но и от характера движения жидкости, поэтому она описывается не одним дифференциальным уравнением, а системой дифференциальных уравнений в которую входят:

- уравнение теплообмена на границе раздела сред;

- дифференциальное уравнение энергии;

- дифференциальное уравнение движения жидкости;

- дифференциальное уравнение неразрывности.


2.2.1. Уравнение теплообмена на границе раздела сред.
Уравнение теплообмена должно характеризовать теплообмен на границе соприкосновения твердого тела и жидкости.


Его можно составить исходя из свойств пограничного ламинарного слоя жидкости, который имеется как при ламинарном и при турбулентном режиме течения.

Учитывая, что в нём нет перемешивания жидкости и теплота передается через него только теплопроводностью по нормали к поверхности к твердому телу плотность теплового потока можно определить по закону Фурье

(77)

λ_ж - коэффициент теплопроводности жидкости

- градиент температуры в пограничном слое

Кроме того плотность теплового потока, передаваемую через пограничный слой можно выразить и через закон Ньютона – Рихмана

q=α∆t (78)

где ∆t=t_с-t_ж

Приравнивая правые части уравнений (77) и (78) мы получим уравнение теплообмена.
(79)

Уравнение (79) связывает коэффициент теплоотдачи α с условиями теплообмена в пограничном слое, т. е. с градиентом температуры.



Для того, чтобы по уравнению (79) определить необходимо знать gradt, для определения которого нужно знать температурное поле в жидкости. Его нам поможет определить дифференциальное уравнение энергии (или уравнение Фурье – Каргофа – теплопроводность в движущейся жидкости )
2.2.2. Дифференциальное уравнение энергии.
Это уравнение является математическим выражением закона сохранения энергии в процессе теплоотдачи и устанавливает зависимость

t=f(x,y,z,τ)

т. е. позволяет определить температурное поле в движущейся жидкости.

Для вывода уравнения энергии выделим из движущегося объема жидкости элементарный объем

dV=dxdydz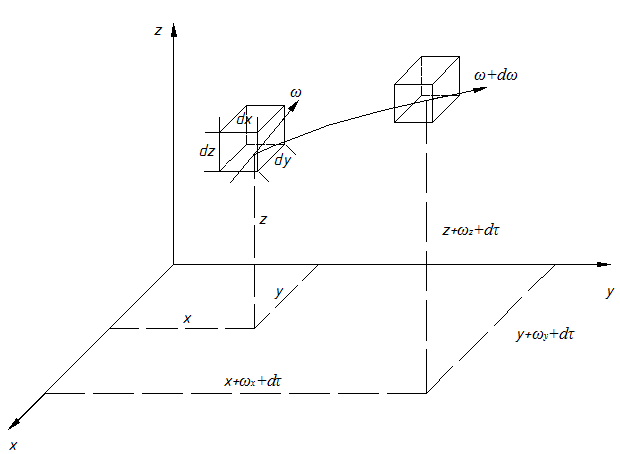



Из окружающей среды путем теплопроводности в элементарный объем в dVза время dτ согласно дифференциального уравнения теплопроводности (19) поступит теплота

(80)

Аналогично тому как мы с вами выводили дифференциальное уравнение теплопроводности поступившая в элементарный параллепипед теплота пойдет на изменение его энтальпии dQ=dI(среда движется)

Изменение энтальпии, рассматриваемого параллепипеда за время dτ определиться как:

(81)

Однако в предыдущем случае мы имели дело с твердым телом. В жидкости, в отличие от твердого тела, объём за время переместиться в пространстве по некоторой траектории со скоростью . Поэтому координаты рассматриваемого объёма будут изменяться во времени:

x=f(τ); y=f(τ); z=f(τ) и следовательно изменение tэлемента dV за время dτ будет характеризоваться полной производной:

(82)

изменение координат по времени есть ничто иное как проекции скорости на оси координат



таким образом уравнение (82) примет вид:

(83)

Отметим, что полную производную субстанциональной (индивидуальной) производной. Частную производную называют местным или локальным изменением температуры, а - конвективным изменением температуры.

Приравнивая значения dQ=dI получим искомое дифференциальное уравнение энергии, описывающее температурное поле в движущейся жидкости.






(84)

Данное уравнение (84) называется законом энергии, т. к. оно выражает закон сохранения энергии.

В том случае, когда ω_x=0; ω_y=0; ω_z=0 то конвективная составляющая в уравнении (84) исчезает и уравнение принимает вид дифференциального уравнения теплопроводности для твердых тел.

Для одномерного случая уравнение принимает вид:

(85),

а для одномерного стационарного случая имеем

(86)

В уравнении (84) наряду с tвходят проекции переменной скорости ϖ. Это показывает, что температурное поле в потоке жидкости существенно зависит от поля скоростей. В связи с этим необходимо при изучении конвективного теплообмена включить в круг исследуемых вопросов и гидростатические условия протекания процесса.

Наличие температурного поля в свою очередь изменяет плотность среды в следствии чего жидкость приходит в движение. Видим, что помимо влияния поля скоростей на температурное поле наблюдается и обратное влияние.

Поэтому необходимо добавить к уже имеющимся дифференциальным уравнением теплообмена и энергии уравнение движения жидкости.