Лекции по теплопередачи (Конвективный теплообмен, Word). 2. конвективный теплообмен основные понятия и определения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
2.5 Условия подобия процессов конвективного теплообмена. Теперь подробнее рассмотрим применение теории подобия к анализу процессов конвективного теплообмена. Так как в систему уравнений описывающих данный процесс входит: данный процесс описывается системой гидромеханических и тепловых дифференциальных уравнений (первые - дифференциальные уравнения и уравнения сплошности, вторые – уравнения энергии и уравнения теплообмена), то условия гидромеханического и теплового подобия мы рассмотрим раздельно. 2.5.1 Условия гидромеханического подобия. Как мы уже отмечали на процессе теплоотдачи существенное влияние оказывает характер движения жидкости (газа). Поэтому, для достижения подобия в процессах теплоотдачи в первую очередь необходимо наличие подобия в процессах движения или иначе гидромеханического подобия. Гидромеханическое подобие определяет собой условия, при которых в геометрически подобных системах осуществляются подобные движения. Движение вязкой несжимаемой жидкости (как мы уже установили) описывается дифференциальным уравнением Навье – Стокса (дифференциальное уравнение). Воспользуемся этим уравнением для выяснения условий гидромеханического подобия и вывода основных критериальных чисел подобия. Запишем уравнение Навье – Стокса для двух подобных процессов. Перемещение первого обозначим «’», а второго «”». Для упрощения рассмотрим его проекцию на ось х (можно любую другую): 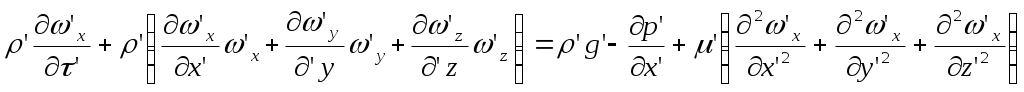 (1) (1)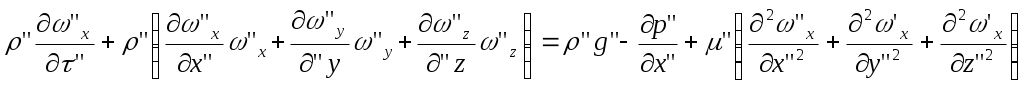 (2) (2)Мы уже знаем, что для подобных процессов отношение сходственных величин постоянны и равны соответствующим константам подобия 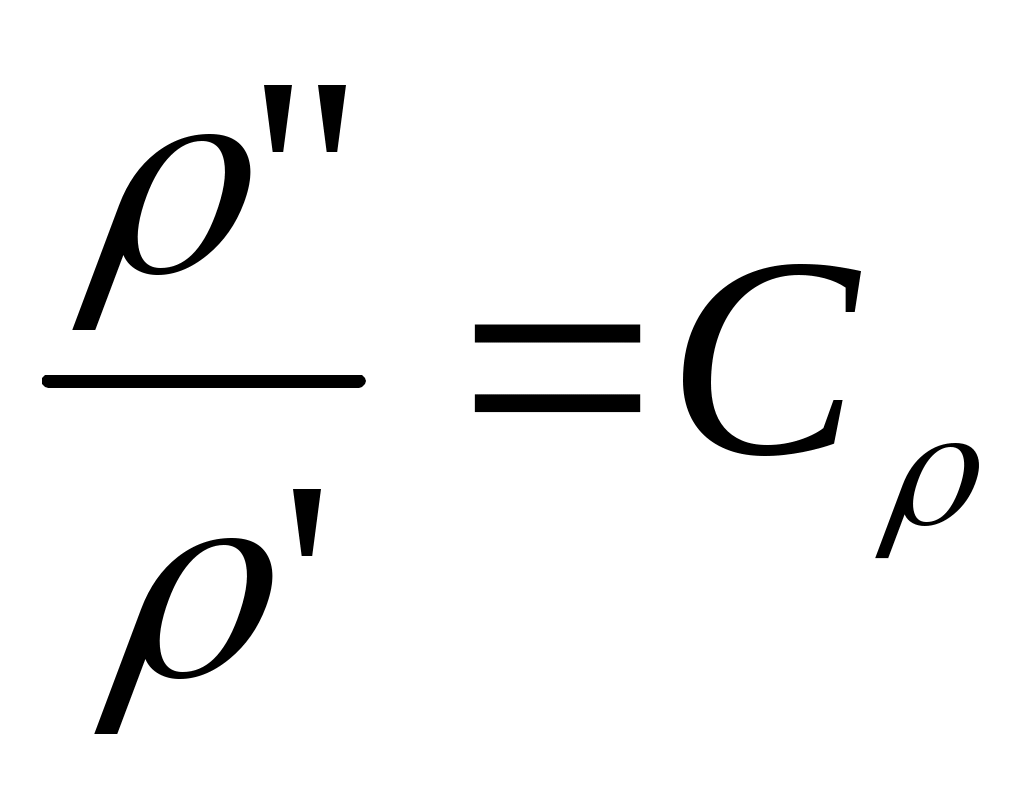 ; ;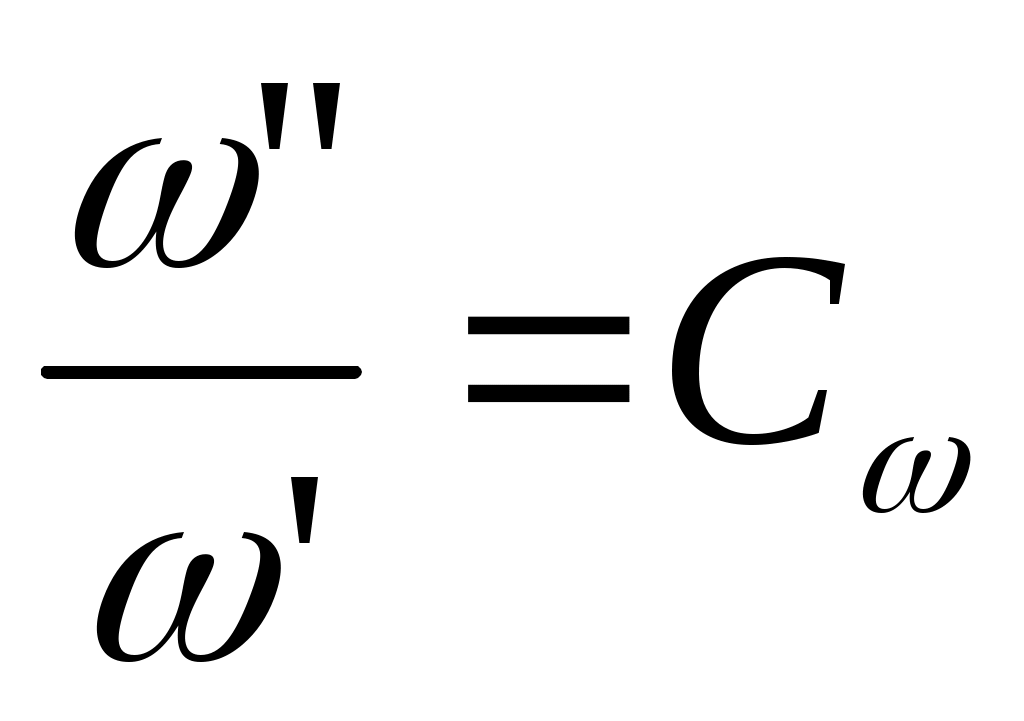 ; ;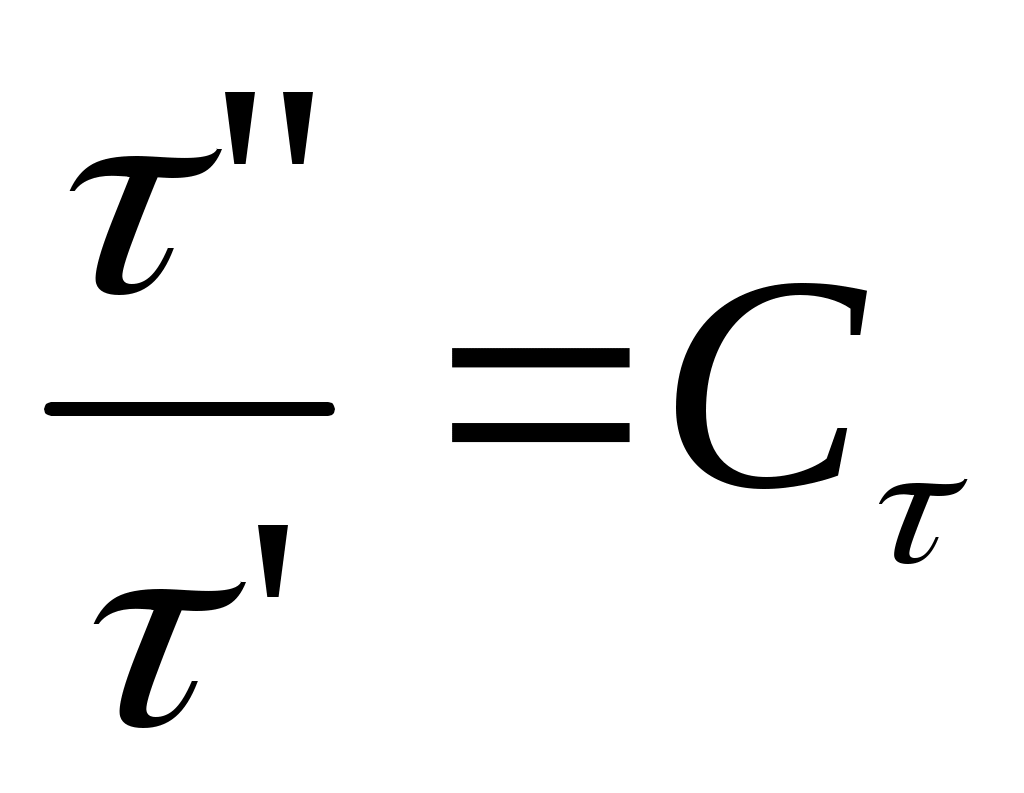 ; ;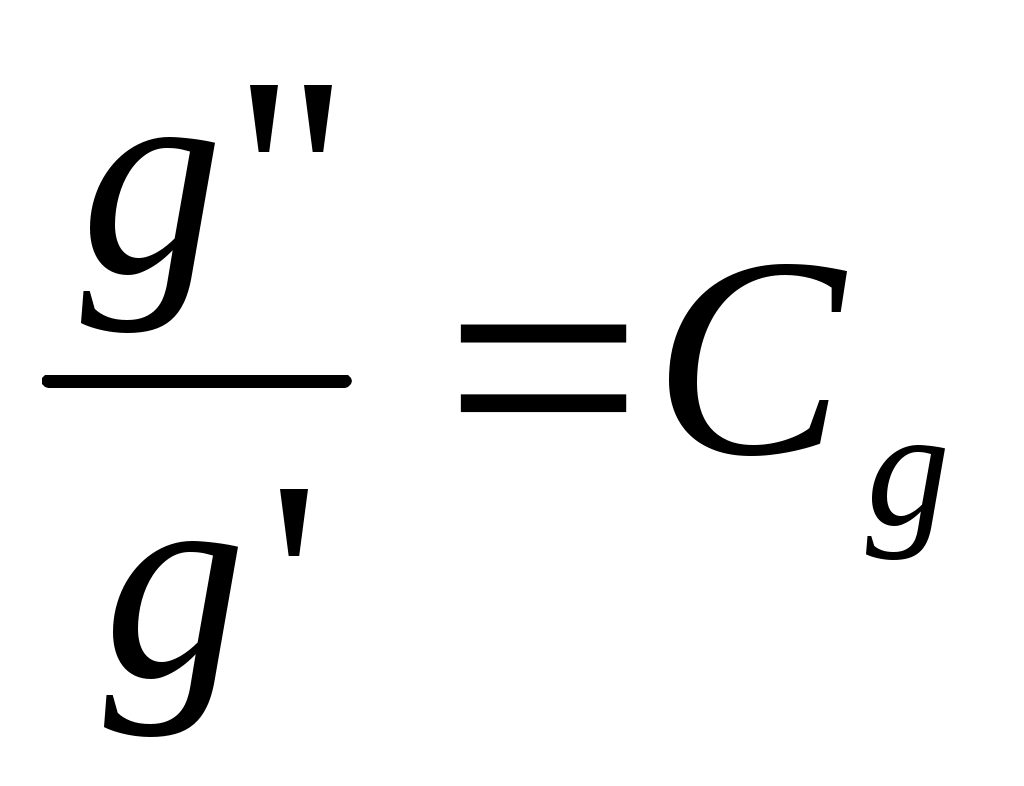 ; ;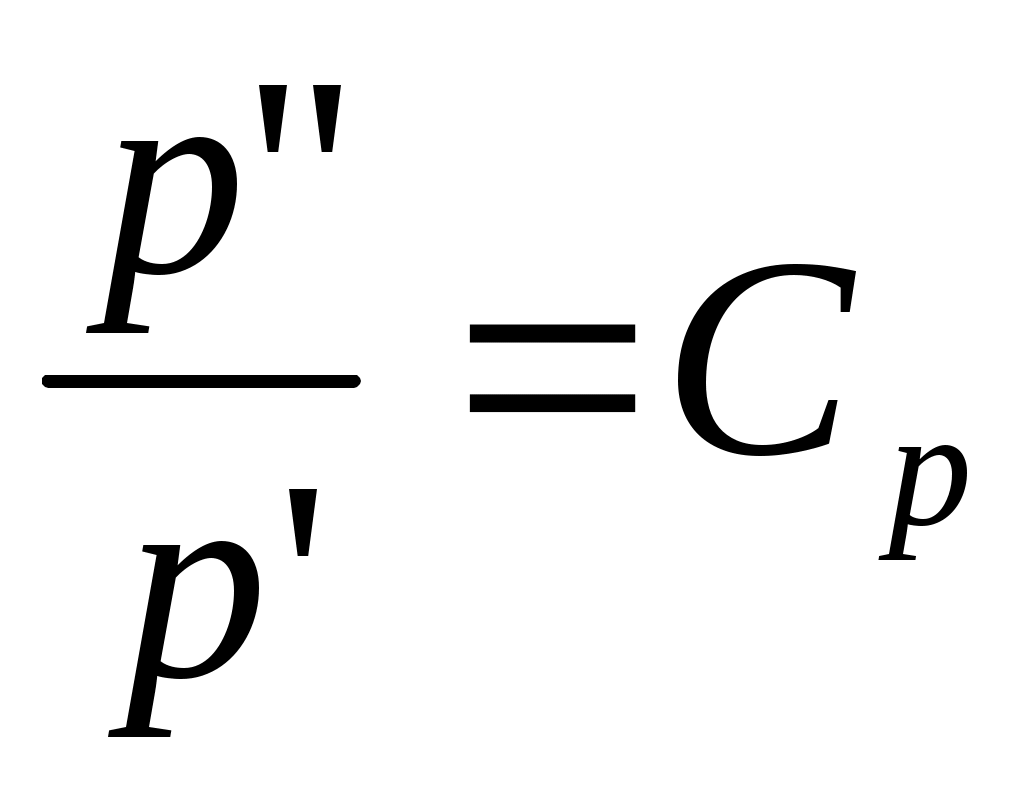 ; ;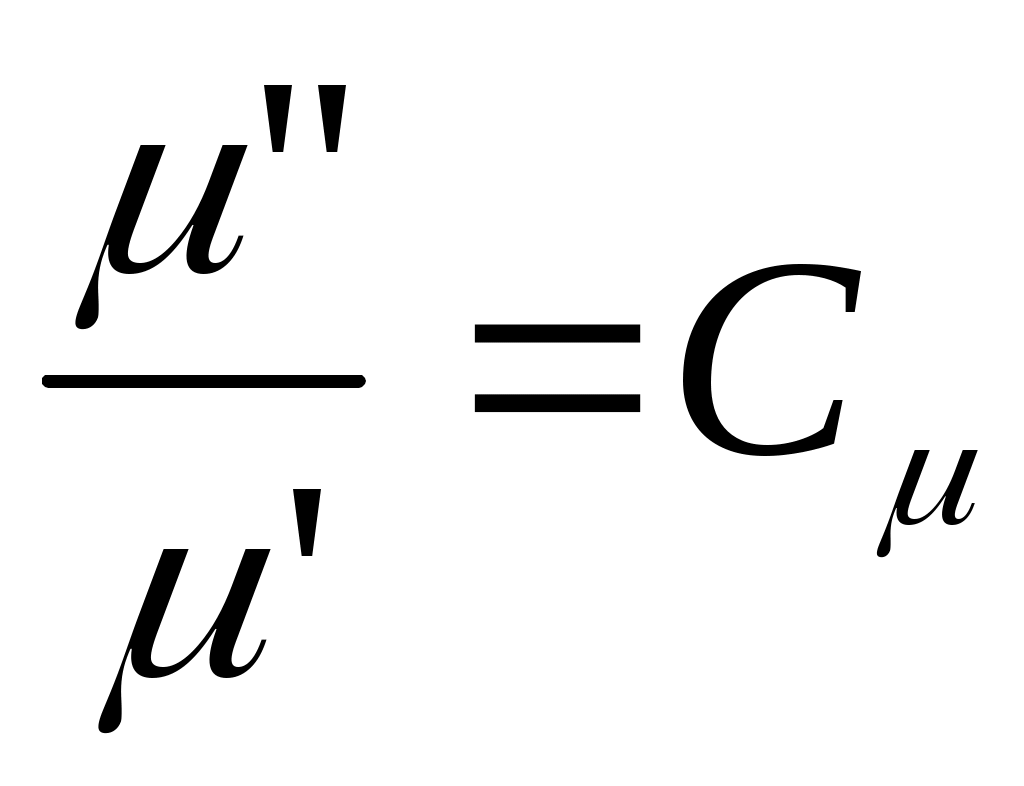 (*) (*)На основании этого мы можем выразить все переменные в уравнении для процесса «”» через переменные первого процесса и константы подобия. Сделаем это и подставим в уравнение процесса «”» 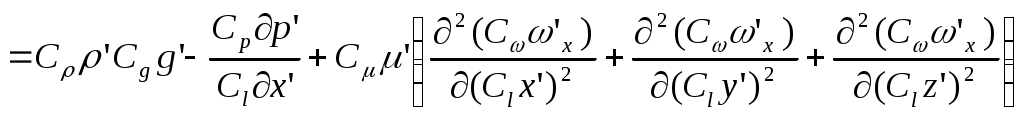 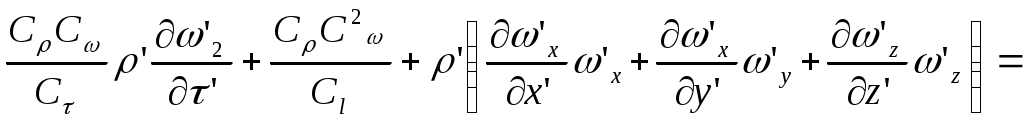 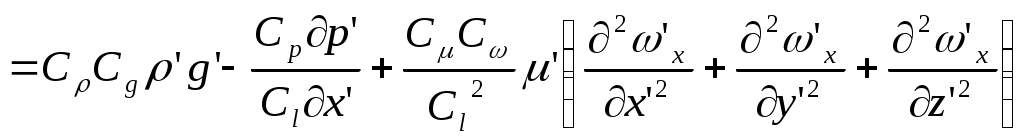 (3) (3)Мы видим, что после сделанных преобразований мы видим, что в уравнение (1) и (3) входят одни и те же переменные. Эти переменные должны определяться одинаково из обоих уравнений (только тогда они будут тождественны). Последнее возможно только в случае если мы сможем сократить в уравнении (3) комплексы (безразмерные) составленные из констант подобия. Для этого должны выполняться неравенства: 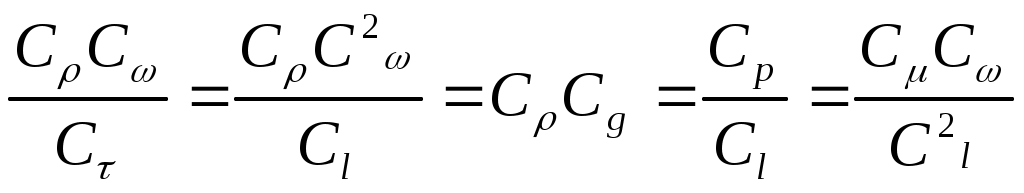 (4) (4)Данное равенство дает нам зависимость между константами гидромеханического подобия. Из него мы видим, что произвольно выбирать все консттанты нельзя. Рассматривая эти комплексы попарно можно получить критериальные числа гидромеханического подобия. Возьмем первые условия: 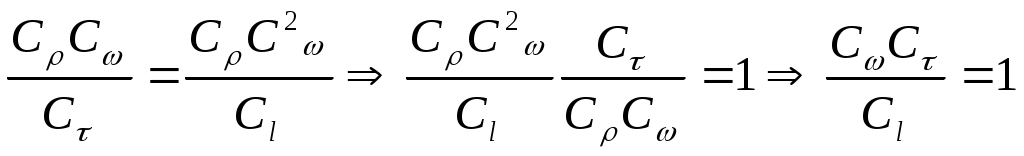 Получим первый индикатор подобия. Для того, чтобы из него получить критериальное число подобия подставляем значение константы подобия из уравнений (*) 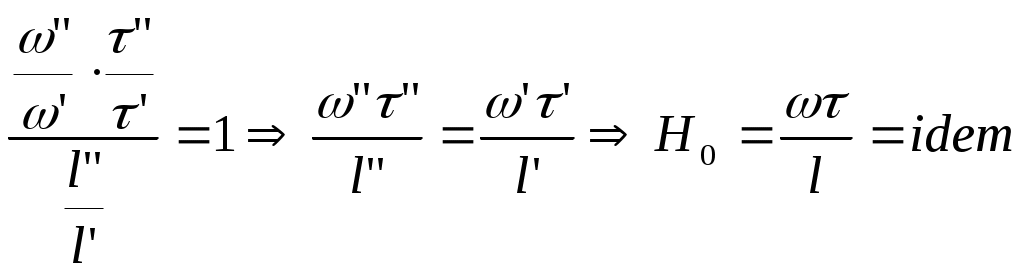 ПолученноеHo- называется число гомохромности, оно характеризует подобие процессов во времени, т.е. применяется для нестационарных процессов. Другими словами можно сказать, что в подобных нестационарных процессах движения жидкости число гомохромности Ho одинаково (согласно 1 – ой теореме подобия). Для подобия стационарных процессов число гомохромности не рассматривается. Рассмотрим вторую пару: 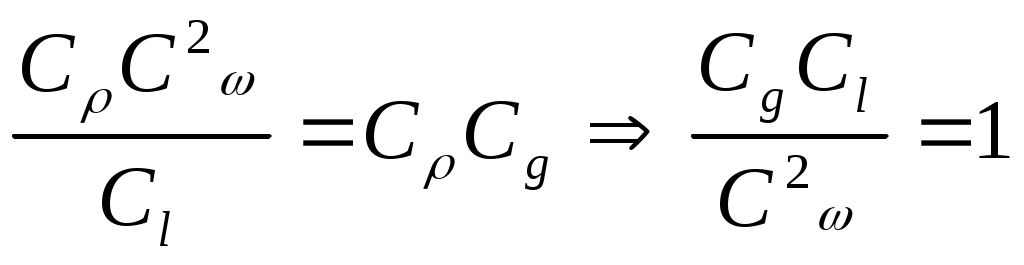 , по аналогии с выводом числа гомохромности подставим в полученный индикатор подобия значение констант из уравнения (*) и окончательно получим: , по аналогии с выводом числа гомохромности подставим в полученный индикатор подобия значение констант из уравнения (*) и окончательно получим: Полученное критериальное число подобия называется Fr – число Фруда, из полученного нами уравнения мы видим. Что число Фрудо является мерой отношения силы тяжести «g» к инерционной силе ω2. Данное число подобия используется при изучении внутреннего движения жидкости. Это число характеризует подобие силовых полей. Теперь рассмотрим третью пару: 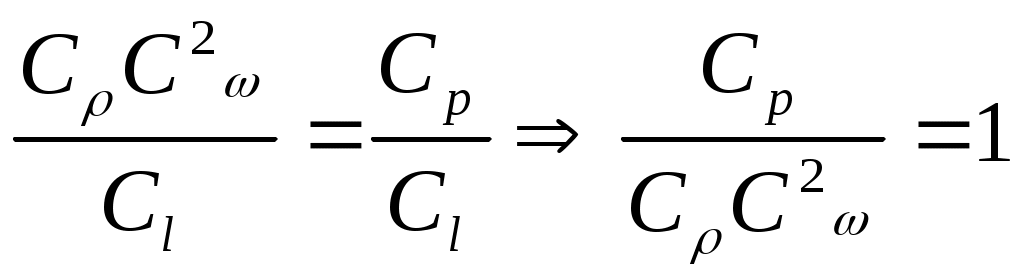 подставляет в данный индикатор подобия значение констант подобия из уравнений (*) получим: подставляет в данный индикатор подобия значение констант подобия из уравнений (*) получим: 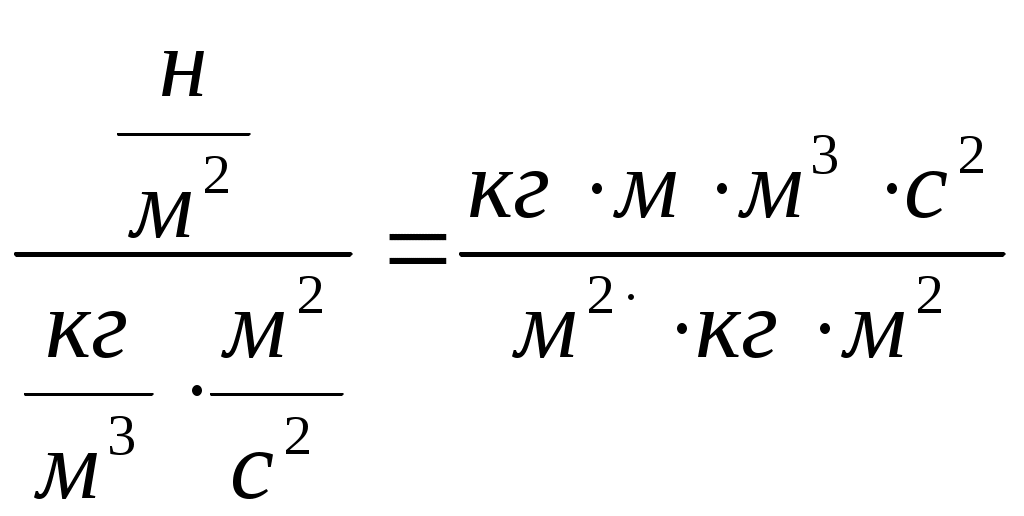 Eu – число Эйлера – является мерой отношения перепада статического давления (гидравлического сопротивления) к динамическому напору потока (скоростной напор). Это число используется при определении гидравлических сопротивлений в потоке. Выведем еще одно важное критериальное число подобия, для чего используем пару: 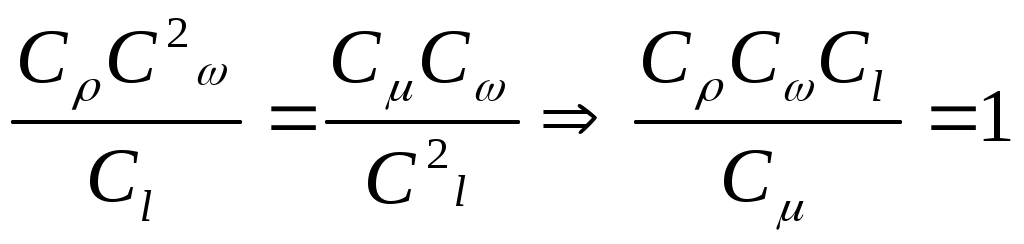 , подставим значения констант подобия и получаем , подставим значения констант подобия и получаем если учесть, что µ/ρ=υ - кинематическая вязкость Re – число Рейнольдца – оно выражает соотношение сил инерции и сил вязкостного внутреннего трения в потоке жидкости. Это число подобия характеризует подобие полей скоростей и режима движения. Таким образом мы можем сказать, что: В гидромеханических подобных системах в любых сходственных точках числа подобия Ho;Fr;Eu и Re имеют одинаковые значения. Это и есть условия гидромеханического подобия. Из полученных нами чисел подобия, числа Ho;Fr;Re являются определяющими – критериальными, а число Эйлера определяемым: Eu=f(H0;Fr;Re) Существует и ряд других чисел гидромеханического подобия: Gr - Грасгофа, Ar – Архимеда, Ga – Галилея. Мы с вами остановимся только на Gr. Почему? Дело в том, что в случае свободного движения жидкости, (естественная конвекция) при рассмотрении силового подобия, вместо числа Фруда удобнее применять число Грасгофа. Это связано с тем, что причиной свободного движения является разность плотностей жидкости и в таком потоке практически невозможно измерить скорости жидкости где β- температурный коэффициент объемного расширения. Gr- число Грасгофа – выражает соотношение между подъёмной силой в жидкости и силами внутреннего трения. Используется при изучении естественной конвекции. 2.5.2 Условия теплового подобия. Тепловое подобие заключается в подобии температурных полей и тепловых потоков. При этом это полагается предварительное обязательное геометрическое и гидромеханическое подобия. Для ввода критериальных чисел теплового подобия воспользуемся уравнением теплообмена и энергии. Для простоты уравнения энергии рассмотрим для одномерного нестационарного случая (сокращение записи). Пусть имеем две подобные системы. Запишем для них уравнение теплообмена и энергии: 1-ая система 2-ая система 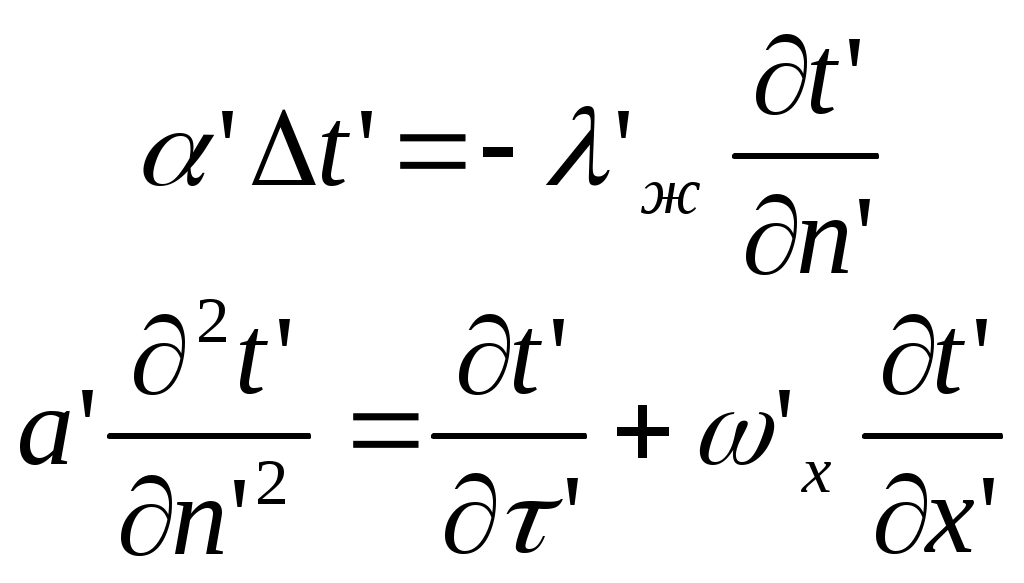 (1) (1) 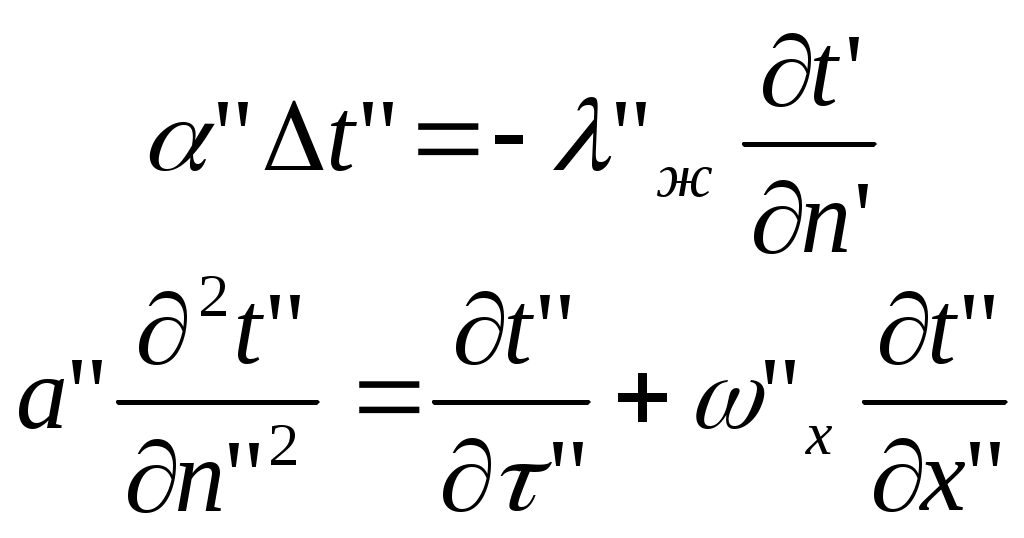 (2) (2)Так как процессы подобны, то для них отношения сходства величин постоянны и равны соответствующим константам подобия 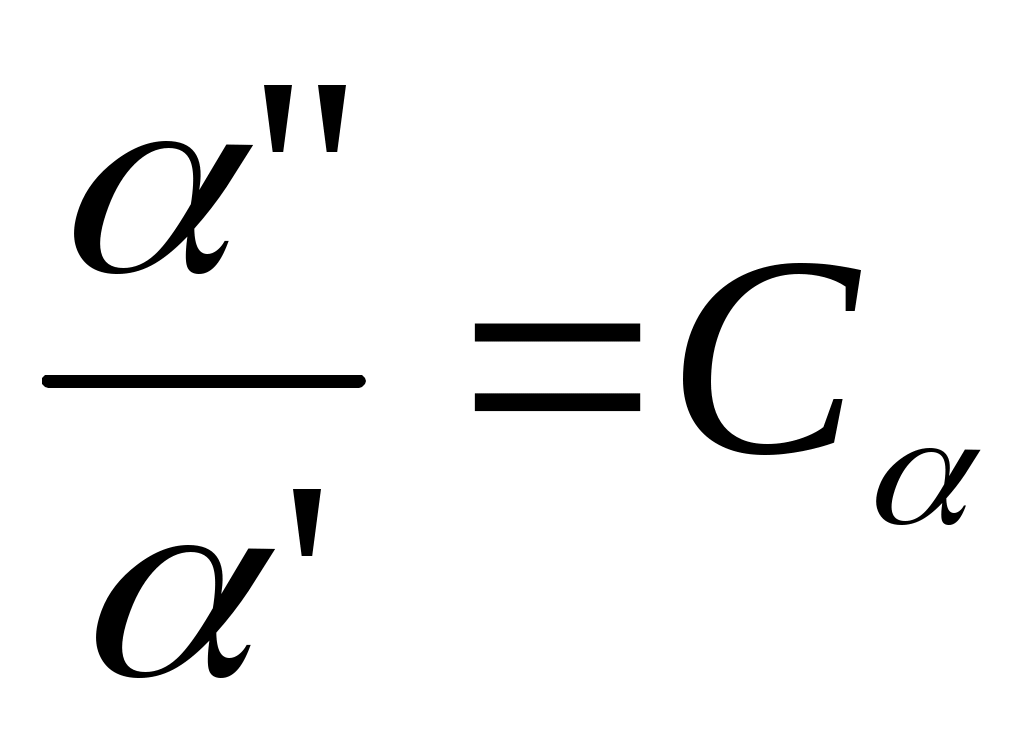 ; ;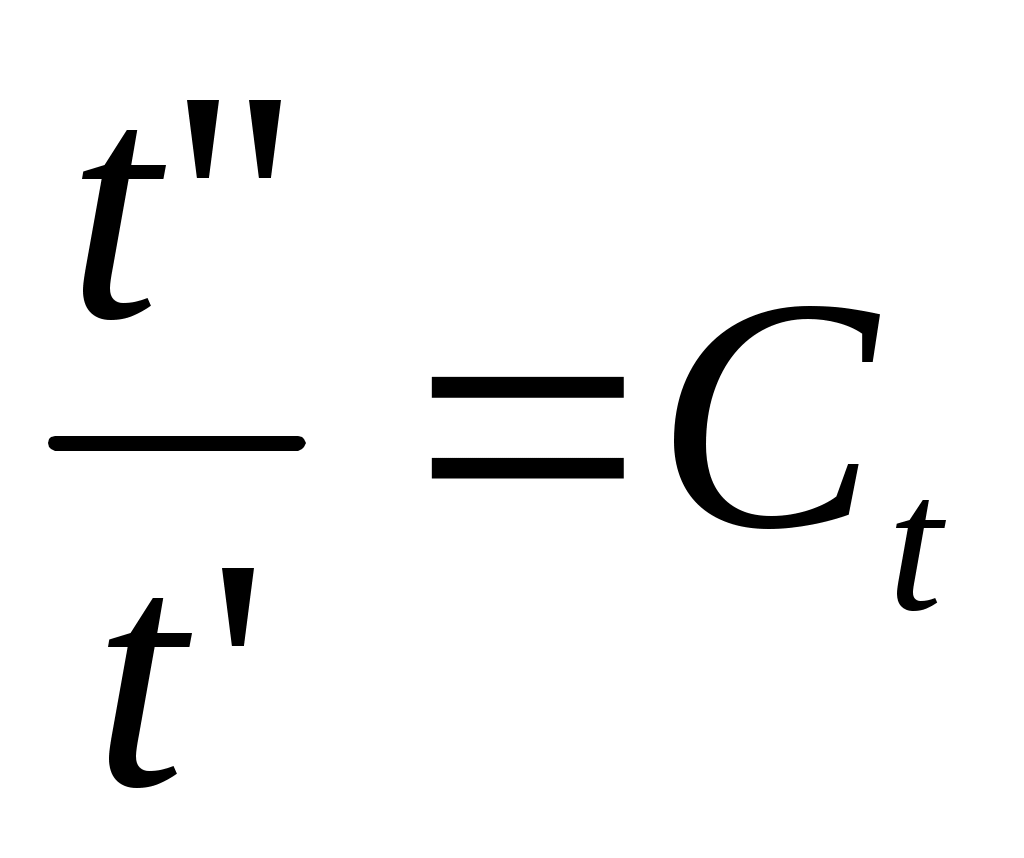 ; ;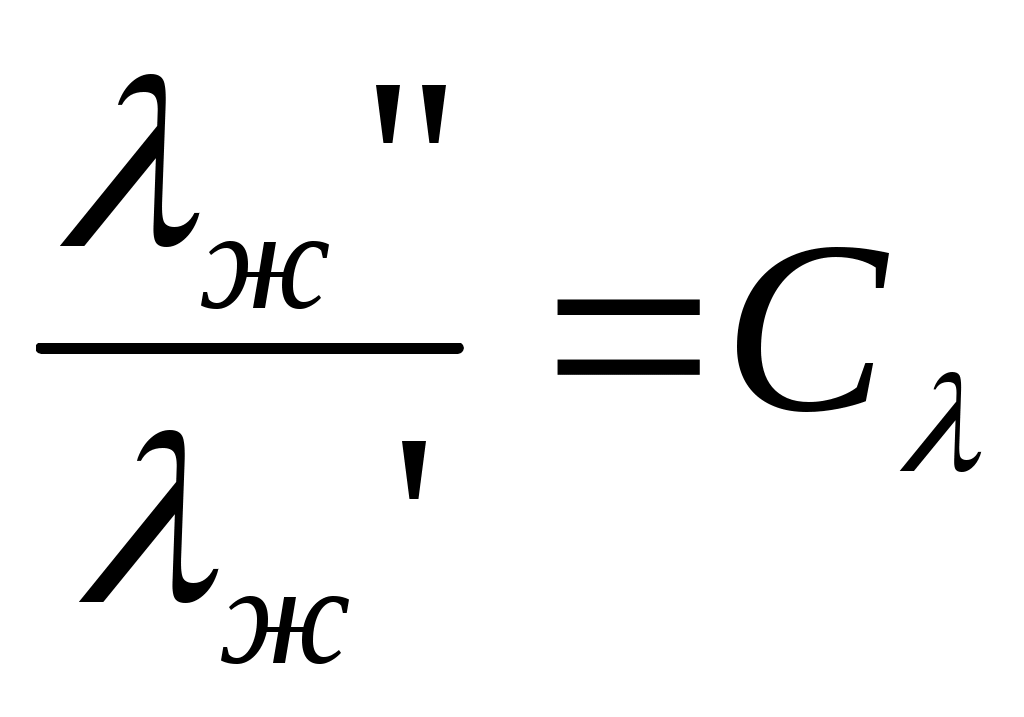 ; ;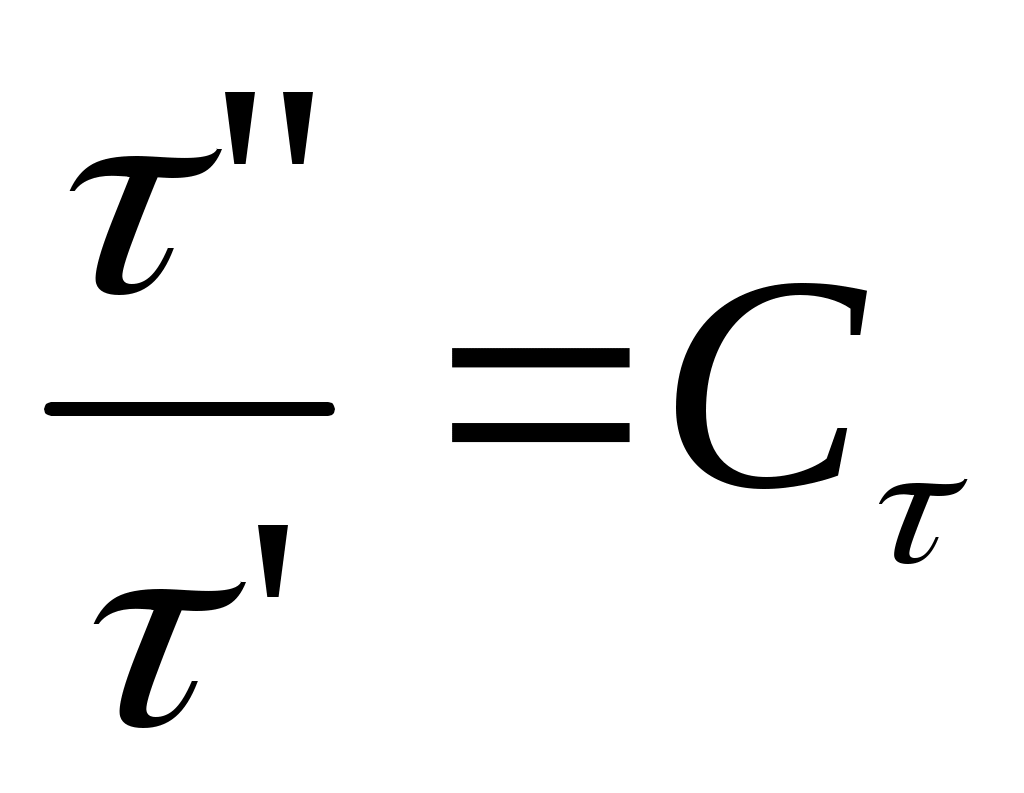 ; ;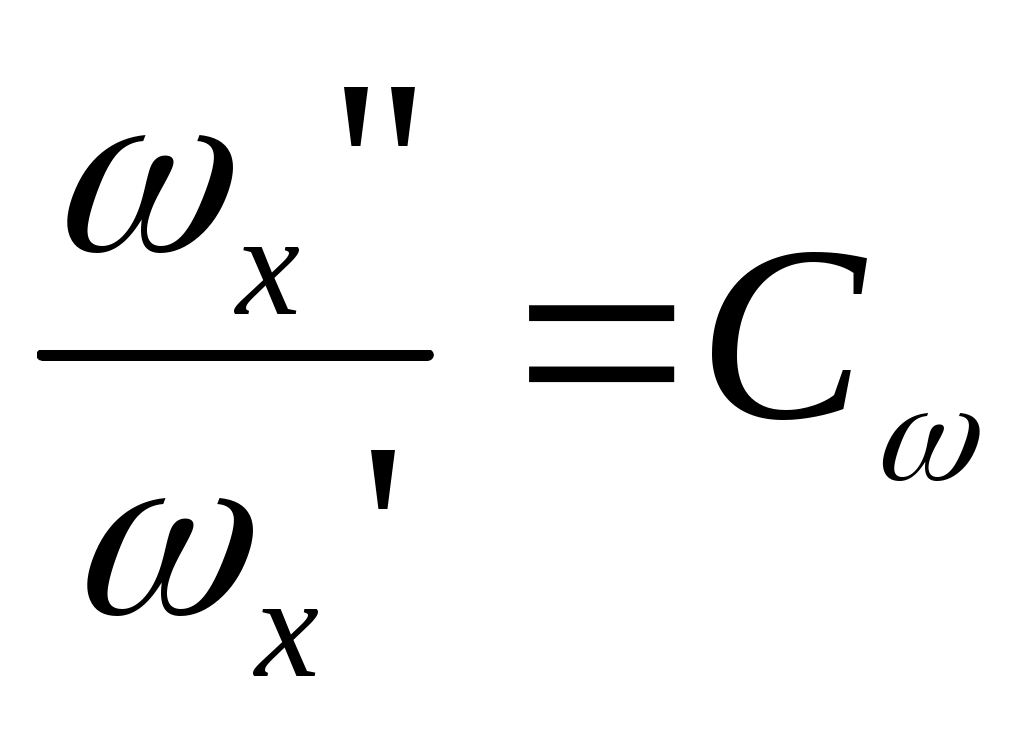 ; ;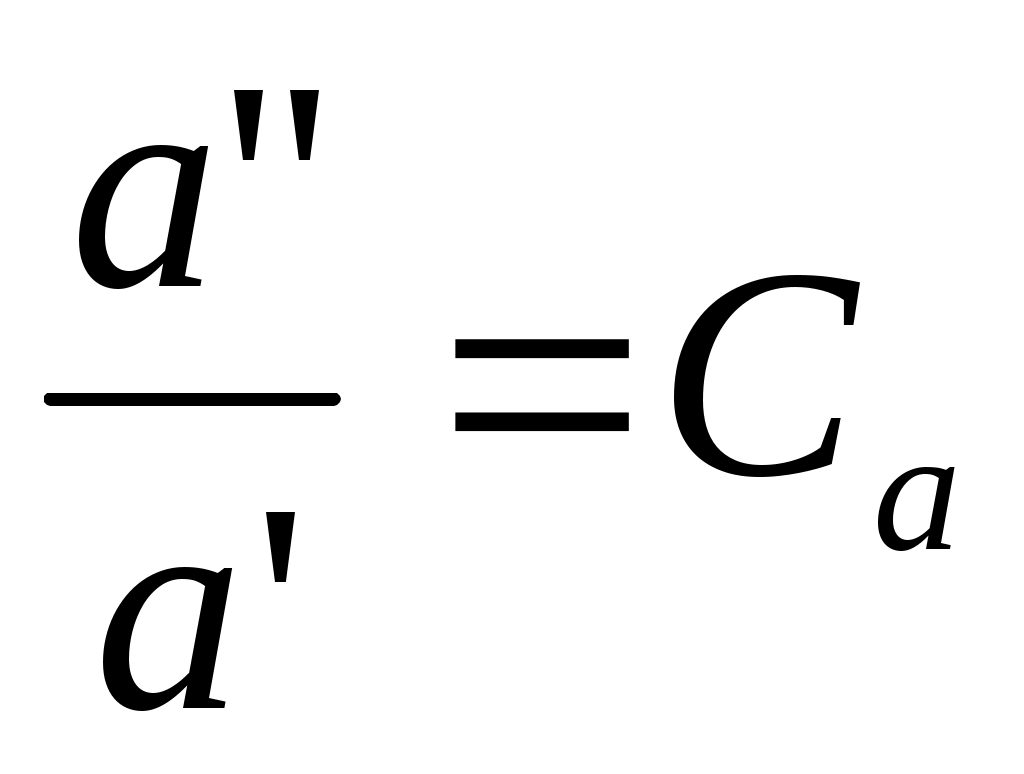 (*) (*)Выразим, как и в случае вывода чисел гидромеханического подобия, все переменные в уравнении (2) через переменные уравнений (1) с помощью соотношений (*). Я буду выражать и сразу группировать, что бы было меньше писанины. 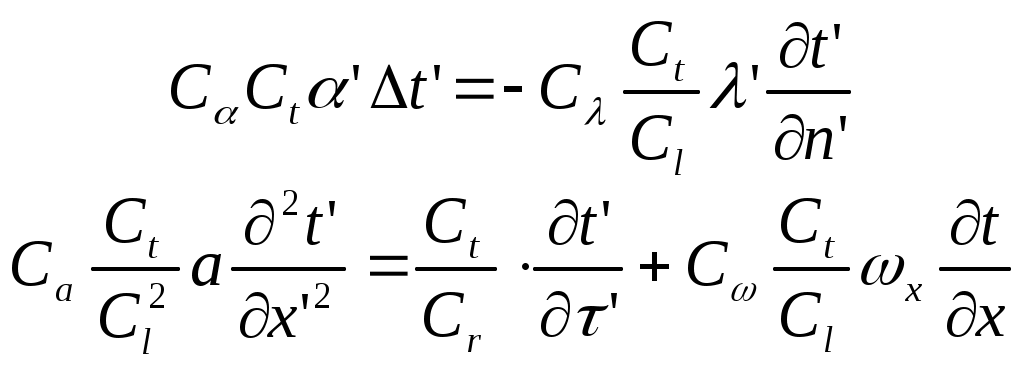 (3) (3)Мы видим, что уравнение (1) и (3) состоит из одинаковых переменных. Которые должны из них определяться одинаково. Поэтому в уравнениях (3) должны сокращаться безразмерные комплексы состоящие из констант подобия. Итак мы получим соотношения между константами теплового подобия. Рассматривая эти комплексы попарно можно получить числа теплового подобия. Из условия: 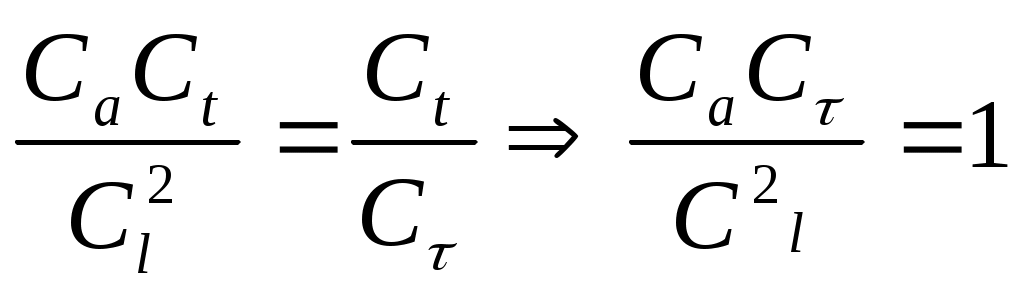 , для получения из полученного индикатора подобия числа теплового подобия подставим в него значения констант подобия из уравнений (*) , для получения из полученного индикатора подобия числа теплового подобия подставим в него значения констант подобия из уравнений (*)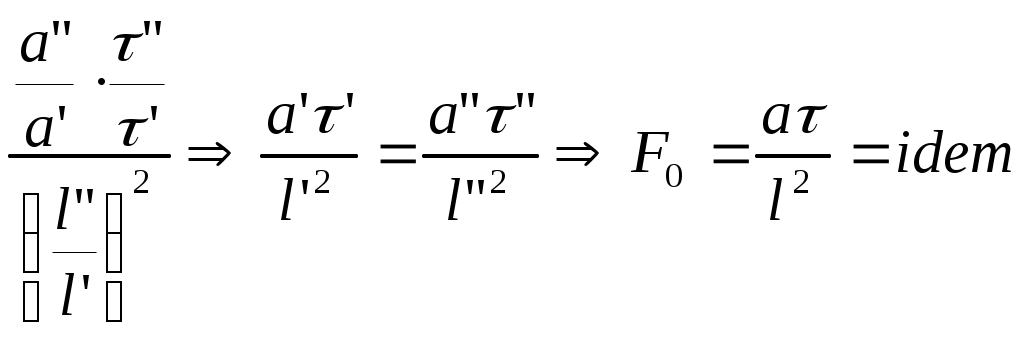 F0– число Фурье – оно характеризует не стационарность тепловых процессов и выражает соотношение между скоростью изменения температурного поля, размерами и физическими свойствами тела. Чем выше F0 – тем скорее греется тело. Из условия: 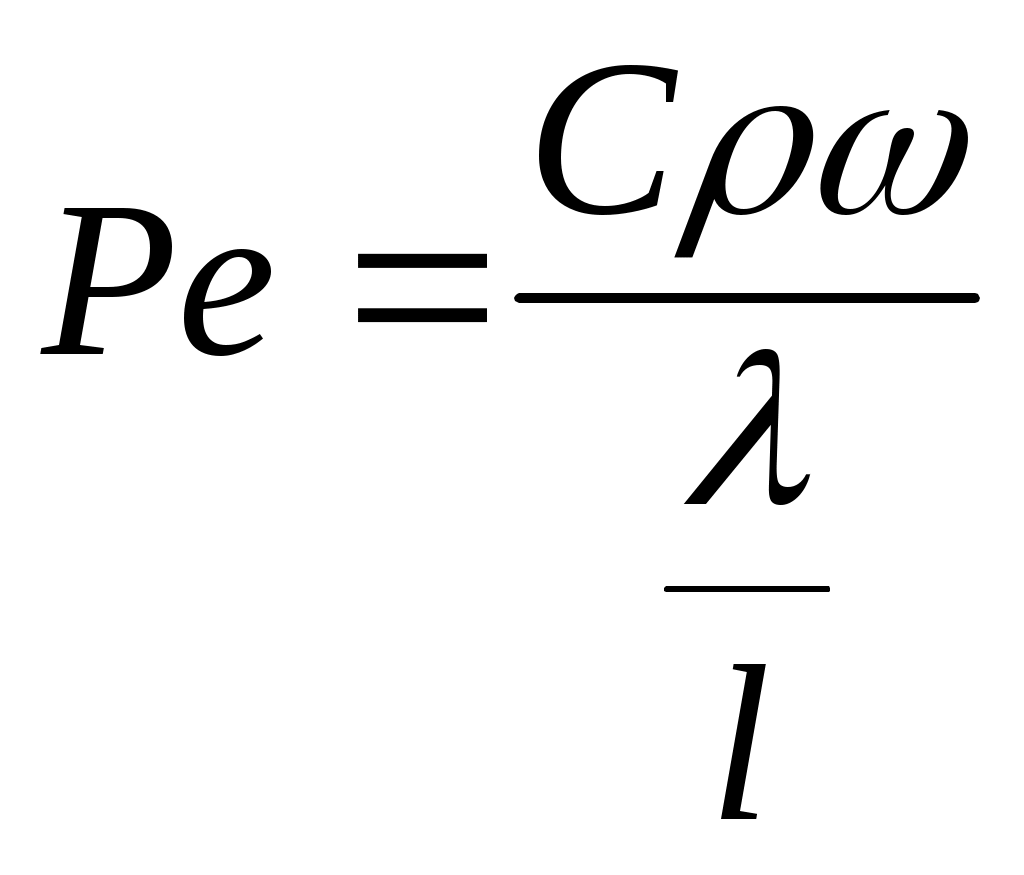 Pe – число Пекле – оно характеризует соотношение между переносом теплоты конвекцией Если в изучаемых системах температурное поле подобны, то для них Из условия: Nu– число Нуссельта – оно характеризует интенсивность теплообмена на границе раздела жидкости и твердого тела, т. е. интенсивность теплоотдачи. Это безразмерный коэффициент теплоотдачи. Число Нуссельта является определяемым, т.к. в его состав входит искомый коэффициент теплоотдачи “ Теперь мы можем сформулировать и условия теплового подобия. При тепловом подобии систем в любых сходственных точках и сходственные моменты времени числа подобия Fo, Pe и Nuдолжны иметь одинаковые значения: Nu=f(F0;Pe) Введем еще одно важное число подобия. Если мы с вами посмотрим на числа Pr – число Прандтля – оно состоит только из физических свойств жидкости и само является физическим свойством. Зависит только от рода жидкости и её состояния. Оно представляет собой соотношение между гидродинамическим и тепловым пограничными слоями. Для идеальных газов Pr – от 0,66 – 1 не зависит от температуры и давления. Для жидкостей Prбольше 1 и является функцией температуры. Для жидких металлов Pr много меньше 1. 2.6 Уравнение подобия конвективного теплообмена При изучении процессов конвективного теплообмена основной определяемой величиной является коэффициент теплоотдачи α=f(ω;tc;tж;λ;ρ;Cp;α;β;µ;l1;l2;…;Ф) Определение В соответствии с второй теоремой подобия критерии, определяемые из системы дифференциальных уравнений, описываются и критериями. получаемыми из уравнений являющихся решение дифференциальных уравнений. Поэтому на основании полученных нами чисел подобия мы можем составить уравнение подобия конвективного теплообмена, решая которые, можно найти α(α входит в Nu). В наиболее общем виде оно запишется так: Nu=f(H0;Gr;Re;F0;Pe;l/l0) (1) Как вы видите, уравнение подобия, на ряду с числами подобия, входит симплекс подобия l/l0 Входящие сюда числа Гомохромности Ho;Fo Фурье характеризуют не стационарность процессов. Однако, наибольший интерес для практики представляет определение α в установившемся, т.е стационарном режиме Nu=f(Gr;Re;Pe;l/lo) (2) или учитываем, что Pe=Re∙Pr имеем Nu=f(Gr;Re;Pr;l/lo) (2а) В некоторых случаях уравнение подобия конвективного теплообмена может еще более упроститься. Например, при вынужденном турбулентном движении. Когда движение идет за счет работы насоса или вентилятора. Можно пренебречь влиянием на конвективный теплообмен числа Грасгофа , характеризующего свободную конвекцию (за счет разности ρ). Тогда уравнение подобия примет вид: Nu=f(Re;Pr;l/lo) (3) Для газов, для которых Pr=const , уравнение подобия вынужденного движения еще более упрощается Nu=f(Re;l/lo) (3а) При свободном движении, когда отсутствует вынужденная конвекция (нет насосов и вентиляторов) уравнение (2а) можно пренебречь числом Re : Nu=f(Gr;Pr;l/lo) (4) Условия подобия процессов получены в предположении, что физические характеристики теплоносителя (Cp;λ;υ) постоянны во всей области протекания процесса. В действительности они зависят от температуры, и эта зависимость для разных теплоносителей различна. Подобие процессов выполняется тем полнее. Чем меньше относительное изменение этих свойств в функции от температуры. В заключении подчеркну, что использование уравнения подобия конвективного теплообмена позволяет заменить изучение процессов в натурных объектах изучением их на моделях (дешевле, а иногда в натуре не возможно; меньше ошибок при проектировании). Остается не выясненным последний вопрос, а как же получить конкретный вид уравнения подобия для различных случаев теплоотдачи? А для этого необходимо проведение ряда экспериментальных работ и обобщения их результатов. |
