Лекции по теплопередачи (Конвективный теплообмен, Word). 2. конвективный теплообмен основные понятия и определения

• Название: 2. конвективный теплообмен основные понятия и определения
• Дата: 04.11.2022
• Размер: 1.22 Mb.
• Имя файла: Лекции по теплопередачи (Конвективный теплообмен, Word).doc
• Тип: Документы; #770565
• страница: 4 из 7

2.5 Обработка и обобщение результатов экспериментального исследования процессов теплоотдачи.
Главной задачей экспериментального изучении процесса конвективного теплообмена является определение коэффициента теплоотдачи и установления конкретного вида уравнения подобия, чтобы в дальнейшем с его помощью исследовать целый класс процессов подобных данному (исследованием на модели, а перешли на натуру)

Наиболее распространенным методом определения α является метод стационарного потока. При нем α определяется из уравнения Ньютона - Рихмана:

(1)

где Q – тепловой поток ;

t_cт- температура стенки ;

t_ж - температура потока жидкости ;

F– площадь поверхности теплообмена ;

Мы видим, что для определения из опыта нам необходимо измерить Q; t_cт;t_ж;F.

Методы определения теплового потока Q зависит от способа организации подвода теплоты. Он выбирается экспериментатором. В зависимости от исследуемого процесса (свободная конвекция – греющая труба; вынужденная - пылесос гонит воздух или насос - воду).

1)Наиболее простой способ это нагрев поверхности теплообмена электрическим потоком. В этом случае тепловой поток Q определяется по замеренным в опыте силе тока I и падение напряжения

Q=I∆U (как видели на л.р.)

2)При исследовании теплообмена жидкостей в трубах и других каналах измерить подводимую (отводимую) теплоту можно определить изменению энтальпий (dI=C_pdT). В этом случае тепловой поток определяется из уравнения теплового баланса:



где G – массовый расход жидкости,

- средняя удельная изобарная теплоемкость жидкости

t’_ж и t”_ж- температура жидкости на входе и на выходе.

Существует ряд других способов отвода и подвода теплоты и определения Q. При необходимости вы их всегда найдете в специальной литературе.

Некоторые сложности возникают при измерении температур. Встает вопрос, какие температуры подставлять в расчетные уравнения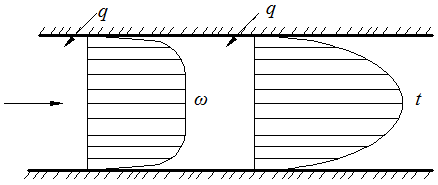


При движении жидкости в канале и наличие теплообмена (например подвод тепла) температура жидкости в различных точках канала будет различной (она меняется как по длине канала, так и по его сечению. Аналогично можем изменять и скорость потока.)

В технических расчетах, как правило фигурирует понятие средней скорости и средней температуры. Для их определения существуют специальные способы усреднения. Поэтому необходимо усреднять замеренные температуры по длине канала и по его сечению.

а) Усреднение по сечению

Пусть мы имеем полученные экспериментально распределение ω и t по сечению произвольного канала (смотри рисунок). Т.к. ω и t не постоянны, то через элементарные сечения dfв разных точках будет проходить разное количество жидкости ρωdf и имеющей разную энтальпию C_pρωdf. Тогда среднюю по сечению температуру можно получить так: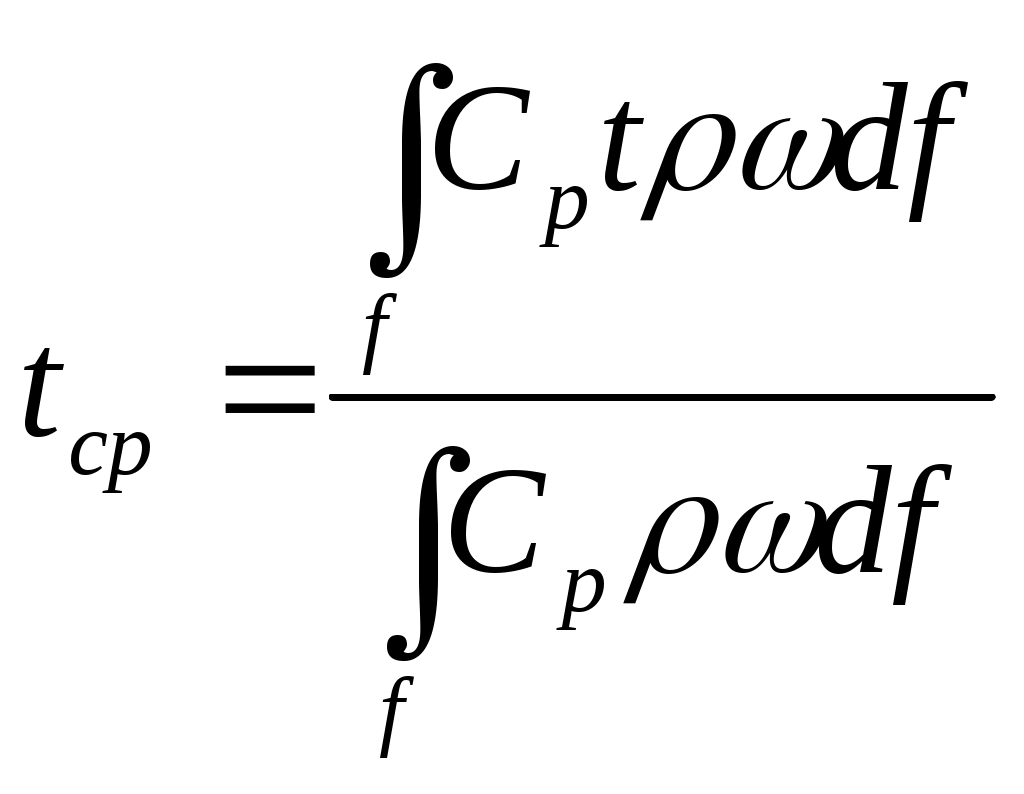

;

Числитель - энтальпия массового расхода через сечение df



Знаменатель – теплоемкость (полная) этого же расхода.

По этой формуле всегда можно определить среднюю по сечению температуру жидкости. Если C_pиρ в сечении не зависят от температуры, то формула принимает вид: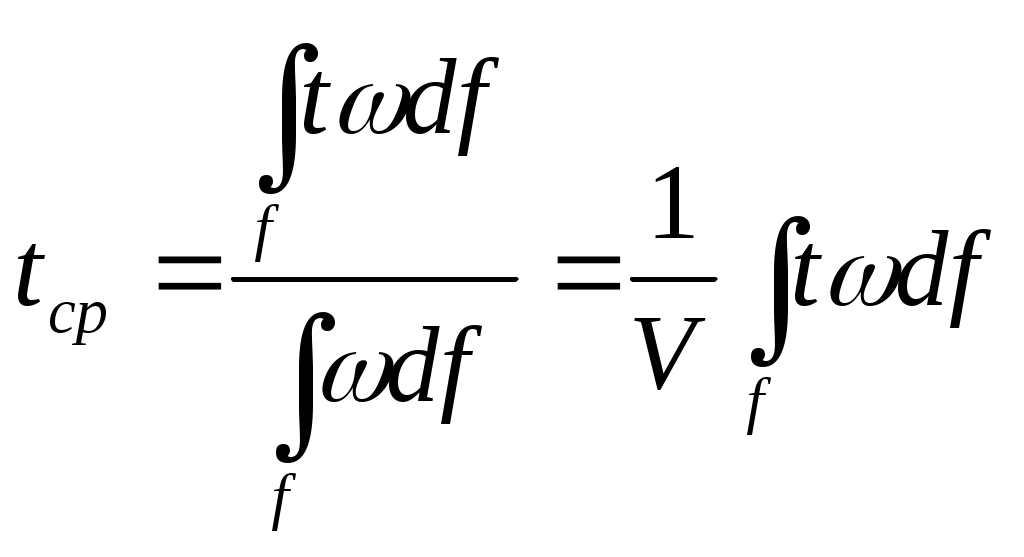
,

V – объемный расход

Средняя скорость по сечению определяется так:



V – объемный расход;

f – площадь сечения.

Иногда среднюю по сечению температуру потока определяют экспериментально. Для этого в канале, перед местом измерения температуры ставятся перемешивающее устройство. После него температура по сечению выравнивается, и становиться средней по энтальпии. Эту температуру называют температурой смешения. Понятно, что такое измерение сопряжено с существенными гидравлическими потерями.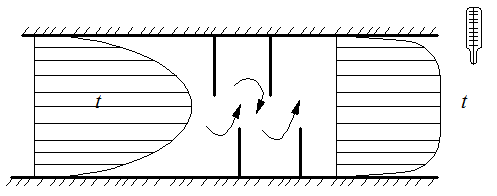



б) Усреднение по длине канала

Как мы отметили при движении жидкости её температура меняется не только по сечению канала, но и по его длине.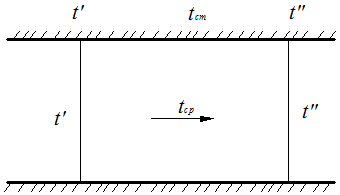



В общем случае усреднение производиться по следующей формуле:


где t_cт - температура стенки определяемая как среднеарифметическая по опытным данным;

“+” – охлаждение жидкости;

“-” – нагрев жидкости;

- сределогарифмическая разность температур жидкости и твердой стенки по всему каналу.

;

где ;

В том случае, когда изменение температуры по длине канала незначительно, средняя температура её может быть взята как среднеарифметическое: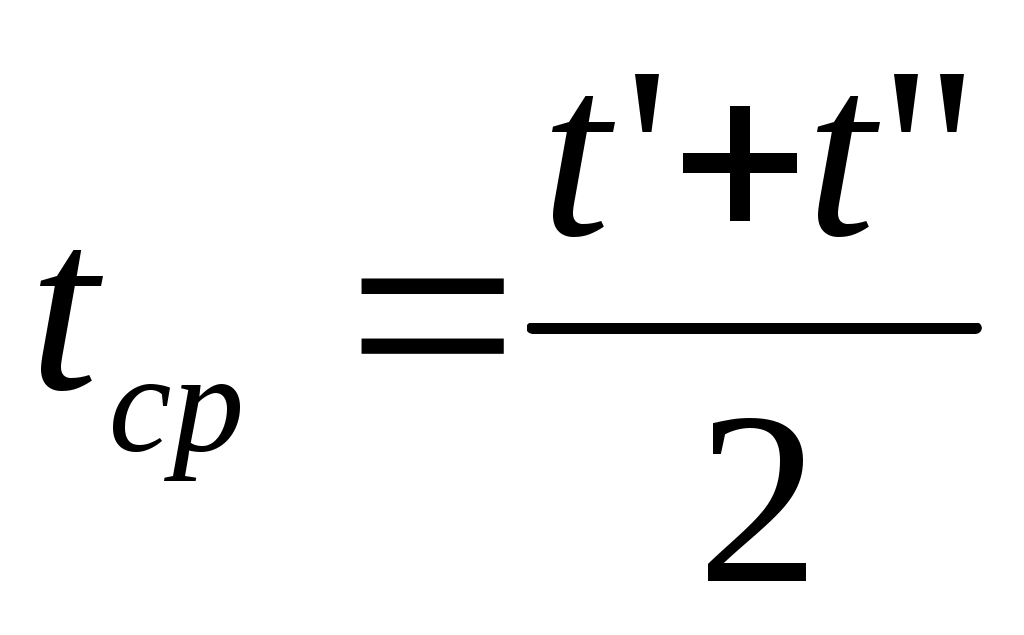

В общем случае когда 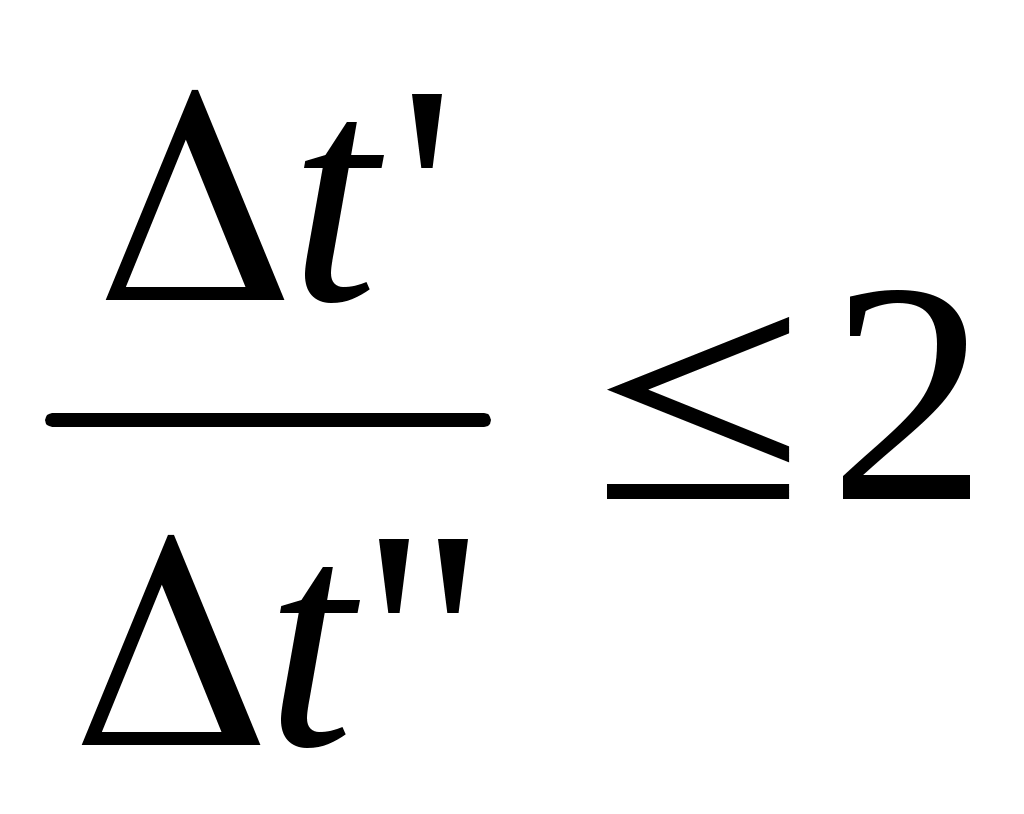без существенной погрешности средняя температура по каналу может быть определена как среднеарифметическая.

В дальнейшем во всех наших уравнениях будут фигурировать только средние температуры и скорости, поэтому индекс «ср» мы будем опускать.

Т.к. в процессе теплоотдачи изменяется температура жидкости, то одновременно с этим меняются её физические свойства λ,C_p… Возникает проблема усреднения физических свойств в жидкости при исследовании теплообмена.

Усреднение физических свойств в жидкости осуществляется по определяющей температуре, т.е. той температуре, по которой они берутся из справочника. Эта температура выбирается достаточно произвольно. Очень часто за неё принимают среднюю температуру потока жидкости, а иногда и стенки.

Надо отметить, что выбор определяющей температуры и по ним физических параметров приводиться к тому, что на базе одних и тех же опытов принимаем разную определяющую температуру t (t_ж;t_cт) разные исследователи получают различные формулы. В связи с этим у физических параметров и чисел подобия проставляется индекс указывающий по какой определяющей температуре они брались: Re_ж;Pr_ж;Pr_ст;λ_ст;λ_ж…

Теперь, измерив и определив все необходимые параметры процесса теплоотдачи в опыте, для того чтобы их можно было распространить на подобные процессы, согласно второй теореме подобия их обработку надо производить в критериях подобия.

Т.е. теперь по опытным данным мы должны вычислить все критерии подобия и составить зависимость между ними.

Обычно, при обработке опытных данных уравнения подобия представляются в виде степенных функций, например:



где С,n,m – некоторые константы, которые необходимо определить при обработке опытных данных.

Для этого пользуются логарифмическим масштабом. Почему? Это связано с тем, что в степенных уравнениях в логарифмических координатах они изображаются прямыми линиями.

Например, для экономии времени рассмотрим уравнение в виде:



В логарифмических координатах, оно примет вид:

lnNu=lnC+nlnRe

По опытным данным мы можем посчитать числа Nu(α) и Re(ω) и по этим значения построим график.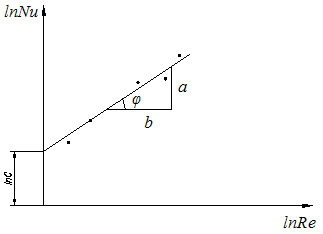



Если нарисуем то видно, что

Переменную С можно так же снять с графика или определить непосредственно из уравнения:



Иногда, в следствии погрешности измерения, точки с координатами (Nu;Re) не укладываются на одну прямую. В этом случае строится осреднённая прямая.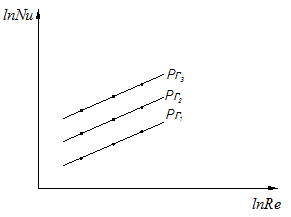



При рассмотрении уравнения типа Nu=CReⁿPr^m в логарифмических координатах будет серия прямых, каждая из которых соответствует определенному числу Pr. По этому графику можно определить показатель степени числа Re. Показатель степени «m» у числа Pr находиться из дополнительного графика, который строится в координатах . Определение производиться аналогично рассмотренному нами случаю.

Ну еще об одном параметре. В ряд чисел подобия входит линейная величинаl.

эту величину называют определяющим линейным размером. За него принимают тот размер. Который в наибольшей степени влияет на теплоотдачу. Все остальные линейные размеры в уравнении подобия входят в виде симплексов .

Этот размер берется для разных случаев по разному. Например при поперечном омывании пучка труб (радиатор) в качестве «l» выбирают наружный диаметр трубы. При исследовании течения жидкости в трубах – внутренний диаметр. Для произвольной формы канала берут эквивалентный диаметр , F – площадь сечения канала, П- периметр
2.7 Теплоотдача при вынужденном движении теплоносителя.
Мы с вами отметили, что процесс теплоотдачи зависит от природы возникновения течения жидкости. При этом различают вынужденное (вызываемое вентиляторами, насосами и другими возбудителями). Начнем с вынужденного движения наиболее часто встречающейся в технике случае. Это движение жидкости в каналах различной формы и омывания потоком жидкости пучка труб.
2.7.1 Теплоотдача при вынужденном движении жидкости в каналах.
При вынужденном движении жидкости теплоотдача в основном определяется режимом движения. По характеру движения жидкости различают два основных режима жидкости: ламинарный (слоистый) и турбулентный (вихревой). Ламинарный режим наблюдается при малых скоростях, турбулентный при больших, т. е. можно сделать вывод что режим движения зависит от скорости 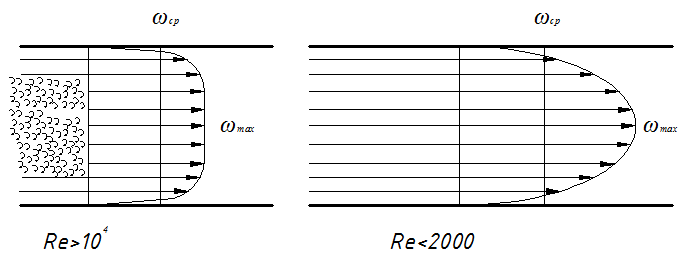. Переход режима движения из ламинарного в турбулентный переходит как только скорость движения достигает критической, причем значение этой критической скорости различно, для различной жидкости.



Рейнольдс установил, что переход жидкости от ламинарного течения к турбулентному обусловлен значение безразмерного комплекса



Опытом он установил, что для любой жидкости при Re <2000 наблюдается ламинарный режим. При переходный режим. При Re>10⁴ развитое турбулентное движение.

Исходя из значения числа Reможно определить значение для критической скорости любой жидкости



Между ламинарным и турбулентном движении жидкости в трубах помимо качественного имеется еще и количественное различия, показывающие существенное влияние на теплоотдачу. Оно заключается в различных законах изменения скоростей по сечению трубы: параболическое при ламинарном и более крутое у стенок и равномерное в ядре потока при турбулентном. Соответствен имеют разные значения отношения средней скорости по сечению к его максимальному значению:

ламинарный:

турбулентный:

Наличие этого участка обусловлено действием сил вязкостного трения.

Такие законы распределения скоростей характерны только для гидродинамически стабильного течения. Стабилизация наступает не сразу, а на некотором расстоянии l_н от входа в трубу. Если в трубу с закругленными кромками жидкость поступает из большого пространства, то на входе скорость постоянна. Далее, в следствии трения у стенки скорость убывает, а в центре потока растет. Так постепенно изменяясь на участке стабилизации эпюра скоростей принимает стабильный вид:

l_н ≈40d- при турбулентном режиме.

l_н ≈0,03∙Re- при ламинарном режиме.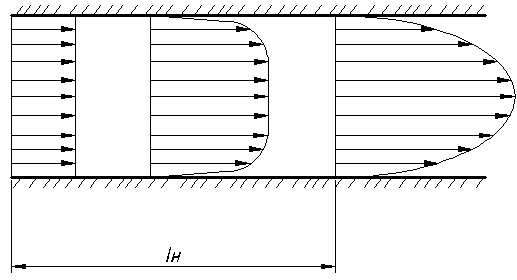



Так как на участке гидромеханической стабилизации характер движения жидкости меняется, то меняется теплоотдача. Поэтому при проведении исследований следует указывать имеет ли место гидромеханическая стабилизация или нет. В противном случае возможны ошибки.

При турбулентном режиме движения жидкости у стенки всегда имеется небольшой слой, в котором жидкость движется ламинарно. Это ламинарный пограничный слой. На участке гидромеханической стабилизации толщина этого пограничного слоя изменяется от δ=0на входе в трубу, до своего предельного значения. По своему абсолютному значению величина δ не велика и зависит от числа Re:



При нагреве или охлаждении жидкости в канале, по опытным данным, одновременно с гидродинамической стабилизацией проходит тепловая стабилизация. Она имеет место как при турбулентном, так и при ламинарном режиме.

На участке тепловой стабилизации проходит развитие теплового пограничного слоя.

На входе в трубу ядро потока в теплообмене не участвует и все тепловые изменения проходят только в пограничном тепловом слое.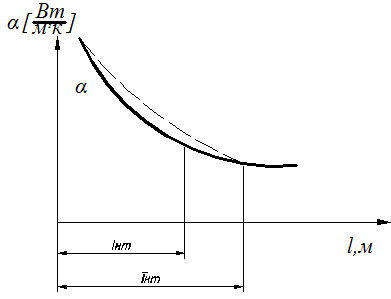


При этом чем меньше толщина этого теплового пограничного слоя, тем интенсивнее протекает теплопередача. Это объясняет тот факт, что на входе в трубу α имеет максимальное значение.

По мере удаления от входа толщина пограничного теплового слоя увеличивается и на некотором расстоянии от входа (l_нт) он занимает всё поперечное сечение канала (т.е. в теплоотдаче уже участвует вся жидкость). Это означает наступление тепловой стабилизации. Коэффициент теплоотдачи на этом участке резко уменьшается стремясь к определенному неизменному значению. После наступления тепловой стабилизации он является постоянным по всей трубе.

Наличие участка тепловой стабилизации жидкости обуславливается низким значением коэффициента теплопроводности жидкости (в начале трубы течение ламинарное, а в нём теплота передается от слоя к слою теплопроводностью) и как следствие этого медленным выравниваем температурного поля.

Аналогично ведет себя и средний по длине канала коэффициент теплопроводности однако стабилизация по нему распространяется на большую длину.

Очевидно, что длинна участка тепловой стабилизации (l_нт) зависит от коэффициента теплопроводности жидкости, диаметра трубы и её положения ((горизонтальная или вертикальная), режима движения и гидродинамической стабилизации).

l_нт=f(λ;d;Re;l_н;Ф) Ф- форма и положение трубы.

Например для горизонтальных труб для определения длины участка тепловой стабилизации справедлива формула l_н.т.=(0,05…0,07)Red_вн, которая для турбулентного режима упрощается и принимает вид l_н.т.=(10…15)d_вн. Влияние же стабилизации на распространяется на участок до 50d_вн.

Характер распределения температурного поля по сечению канала зависит от поля скоростей жидкости и примерного подобия ему. Т.е. при ламинарном течении температура меняется по закону параболы плавно, а при турбулентном режиме температура изменяется в пристенном слое и остается const в ядре потока.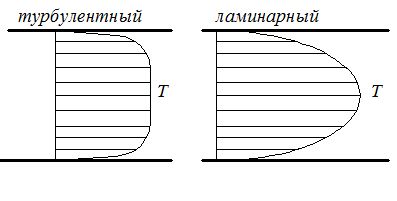



Два основных режима течения жидкости: ламинарный и турбулентный характеризуются и различными механизмами (способами) передачи теплоты при них.

При ламинарном движении (слоистом) теплообмен происходит в основном за счет теплопроводности и лишь частично за счёт свободного движения жидкости поперек канала, в следствии разности температуры жидкости и степени (свободная конвекция). Учитывая малый коэффициент теплопроводности λ можно сделать вывод о малой интенсивности теплопередачи (малом α) при ламинарном режиме движения. (теплота передается теплопроводностью через весь слой жидкости от ядра к стенке)

При турбулентном режиме (вихревом) теплообмен происходит в основном за счёт внутренней конвекции (вихрей в жидкости). Влияние свободного движения полностью исчезает. Однако, через имеющийся при турбулентном режиме ламинарный пограничный слой теплота передается только теплопроводностью.

Наличие ламинарного пограничного слоя при турбулентном режиме течения задерживает теплообмен и является основным термическим сопротивление процесса.

Коэффициент теплоотдачи “α”, характеризующий интенсивность теплопередачи при движении жидкости в трубах, определяется по различным уравнениям подобия; в зависимости от того, какой режим течения имеет место: ламинарный, переходный или турбулентный. Рассмотрим их.