Лекции по теплопередачи (Конвективный теплообмен, Word). 2. конвективный теплообмен основные понятия и определения

• Название: 2. конвективный теплообмен основные понятия и определения
• Дата: 04.11.2022
• Размер: 1.22 Mb.
• Имя файла: Лекции по теплопередачи (Конвективный теплообмен, Word).doc
• Тип: Документы; #770565
• страница: 2 из 7

2.2.3. Дифференциальное уравнение движения жидкости.
Дифференциальное уравнение движения является выражением закона сохранения импульса и устанавливает зависимость скорости движения жидкости от пространственных координат и времени.

Для вывода этого уравнения используем основной закон механики (второй закон Ньютона): равнодействующие всех сил, действующих на тело равна произведению массы на ускорение.

(86)

где - векторная сумма всех сил действующих на тело.

- полное произведение по скорости (по сути ускорения)

ρd- ничто иное как масса

Теперь, опираясь на основной закон механики выделим уравнение движения жидкости. Выделим в общем объёме жидкости элемент параллелепипед со сторонами dx;dy;dz=dV

На рассматриваемый параллелепипед в общем случае действуют 3 силы:

- сила тяжести

- сила давления

- сила вязкого трения с соседними параллелепипедами

Давление для начала пренебрегаем силами вязкого трения и получим уравнение движения невязкой жидкости в проекции на ось x(например газ – его вязкость мала)



(87)

Рассмотрим проекцию всех сил на ось x, в этом случае уравнение основного закона механики примет вид:

(86 а)

Ось x мы с вами направим вниз, поэтому проекция силы тяжести на неё будет: ρgdV (где g- ускорение свободного падения, ρdV - масса параллелепипеда)

Если в данной точке пространства имеем давление p, то сила, действующая на верхнюю грань нашего параллелепипеда будет pdydz, а сила действующая на противоположную грань будет .

Проекция на осьx равнодействующей силы давления будет:



Аналогично можно получить уравнение движения в проекциях на оси y и z. Однако заметьте, что в проекциях на них сила тяжести равна 0
(88)

(89)

Полученные нами уравнение (87), (88) и (89) является уравнение движения идеальной. т.е. невязкой жидкости и носят название уравнение Эйлера.

Для получения уравнения движения реальной, вязкой жидкости необходимо учесть силы внутреннего вязкого трения между слоями жидкости, движущейся с разными скоростями.

Согласно закона Ньютона, касательные напряжения “S”, возникают между перемещающимися с различной скоростью слоями жидкости пропорционально градиенту скорости:

(90)

где µ- динамическая вязкость (из справочника)

Рассмотрим плоский ламинарный поток жидкости, двигающийся в направлении оси x. При этом скорость ω_x меняется лишь в направлении оси y. В этом случае силы трения возникают только на боковых гранях.

Т.к. около левой грани скорость движения ω_x меньше, чем в самом элементе, сила трения будет равна “-Sdxdz” и направлена против движения и равна

Равнодействующая этих сил будет:

(91)

Подставим эти значения в уравнение (90):

(91)

(еще раз дифференцируем (90) поdy)

Уравнение (91) справедливо для одномерного случая. Если скорость изменяется в направлении всех осей, то равнодействующая сил вязкого трения, приложенных к рассматриваемому параллелепипеду dV определяется как: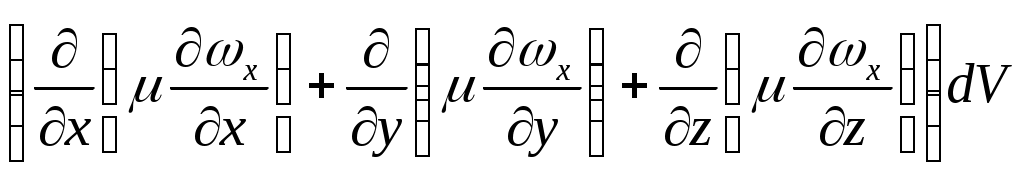



Если движущаяся среда имеет const вязкость, то окончательно выражение примет вид:



Уравнение движения вязкой жидкости (уравнение Навье - Стокса) можно получить, если к правым частям уравнений Эйлера (88), (89) и (87) прибавить силу вязкостного трения
(91)

(92)

(93)

Все члены этого уравнения имеют размерность :

ρg- сила трения

∂p/∂x- сила давления

- сила сопротивления

- сила инерции

В развернутом виде дифференциальное уравнение движения (Навье - Стокса) в проекции на ось х имеет вид:

(91а)

Для проекций на оси y и z вы это уравнение развернете сами.
2.2.4. Дифференциальное уравнение неразрывности.
Дифференциальное уравнение неразрывности выводиться на основе закона сохранения массы.

По аналогии с предыдущими уравнениями выделим в потоке движущегося жидкости элементарный объем dV со сторонами dx;dy;dz и вычислим массовый расход жидкости через него за время dτ.

В направлении оси “x” где время dτ поступает масса вещества m’_x равная m’_x=ρω_xdydzdτ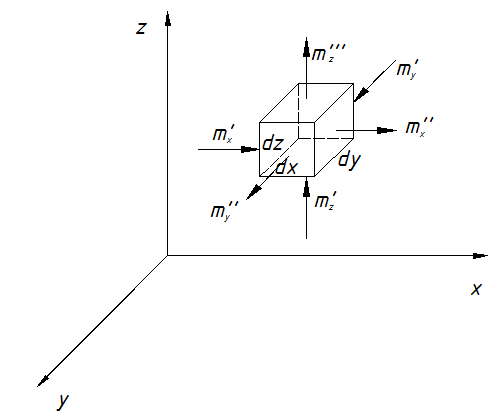



За это время, через противоположную грань параллелепипеда вытекает жидкость массойm”_x:



Изменение массы жидкости в элементарном параллелепипеде за время dτ в направлении оси х составит:



(94)

Аналогично запишем изменение массы жидкости за время dτ в направление осей y и z

(95)

(96)

Полное изменение массы в рассматриваемом параллелепипеде за время dτ получим проинтегрировав (96 – 96):



Это изменение массы вызвано изменением плотности жидкости (расширилась или сжалась) в параллелепипеде dV и равно изменению массы данного параллелепипеда во времени:



(97)

Получим дифференциальное уравнение сплошности. Для несжимаемой жидкости (вода, газ при малых скоростях движения ρ=const;p≠const)) ρ=const и уравнение принимает вид:

(98)

2.2.5. Условие однозначности для теплопередачи.
Итак, полученная нами система дифференциальных уравнений: теплообмена (79), энергии (84), движения жидкости (91-93) и сплошности (97) дает нам математическое описание механизма конвективного теплообмена при движении вязкой жидкости.

Эта система описывает целый класс явлений и имеет бесчисленное множество решений. Чтобы выделить из этого класса конкретное явление и соответственно получить конкретное решение, необходимо дополнить систему условиями однозначности: (они должны содержать все специфические особенности, относящиеся к данному процессу и влияющие на его ход).

Условие однозначности включает в себя:

1. 
   Геометрические условия – характеризуют форму, размеры и расположение поверхности описываемой средой (например: круглая вертикальная труба диметром d и длиной l )
   
2. 
   Временные условия – они нужны только для нестационарного процесса и формируют точно известные особенности протекания процесса по времени (питание в цилиндре ДВС)
   
3. 
   Граничные условия – характеризуют условия протекания процесса на границах тела (скорость иt жидкости в ядре потока, условие не протекания жидкости через границу (твердую стенку))
   
4. 
   Физические условия
   

Теперь, имея систему дифференциальных уравнений, дополненную условиями однозначности можно вести изучение процессов теплоотдачи аналитическим путем.

Однако сделаем весьма существенное замечание для аналитического пути исследования. Несмотря на то, что мы имеем возможность характеризовать теплоотдачу системой дифференциальных уравнений, которые вскрывают физическую сущность процесса и факторы от которых зависит α , система этих уравнений аналитически не решается.

Возможно лишь решение её численным методами, при условии принятия существенных допущений (уравнение Эйлера – метод Годунова, крупных частиц) с добавлением ряда эмпирических данных. Поэтому лишь некоторые из полученных решений могут быть использованы для решения технических задач.

Большую роль при исследовании процессов конвективного теплообмена и определения коэффициента теплоотдачи играют экспериментальные методы.

α обычно определяется в результате опытов, по результатам которых зависимость её от многих факторов процесса представляются в виде имперических формул, составленных на основе теории подобия.

Основная сложность экспериментального изучения теплоотдачи заключается в большом количестве различных случаев протекания этого процесса (большой и маленький двигатель). Для каждого случая приходиться проводить большое количество опытов и получать нужную зависимость (огромное количество формул, если вспомнить от скоростных факторов зависит α).

Поэтому, для возможности обобщения этих данных и выявления границ их применимости экспериментальные исследования должны быть построены на строгих теоретических основах. Такой теоретической базой современного эксперимента является, наряду с математической теорией планирования эксперимента – теория подобия.

Теория подобия позволяет на основе изучения какого – либо единичного процесса составить формулы для расчета всех процессов подобных ему. Кроме того она устанавливает при каких условиях процессы подобны. Она лежит в основе моделирования процессов, т. е. позволяет изучать процессы протекающие в сложных установках на основе их моделей.

Теперь, прежде чем мы рассмотрим с вами эмпирические формулы для расчетов теплоотдачи давайте познакомимся с этой значительной теорией – теорией подобия.

2.3 Основы теории подобия
Теория подобия это учение о подобии явлений.

Впервые с понятием подобия вы встречаетесь в геометрии, откуда эти термины и заимствованы.

Как известно геометрически подобные фигуры, например ∆ обладает тем свойством, что их соответственные углы равны, а сходственные стороны пропорциональны, т.е. 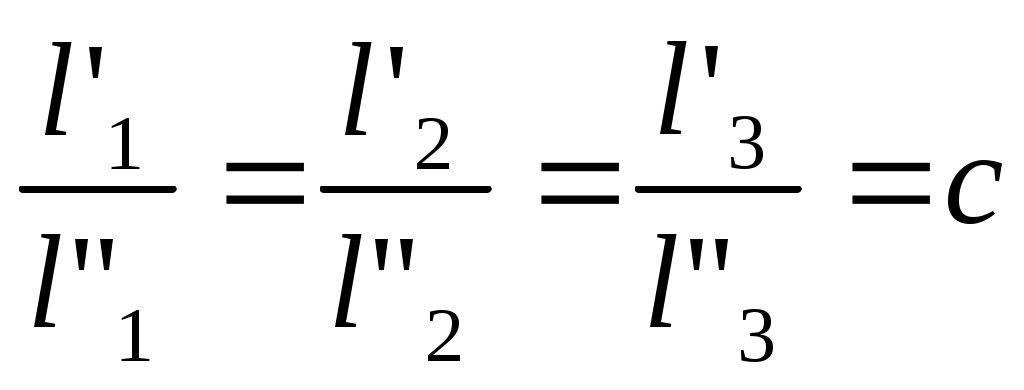, где с – коэффициент пропорциональности или контакта подобия.



Записанное нами условие является математическим выражения подобия. Оно справедливо для любых сходственных отрезков и фигур.

Зная условия подобия, можно решить ряд важных практических проблем (например из подобия ∆ определить высоту дерева не занимаясь измерением и т. д.)

Данное понятие подобия можно распространить на любые физические величины. Например можно говорить о подобии движения 2-х потоков жидкости (кинематического подобия), о подобии сил, вызывающих подобные между собой движения (динамического подобия),(игрушечный паровозик потащил вагон и настоящий), о подобии температур и тепловых потоков (тепловое подобия),(маленький и большой ДВС, большая и малая медная пластина)

Однако для того чтобы пользоваться этими понятиями необходимо установить условия подобия рассматриваемых физических процессов:

1. Понятия подобия в отношении физических явлений применимо только к явлениям одного и того же рода, которые качественно одинаковы и аналитически описываются одинаковыми уравнениями как по форме, так и по содержанию (остывание большой и малой медной пластины),(если аналитически описания 2-х явлений одинаково по форме – теплопроводность – диффузия, но различны по физическому содержанию, то можно говорить только об аналогии, но не как ни о подобии).

2. Обязательной предпосылкой физического подобия является геометрическое подобие. Это означает, что подобные явления всегда протекают только в геометрически подобных системах (остывание чайника и кастрюли или 2-х кастрюль - подобных).

3. При анализе подобных физических явлений сопоставлять между собой можно только однородные величины в сходственных точках пространства и сходственные моменты времени (т.е. величины имеющие один и тот же физический смысл и размерность), (температуру с температурой, скорость со скоростью).

4. Подобие двух физических процессов означает подобие всех физических величин, характеризующих рассматриваемый процесс. Например при теплоотдаче:

α=f(ω;t_c;t_ж;λ;ρ;C_p;α;β;µ;l­₁;l₂;…;F­)

подобия 2-х процессов теплоотдачи будет означать, что в сходственные моменты времени τ’=c_ττ”в сходственных точках пространства x'=c_xx”… любая величина характеризующая α в первом процессе пропорциональна одной с ней величине, характеризующей α во втором процессе: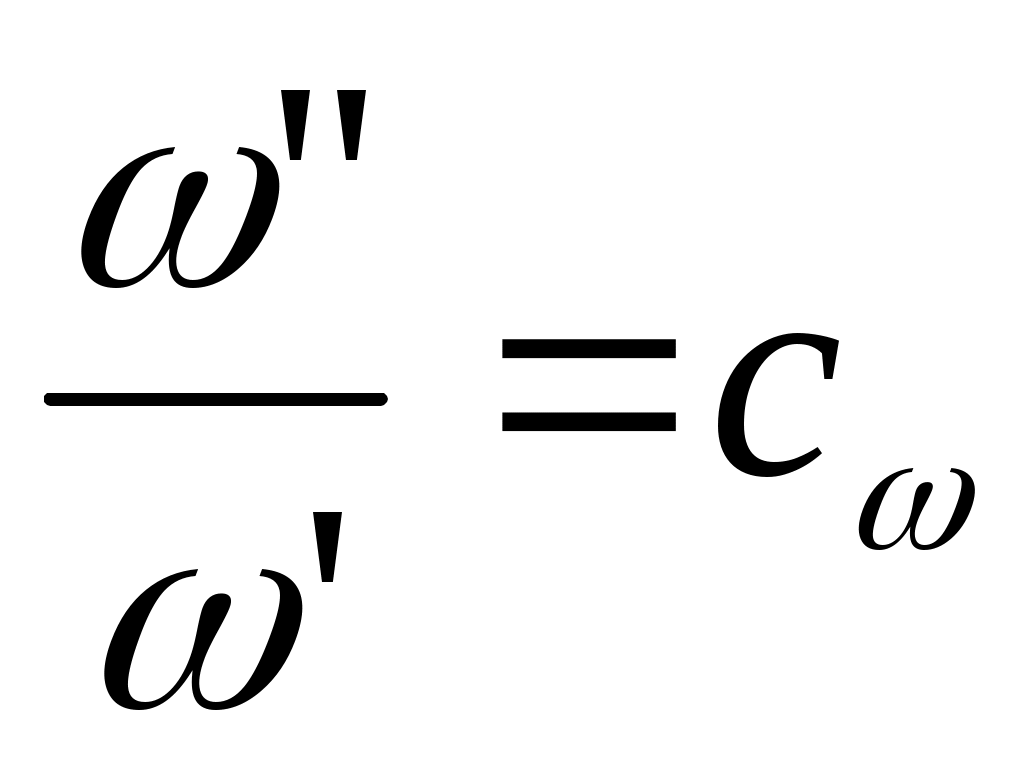

; ; …

где c_t;c_ω;c_l… - называется константами подобия. Они не зависят ни от координат ни от времени.

каждая величина может иметь свою константу подобия, т .е.

c_t≠c_ω≠c_l

Однако, для сложных процессов, которые определяются многими физическими величинами, константы подобия этих величин находятся между собой в определенных отношениях и их нельзя выбрать произвольно.

5. 
   Условия подобия 2-х физических процессов является наличие
   

соотношения между константами подобия физических величин, описывающих этот процесс. Константы подобия связаны между собой законом данного процесса.

Пусть мы имеем 2 подобных процесса движения жидкости, которые по 2-ому закону Ньютона характеризуют уравнение

Запишем это уравнение для соответствующих подобных процессов :

(а) – 1-ый процесс

(б) – 2- ой процесс

Так как мы рассматриваем подобные процессы однородные величины в них подобны и связаны в соответствии с условиями подобия через константы подобия. Выразим переменные второго процесса через переменные первого и const подобия:

p”=c_pp’;m”=c_mm’;ω”=c_ωω’;τ”=c_ττ’ (*)

полученные равенства подставим в уравнение (б)

…. (в)

Полученное уравнение (в) выражено через переменные первого процесса и будет тождественно уравнению (а), если в нем сокращаются множители составленные из констант подобия. Для того чтобы это было возможно долно выполняться равенство

или (г)

Это и есть то искомое условие подобия, которым ограничивается произвольный выбор констант подобия. В данном случае произвольно мы можем выбрать 3 любые константы подобия, а 4-ую будем обязаны определить по ним.

Это условие можно представить в более удобном виде, если уравнение (г) подставить вместо констант подобия их значения из соотношений (*)



т.е. для подобных процессов движения данный комплекс должен быть одинаковым.

Такие комплексы величин носят название критериев подобия или чисел подобия. Они всегда безразмерны



Критерием подобия называются безразмерными комплексами составленные из величин, характеризующих процесс. Нулевая размерность является основным свойством критерия подобия и служит проверкой правильности их составления. В подобных процессах критерии подобия равны. Полученный нами с вами критерий подобия. носит название критерий Ньютона и характеризует механическое подобие процессов движения. Чем выше Ne тем интенсивнее движение.

Критерии подобия можно получить для любого физического явления. Для этого необходимо только иметь аналитическую зависимость между переменными, характеризующими процесс.

Описание процесса в виде аналитической зависимости, хотя бы в виде неинтегрируемых дифференциальных уравнений является необходимой предпосылкой применения теории подобия. При этом критерии подобия, полученные из дифференциальных уравнений и уравнений полученных в результате их интегрирования являются одними и теми же. Это положение лежит в основе практического применения теории подобия.

Основные положения теории подобия обычно формируются в теории 3-х теорем.

Первая Теорема подобия устанавливает порядок получения критериев подобия, как безразмерных комплексов и связь между ними. В общей форме она формируется как:

Подобные между собой процессы имеют одинаковые критерии подобия (числа подобия)

Вторая Теорема подобия –об уравнениях подобия. Она устанавливает возможность предоставления результата интегрирования дифференциальных уравнений как функции от критериев подобия этого уравнения .

Она гласит, что любая зависимость между величинами характеризующими процесс может быть представлена в виде зависимости между критериями подобия этого процесса.

k₁;k₂…k_n f(k₁;k₂…k_n)=0

Это возможно потому, что числа подобия полученные из дифференциальных уравнений и их решений одни и те же. Т.е. решение дифференциальных уравнений можно представить как функцию чисел подобия, получаемых из самих дифференциальных уравнений.

Зависимость такого рода называется обобщенным или критериальным уравнением подобия. Эти уравнения обладают рядом важных свойств:

- Они тождественны дифференциальным уравнениям данного процесса и поэтому решение дифференциального уравнения можно заменить решением уравнения подобия. Решение последних, как правило находиться по опытным данным.

- Уравнения подобия одинаковы для всех подобных процессов, т.е. являются обобщенными.

- Уравнения подобия полученные по опытным данным являются чисто империческими, применять их можно только для подобных процессов в пределах изменения аргумента, которые наблюдались в опыте. На пределы изменения аргумента, в которых опыт не проводился, уравнение подобия не распространяются.

Третья Теорема подобия – даёт ответ на вопрос об условии подобия физических процессов, т.е. на вопрос: Какие процессы можно считать подобными?

Она формируется как: Подобны те процессы, условия однозначности которых подобны и критерии составленные из условий однозначности, численно одинаковы.

На основании этой теоремы оказывается необходимым выделить критерии, составленные из величин входящих в условие однозначности.

Критерием подобия в которые входят условия однозначности называются определяющими.

Таким образом теория подобия позволяет не интегрируя дифференциальных уравнений получить из них числа подобия и используя опытные данные составлять уравнения подобия, которые тождественны дифференциальным уравнениям и могут быть использованы для расчета всех процессов подобных изучаемому.

Теперь мы с вами, вооружены основами теории подобия и с её помощью давайте рассмотрим основные критерии подобия необходимые для решения дифференциальных уравнений теплоотдачи.