Лекции по теплопередачи (Конвективный теплообмен, Word). 2. конвективный теплообмен основные понятия и определения

• Название: 2. конвективный теплообмен основные понятия и определения
• Дата: 04.11.2022
• Размер: 1.22 Mb.
• Имя файла: Лекции по теплопередачи (Конвективный теплообмен, Word).doc
• Тип: Документы; #770565
• страница: 5 из 7

2.7.1.1. Теплоотдача при турбулентном режиме.
Итак, турбулентный режим характеризуется значение чисел Re>10⁴ и переносом теплоты внутри жидкости путем её перемешивания. При этом процесс протекает настолько интенсивно, что по сечению ядра потока температура жидкости практически постоянна. Однако через ламинарный пограничный слой теплота передается только теплопроводностью.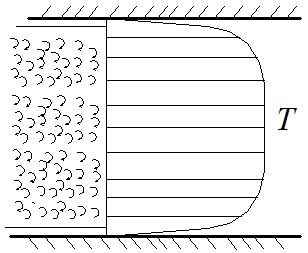



В результате обобщения многочисленных опытных исследований для случая турбулентного течения жидкостей в каналах было составлено следующие критериальное уравнение: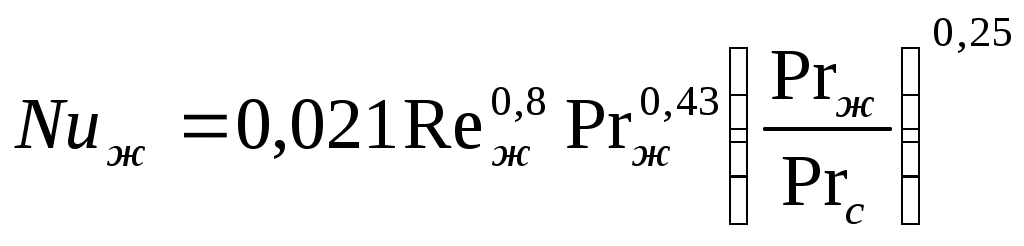

(1)

где Nu_ж- число Нуссельта, - характеризует теплоотдачу.

Re_ж- число Рейнольца, - характеризует режим течения.

- число Прандтля, характеризует собой соотношение между гидродинамическим и тепловым пограничными слоями. Является физическим свойством жидкости.

Индекс “ж” у чисел подобия показывает, что в качестве определяющей температуры, при вычислении чисел подобия принята средняя температура потока жидкости t_ж . Исключение составит число Прандтля Pr_с - взятое при средней температуре стенки.

Отношение 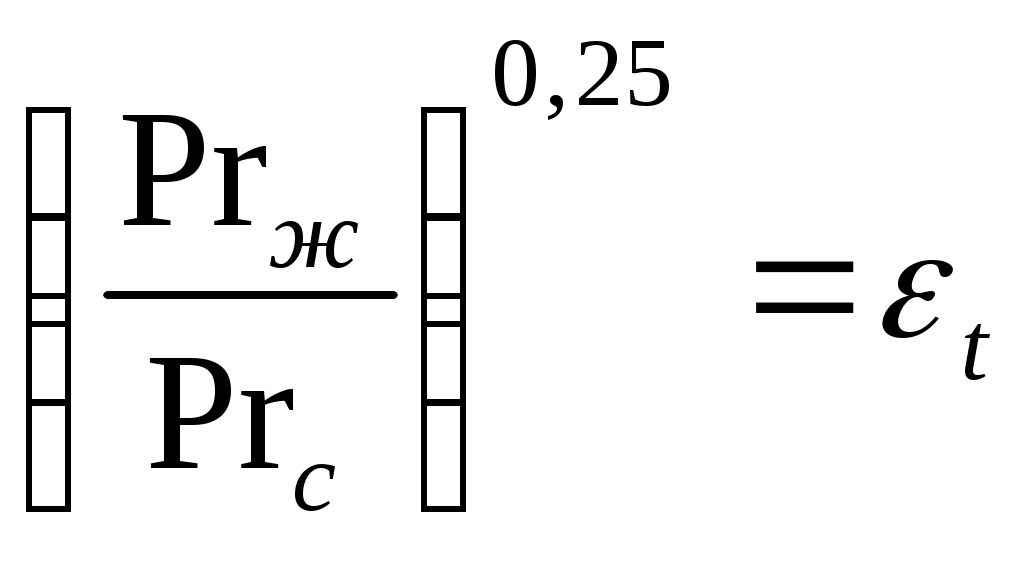- учитывает собой влияние на коэффициент теплоотдачи α направление теплового потока Q. Это связано с тем, что при нагревании текущей в трубе жидкости α несколько больше, чем при охлаждении.

Записанное нами уравнение (1) справедливо для всех жидкостей и газов, за исключением жидких металлов.

Оно может быть применено для каналов любого сечения: прямоугольник, треугольник, кольцо.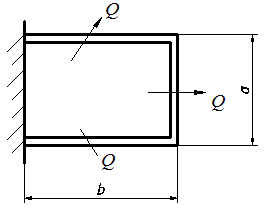
Однако для каналов не круглого сечения в качестве определяющего линейного размера в выражении чисел подобия берут эквивалентный диаметр





где f– площадь сечения канала.

П – плотный смоченный периметр.

Например: (см. рис.)

Для газов число Прандтля Pr мало зависит от температуры, поэтому для них ε_t=1. Для них полученное уравнение (1) существенно упрощается. Так как для воздуха и 2 – х атомных газов, для которых Pr=0,71 оно примет вид:

(2)

Отметим еще, что уравнения (1) и (2) справедливы только при течении в прямых каналах любого сечения при (l/d)>50. Для коротких труб (l/d)<50 коэффициент теплоотдачи α будет несколько больше, чем полученный по формулам (1) и (2). Это связано с влиянием участка тепловой стабилизации. Поэтому величину α, полученную из уравнения (1) для коротких труб умножим на поправочный множитель ε_l>1, учитывающий влияние начального участка тепловой стабилизации ε_l=f((l/d);Re)

Этот коэффициент выбирают по специальным таблицам и графикам, в зависимости от отношения l/dи числа Re (Михеев стр.91) (Селиверстов стр. 187)

ε_l ≈1,02…1,2для большинства рассматриваемых случаев.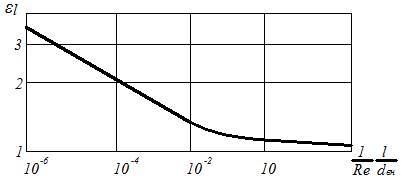



Для изогнутых труб, колен, отводов, змеевиков в α, определенное по уравнению (1),(2) так же вводиться дополнительный множитель. Необходимость его использования связана с тем, что при движении потока в изогнутой трубе за счет центробежных сил, возникающих при повороте потока, содержатся дополнительные завихрения и повторная циркуляция.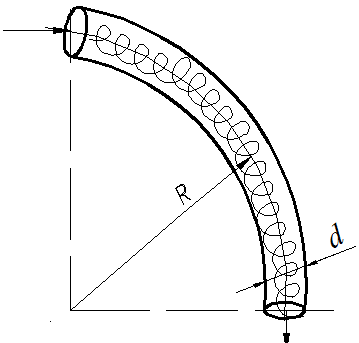


В результате этого толщина пограничного слоя уменьшается, а величина коэффициента теплоотдачи растет. Эта поправка достигает до 30%, поэтому применение змеевиков (как в самогонном аппарате) является очень эффективным средством улучшения теплоотдачи в теплообменниках.

Для змеевиковых труб:

d – диаметр трубы; R – радиус гиба.

Решив критериальное уравнение (1) определяют число Нуссельта, а по нему коэффициент теплоотдачи α.



В дальнейшем используя формулу Ньютона – Рихмана можно определить тепловой поток:







Устанавливая закономерности теплоотдачи при турбулентном движении жидкости в круглой трубе мы сказали, что формула: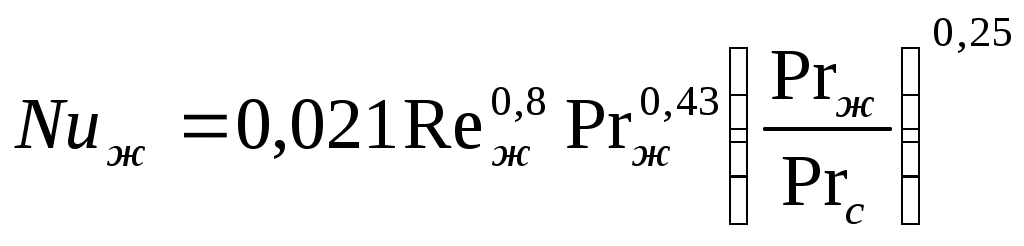



справедлива и для каналов сложного поперечного сечения. Примером такого сложного сечения может служить случай, когда в большой трубе расположено несколько более тонких (меньшего диаметра).

Поэтому имеющиеся у нас результаты и закономерности по течению в круглой трубе вполне естественно распространить и на продольно омываемые пучки труб.

Опытные данные установили (опыты А.Я. Иниятова), что в многотрубных пучках интенсивность теплоотдачи выше, чем при течении в трубе, и дополнительно зависит от взаимного расположения труб.

Повышение интенсивности теплоотдачи при продольном обтекании пучка труб связано с сильной турбулизацией потока при этом.

Критериальное уравнение подобия при этом имеет вид: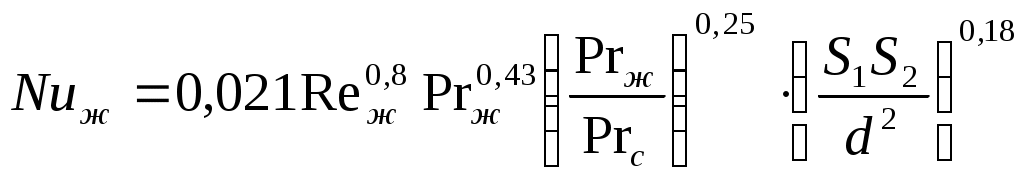

(3)

В качестве определяющего линейного размера, для вычисления значений чисел 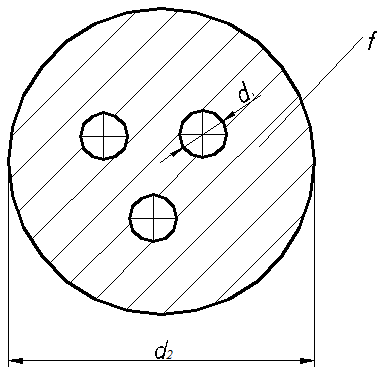и здесь применяется эквивалентный диаметр всего канала с пучком труб диаметром d и шагом S₁иS₂





f – площадь сечения.

П –периметр смоченный .
2.7.1. Теплоотдача при ламинарном режиме движения.
Ламинарный режим характеризуется значением числа Re<2000. Он характеризуется так же слоистым течением жидкости, в следствии чего теплота внутри неё передается в основном теплопроводностью и частично за счет перемешивания жидкости вызванного свободной конвекцией (следствие разности температур у стенки в ядре потока). Такое перемешивание вызывает некоторую турбулизацию потока, интенсифицирующую теплоотдачу. Максимальна она при вертикальном расположении трубы и противоположном направлении свободного и вынужденного движения.

Поэтому, можно сделать вывод, что при ламинарном режиме течения теплоотдача должна зависеть как от факторов вынужденного движения (Re), так и свободного (Gr)

Для расчета ламинарного режима существует большое количество видов уравнений. Однако ни одно из них не имеет видимых преимуществ. Я рекомендую вам следующее: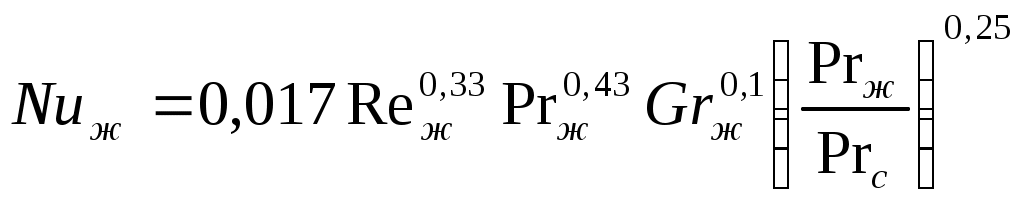

(3)

Все определяющие расчетные величины, входящие в уравнение (3) те же, что и в уравнении (1)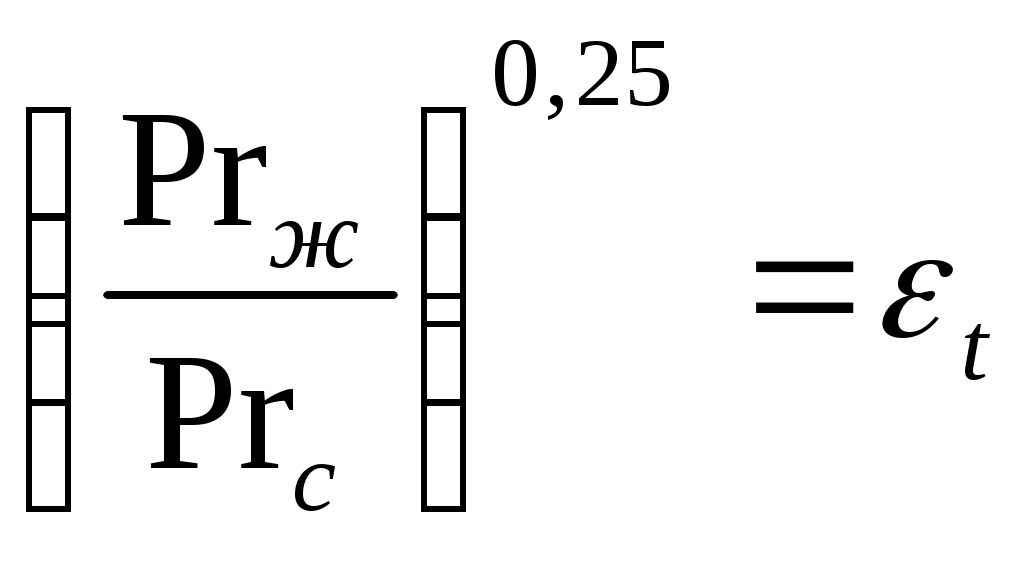
- число Нуссельта

- число Рейнольдса

- число Прандтля- физическое свойство жидкости.
- коэффициент учитывающий влияние на направления теплового потока (при нагревании жидкости больше чем при охлаждении).

Индексы “ж” и “с” показывают какие температуры (жидкости или стенки) являются определяющими при выборе физических параметров (λ,υ) входящих в числа подобия.

Мы видим, что при ламинарном режиме коэффициент теплоотдачи α в той же степени зависит от физических свойств жидкости как и при турбулентном 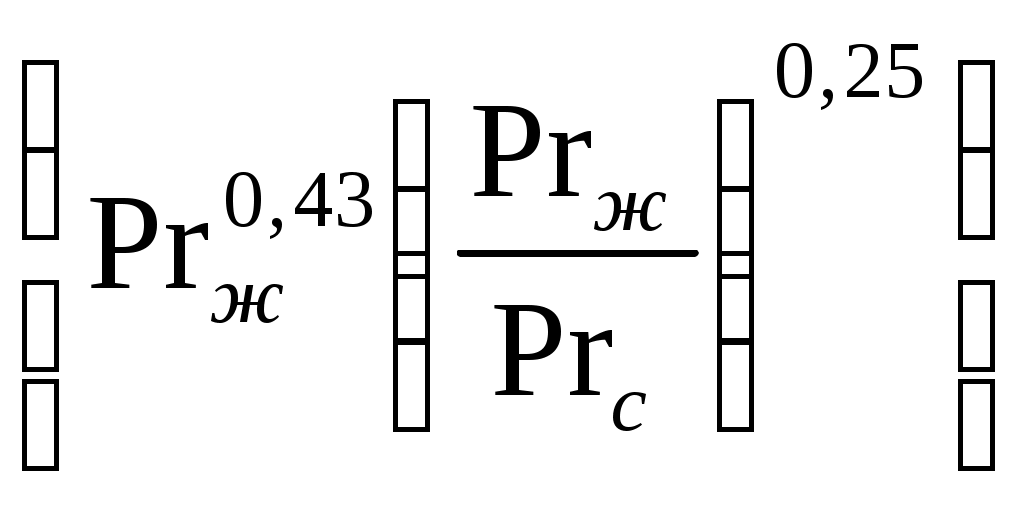есть в уравнении (1) и в уравнении (3). Однако, при ламинарном режиме α в меньшей степени, чем при турбулентном режиме зависит от скорости вынужденного движения потока (в уравнении (1) Re^0.8, а в уравнении (3) Re^0.33)

Дополнительно при ламинарном режиме 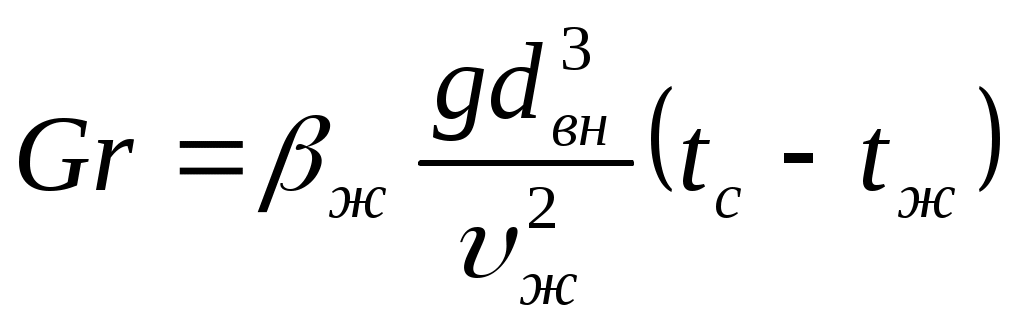зависит от свободного движения жидкости, возникающего поперек потока в следствии пазности температур в слоях жидкости. Свободное движение в уравнении подобия (3) учитывается числом Грасгофа:

- число Грасгофа, характеризует соотношение между подъемной силой, возникающей в следствии разности температур и силами вязкостного трения.

β- температурный коэффициент объемного расширения.

g- ускорение свободного падения.

Свободное движение способствует некоторому перемешиванию потока и улучшению теплоотдачи.

Приведенная нами формула (3) дает среднее по длине канала значение α при (l/d)>50. Она применима для любой жидкости и наиболее полно учитывает влияние направления теплового потока и естественной конвекции.

Для коротких труб, (l/d)<50по аналогии с турбулентным движением, выбирается поправочный множитель ε_l

Теперь поговорим о переходном режиме.

2.7.3. Теплоотдача при переходном режиме движения.
Этот режим характеризуется значениями числа Рейнольдса в пределах 2∙10³<Re<10⁴. В этом случае уравнение подобия записанные для ламинарного и турбулентного режимов течения неприменимы. Это связано с тем, что течение имеет неустойчивый характер, зависит от случайных величин. (может переходить из ламинарного в турбулентное и обратно) В соответствии с этим неустойчивой является и теплоотдача.

Поэтому, зависимость для переходного режима одной формулой не описывается и α оценивается приближенно по опытным данным.

Все три, рассмотренные нами случая теплоотдачи в каналах можно представить графически. Для этого критериальное уравнения подобия запишем в виде: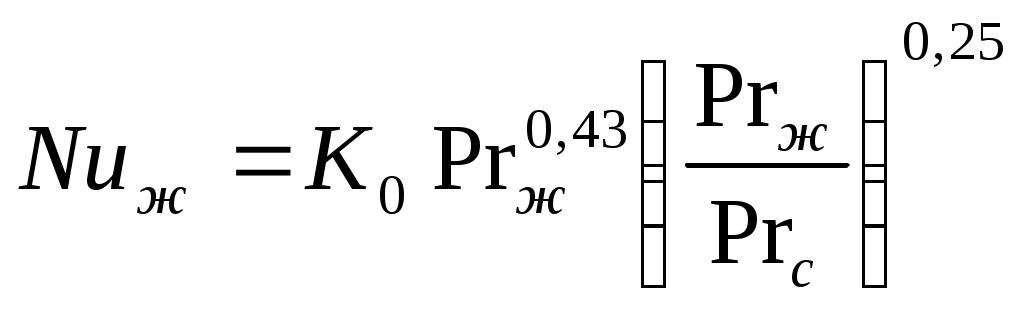

(4)

где K_o=f(ReиGr) и выбирается по таблицам в зависимости от значения Re. Gr – считается параметром.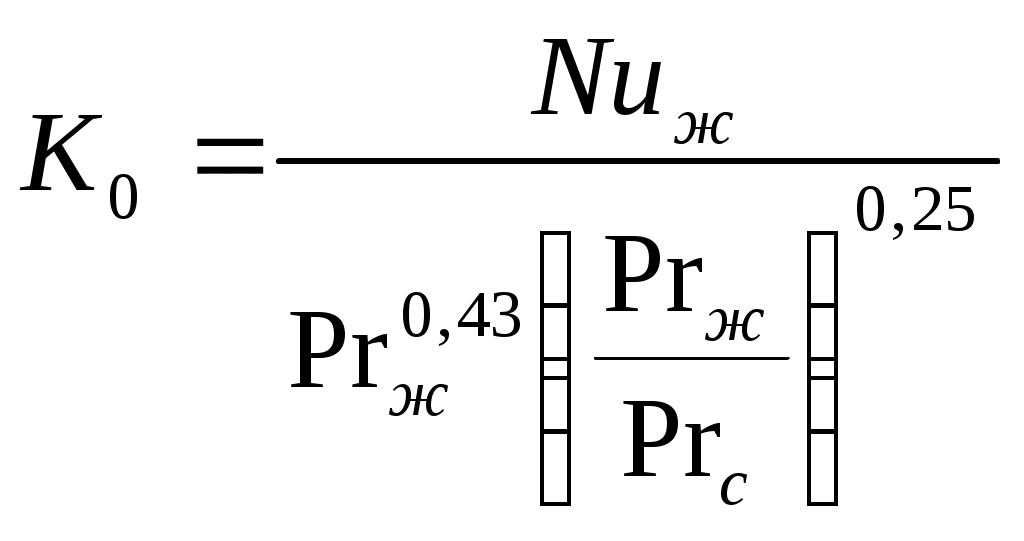



Нетрудно заметить, что величина стоящая в знаменателе “ 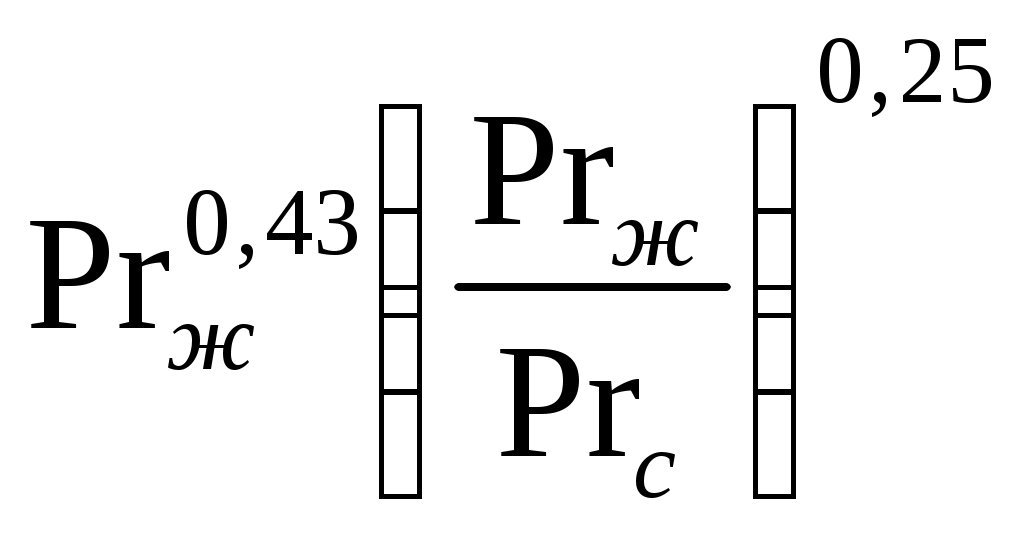” для заданного вещества (воздух, вода….) являются функцией физических свойств вещества (λ;α;υ) и для определенных жидкостей и определенных тепловых условий принимает постоянные значения.

График зависимости K₀ от Re можно построить в логарифмических координатах, принимая число Gr как параметр: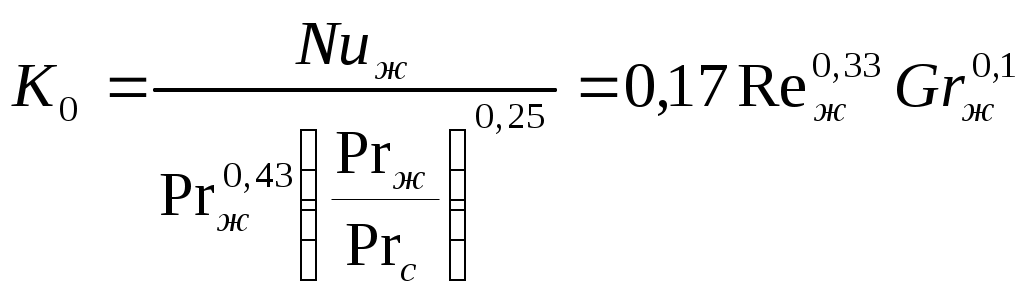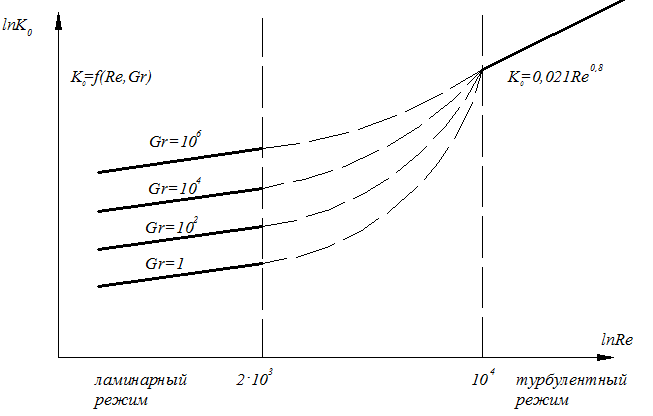


На ламинарном участке с ростом Gr интенсифицируется теплоотдача (так как растет K₀, а в него входит Nu). На турбулентном числом Gr можно пренебречь.
2.7.1.4. Теплоотдача в каналах с жидкими металлами.
Теплоотдача при течении жидких металлов (ртуть, натрий, висмут) в каналах существенно отличается от течения обычных жидкостей. Это обеспечивается тем, что жидкие металлы по своим физическим свойствам резко отличаются от обычных жидкостей. Для них характерно очень малая величина в следствии высокой теплопроводности.

Ртуть λ=10 – 12 Вт/мК

Висмут λ=12 – 17 Вт/мК

Натрий λ=60 – 80 Вт/мК

Благодаря этому, при течении жидких металлов в каналах, на теплоотдачу значительное влияние оказывает теплопроводность.

Уравнение подобия для случая подобия течения жидких металлов имеет вид:

(6)

Это уравнение получено опытном путем и справедливо при. 0,004<Pr<0,03;10⁴<Re<10⁶

При расчете течении жидких металлов в коротких трубах по аналогии с рассмотренным нами ранее случаем (l/d)<50 вводиться поправочный множитель ε_в, определяемые по таблицам в зависимости от Re и l/d

Теплоотдача жидких металлов значительно выше обычных жидкостей. Коэффициент теплоотдачи для них изменяется в пределах α=10⁴ – 3∙10⁴ . Поэтому жидкие металлы как теплоносители используются тогда, когда нужен интенсивный отвод тепла. Например, в ядерных реакторах.

Еще одним преимуществом жидких металлов, как теплоносителей является их высокая температура кипения при умеренных давлениях.


2.7.2 Теплоотдача при вынужденном движении жидкости вдоль плоской стенки.
При Движении жидкости вдоль плоской стенки появляется ряд особенностей по сравнению течения её в каналах.

Если стенка омывается потоком имеющим скорость ωто по сечению потока она остается неизменной. Резкое её изменение наблюдается только у самой поверхности стенки в пограничном слое. Здесь в следствии трения всегда образуется пограничный слой, внутри которого ϖ меняется от ω₀ - в ядре потока до “0” у стенки.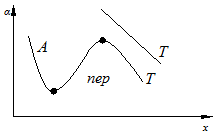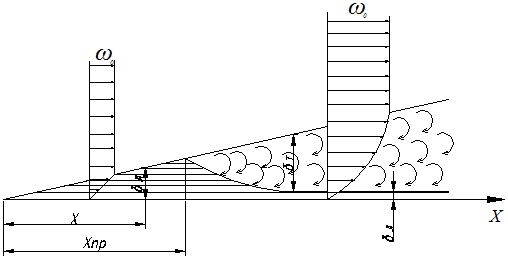



Опыт показывает, что у стенки образуется ламинарный пограничный слой, толщина которого по направлению течения жидкости возрастает.



υ- кинематическая вязкость

ω₀- скорость вне пограничного слоя (в ядре потока)

При достижении критического значения числа ламинарный пограничный слой переходит в турбулентный с тонким ламинарным подслоем. Толщина турбулентного пограничного слоя изменяется по закону:



Зная Re_кр мы всегда можем подсчитать длину участкаx_кр с ламинарным пограничным слоем и его максимальную толщину δ_кр.

;

Т.е. мы можем сделать вывод, что на определенных участках плиты характер движения жидкости в пограничном слое различен, а значит различно и теплоотдача. Это различие определяется родом жидкости, её скоростью и температурой.

На основании опытных данных для воздуха были получены следующие критериальные уравнения:

для турбулентного режима

для ламинарного режима

Недостатком приведенных формул является тот факт, что они не учитывают влияние начальной турбулентности потока, зависящей от внешних обстоятельств (сунул газету в поток воздуха). Кроме того при малых скоростях потока может сказаться и свободное движение жидкости (разность t_жи t_ст ). В этих случаях необходимо проводить проверочные расчеты по формулам для свободного движения жидкости и брать α как среднее для 2 – х расчетов.