Инвестиции_ Задание на РГР (1). 2. задание для расчетнографической работы по дисциплине инвестиции
 Скачать 193.28 Kb. Скачать 193.28 Kb.
|
2.2.4. Интегральные финансовые показатели проектаТак как инвестиционный проект осуществляется в течение длительного периода времени, то необходимо учитывать фактор времени. Это связано с тем, что с течением времени ценность денег уменьшается (рубль инвестированный (полученный) сегодня стоит дороже, чем тот же рубль через год). Для соизмерения расходов и доходов, получаемых в различные периоды времени, используют их приведение (дисконтирование) к моменту начала проекта (в нашем случае к 01.01.2017 г.). Дисконтирование осуществляется путем умножения притоков (оттоков), произведенных в t-й момент времени на коэффициент дисконтирования t3: 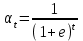 , (2.2) , (2.2)где е – ставка дисконта. Ставка дисконта задается инвестором и равна доходности, которую он хотел бы получить на инвестированный капитал. Нет единого подхода к определению этой величины. Ставка дисконта обычно равна банковской ставке в наиболее надежных банках. Также ставка дисконта может соответствовать уровню доходности, который преобладает на рынке в момент анализа выгодности инвестиционных проектов. Значение годовой ставки дисконта для каждого варианта расчетно-графической работы приведены в табл. 2.2. Формула (2.2) справедлива при неизменной ставке дисконта. Если же ставка дисконта меняется во времени и на k-м шаге расчета равна ek, то коэффициент дисконтирования равен 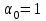 и и 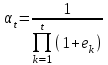 при t>0. (2.3) при t>0. (2.3)В данной работе предполагается, что годовая ставка дисконта неизменна. Однако в отчетных таблицах 2.9-2.11 используются периоды времени различной продолжительности: месяц, квартал, год. Зная годовую ставку дисконта можно рассчитать ставку дисконта на квартал ( 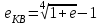 ), на месяц ( ), на месяц (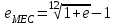 ). Таким образом, получаем, что при неизменной годовой ставке дисконта, ставка дисконта для некоторого периода времени изменяется в зависимости от длительности интервала времени. Например, коэффициент дисконтирования: ). Таким образом, получаем, что при неизменной годовой ставке дисконта, ставка дисконта для некоторого периода времени изменяется в зависимости от длительности интервала времени. Например, коэффициент дисконтирования:для 01.01.2017 г. 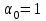 ; ;для 01.02.2017 г. 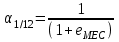 ; ;для 01.11.2017 г. 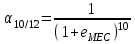 ; ;для 01.04.2018 г. (начало второго квартала 2018 г.) 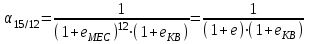 ; ;для 01.01.2019 г. 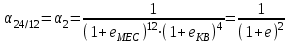 . .Обычно при анализе инвестиционных проектов данные о поступлениях (платежах) относят либо на начало, либо на конец соответствующего периода. Если поступления (платежи) были распределены равномерно в течение некоторого периода времени, то рекомендуется приписывать их к серединам соответствующих периодов [Четыркин]. В этом случае коэффициент дисконтирования имеет следующий вид 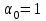 и и 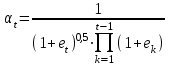 при t>0. (2.4) при t>0. (2.4)В данной работе будем считать, что поступления и платежи распределены равномерно в пределах периода времени, поэтому необходимо использовать коэффициент дисконтирования вида (2.4). Тогда коэффициент дисконтирования: для января 2017 г. (соответствует 15.01.2017 г.) 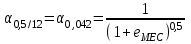 ; ;для февраля 2017 г. (соответствует 15.02.2017 г.) 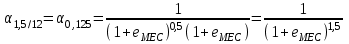 ; ;для ноября 2017 г. (соответствует 15.11.2017) 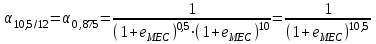 ; ;для второго квартала 2018 г. (соответствует 15.05.2018 г.) 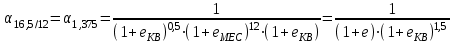 ; ;для 2019 г. (соответствует 01.07.2019 г.) 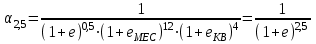 . .Коэффициенты дисконтирования t Таблица 2. 13
Для оценки инвестиционных проектов рассчитывают следующие показатели: 1. NPV (Net Present Value) – чистый дисконтированный доход (ЧДД)4. 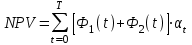 , (2.5) , (2.5)где Ф1(t) – сальдо денежных потоков от текущих операций (Строка 12 «Отчета о движении денежных средств»); Ф2(t) – сальдо денежных потоков от инвестиционной деятельности (Строка 25 «Отчета о движении денежных средств»). Если NPV<0, то проект не эффективен. Чем NPV больше, тем эффективнее проект. 2. PI (Profitability Index) – индекс доходности инвестиций (ИД)5 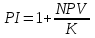 , (2.6) , (2.6)где К – дисконтированные инвестиции (абсолютная величина суммы дисконтированных элементов денежного потока от инвестиционной деятельности), 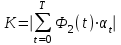 . (2.7) . (2.7)Если PI<1 – проект не эффективен. Чем PI больше, тем эффективнее проект. 3.IRR (InternalRateofReturn) – внутренняя норма доходности (ВНД)6 представляет собой ту ставку дисконта е, при которой величина NPV равна 0. Если рассматривать значение NPV как функцию от ставки дисконта е, то примерный график функции приведен на рис. 2.1. Иными словами, IRR является решением уравнения NPV(IRR)=0. (2.8) Рассчитанная величина внутренней нормы доходности сравнивается с требуемой инвестором величиной нормы доходности на капитал. Если IRR е, то проект считается эффективным. Р  ис. 2.1. График зависимости NPV от ставки дисконта е Чтобы найти IRR, необходимо решить нелинейное уравнение (2.8). Для этого выполняют несколько пробных расчетов значения NPV при различных значениях ставки дисконта e. Например, для ставки дисконтаравной 0.2, 0.4 или при других значениях. Так как такие вычисления являются достаточно трудоемкими, для приближенного вычисления IRR можно использовать метод линейной аппроксимации. Для этого выбирают два таких значения ставки дисконта е1 и е2, чтобы в интервале (е1, е2) функция NPV(e) меняла свой знак с «+» на «–». Далее применяют формулу 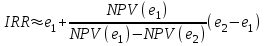 . (2.9) . (2.9)Для получения приемлемой точности оценки IRRделают несколько итераций, пока не достигнут приемлемой точности. В данной расчетно-графической работе итерационный процесс вычисления IRR можно прекратить либо если на очередной итерации длина интервала (е1, е2) меньше 1%, либо если для полученной оценки IRR выполняется неравенство NPV(IRR)<1. В случае использования для расчетов электронных таблиц Excel для нахождения значения IRR можно воспользоваться средством Подбор параметра. На вкладке Данные в группе Работа с данными нажмите кнопку Анализ «что-если» 4. PP (PaybackPeriod) – cрок окупаемости инвестиций. Это срок, за который можно возвратить инвестированные в проект средства. Различают «простой» срок окупаемости и срок окупаемости с учетом дисконтирования (Discounted Payback Period, DPP). Приведем пример расчета интегральных показателей инвестиционного проекта. Пример 1. Период инвестирования Т=4 года. Ставка дисконта е=0,15=15%. Будем предполагать, что элементы денежного потока в t-м году проекта распределены равномерно в пределах года. Для простоты при дисконтировании элементов денежного потока будем считать, что оттоки и притоки приходятся на середину года. Пример расчета Таблица 2.14
Чистый дисконтированный доход 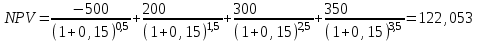 тыс. руб. тыс. руб.Дисконтированные инвестиции 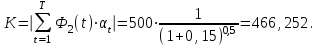 тыс. руб. тыс. руб.Индекс доходности инвестиций 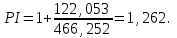 Для нахождения внутренней нормы доходности IRR первоначально выберем интервал [15%;40%]. NPV(15%)=122,053. 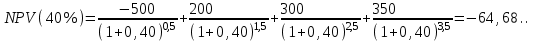 Тогда согласно (2.9) 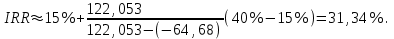 Так как 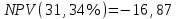 , поэтому новый интервал будет [15%; 31,34%]. Тогда на следующей итерации , поэтому новый интервал будет [15%; 31,34%]. Тогда на следующей итерации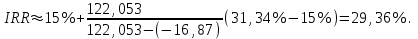 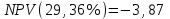 . Новый интервал [15%; 29,36%]. . Новый интервал [15%; 29,36%]. 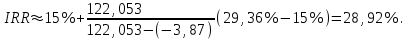 Так как 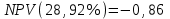 и данное значение NPV достаточно близко к нулевому значению, примем в качестве оценки величины IRR значение 28,92%. Отметим, что Excel дает оценку IRR равную 28,79%. и данное значение NPV достаточно близко к нулевому значению, примем в качестве оценки величины IRR значение 28,92%. Отметим, что Excel дает оценку IRR равную 28,79%.На рис. 2.2 приведен график для накопленного сальдо суммарного потока. 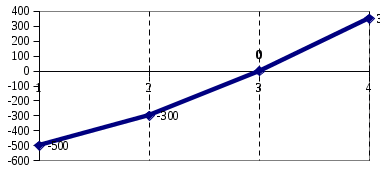 Рис. 2.2. График накопленного сальдо суммарного потока По данным о накопленном сальдо суммарного потока можно сделать вывод, что «простой» срок окупаемости соответствует середине третьего года, когда накопленное сальдо суммарного потока станет равно 0. Таким образом, срок окупаемости PP=2,5 лет. По данным о накопленном дисконтированном сальдо суммарного потока, представленным на рис. 2.3, можно сделать вывод, что срок окупаемости с учетом дисконтирования лежит в диапазоне от 2,5 до 3,5 лет, когда накопленном дисконтированном сальдо сменит знак с «–» на «+». 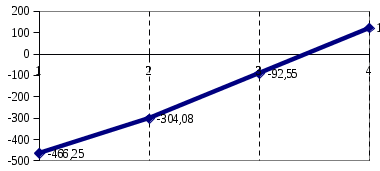 Рис. 2.3. График накопленного дисконтированного сальдо суммарного потока Методом линейной интерполяции можно уточнить срок окупаемости с учетом дисконтирования 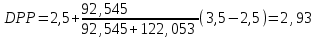 года. года.Рассчитанные показатели эффективности свидетельствуют, что данный проект эффективен. |

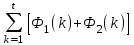 , тыс. руб.
, тыс. руб.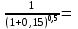 0,933
0,933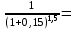 0,811
0,811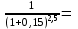 0,705
0,705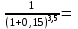 0,613
0,613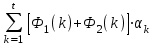 , тыс. руб.
, тыс. руб.