2 ркк. 21. Сапалы белгілер арасындаы байланысты зерттеу. Орайласты кестелерін Xuквадрат критерийіні кмегімен талдау
 Скачать 273.69 Kb. Скачать 273.69 Kb.
|
|
Салыстырмалықауіп-қатернемесемүмкіндіктерқатынасы Мүмкіндіктер қатынасы және салыстырмалы қауіп-қатер анықтағанда зерттеудің сипатын ескеру өте маңызды! Проспективтік зерттеу – бұл науқастар тобынын емдеу нәтижесін ұзақ уақыт бойы бақылау. Проспективтік зерттеулерде (зерттелетін топтар деректерді жинаудан бұрын қалыптасады) салыстырмалы қауіп-қатер есептеледі. Ретропективтік зерттеу – бұл алдын ала жүргізілген клиникалық зерттеулердің нәтижесін талдау. Ретроспективтік зерттеулерде (зерттелетін топтар деректерді жинаудан кейін қалыптасады), мүмкіндіктер қатынасы есептеледі. 23. Орайластық кестелерін түрлендіру. Фишердің нақты критерийі. Зерттелетін белгінің бақылау жиілігі мен сандық емес айнымалылардың деңгейлері жөніндегі деректер категорияланған деп аталады мұны орайластық кестесі деп аталады. Орайластық кестесін талдау, зерттеліп отырған көрсеткіштер салыстырылатын топтарда бірдей жиілікпен кездеседі (немесе кестенің бағандары мен қатарлары арасында өзара байланыс жоқ) деген нөлдік жорамалды тексеруге мүмкіндік береді Фишердің дәл критерийін қолдану ережесі: • Алғашқыкестеніалуықтималдығынесептеу. • Қатаржәнебағанбойыншаөзгермейтін қосындылар жағдайында кестені толтырудың қалған мүмкін нұсқаларын тұрғызу. • Алынғанбарлықкестелерүшінықтималдықтарды есептеу. • Алғашқыкестеніалуықтималдығынжәнеодан асып кетпейтін барлық ықтималдықтарды қосу. Зерттеудің негізгі міндеттері: Зерттелетін белгінің бақылау жиілігінің салыстырмалы шамаларын есептеу және олардың дәлдігі мен сенімділігін анықтау. Әртүрлі топтағы жиіліктердің салыстырмалы шамалары арасындағы айырмашылықтардың мәнділігі жөніндегі жорамалды тексеру (эмпирикалық және теориялық таралулардың сәйкестігі ). Теориялық деректерді есептеу Н0 – салыстырылатын деректер арасында маңызды айырмашылықтар жоқ. (а+с) белгісі кездесуінің жалпы саны бақыланған (n) көрсеткіштердің жалпы санының қандай пайызын құрайтынын есептеу. Табылған пайызды әрбір емдеу әдісінің белгісінің кездесу саны үшін сақтау. 24. Өміршеңдікті талдау әдістерінің ерекшеліктері. Өміршеңдік. Өміршеңдік функциясы. Цензурленген және цензурленбеген деректер. Өміршеңдікті талдау (Survival analysis) статистикалық әдістері биостатистикада ерекше орын алады. Медицинада өміршеңдікті талдау немесе оқиғаның (мысалы, өлім) пайда болғанына дейінгі уақытты талдау - пациенттің қандай-да бір бастапқы оқиғаның (мысалы, диагноздың қойылуы) басталған күнінен бастап өлшенген уақыт аралығынан артық өмір сүре алу ықтималдығын бағалауға мүмкіндік беретін статистикалық әдіс. Өміршеңдіктіталдауәдістерініңерекшелігі -олар толық емес деректерге қолданылады. Толық емес ақпараттардан тұратын бақылау цензурирленген бақылау деп аталады. Цензурирлеу термині алғаш рет 1949 ж. қолданылған. Талдау барысында цензурирленген деректерді қолдану, қарастырылып отырған әдістердің ерекшелігін анықтайды. Бұл әдістерде –өмір уақыты, өміршеңдік функциясы, өмір уақытының кестесі, өміршеңдік қисығы, Каплан-Мейер процедурасы сияқты ұғымдар қолданылады. Өмір уақыты – бұл қандай да бір оқиға пайда болғанға дейінгі уақыт. Оқиға: ауру симптомының дамуы, ауру ағзаның емге реакциясы,аурудың қайталануы (рецидив) немесе өлім. Өмір уақыты: аурудың дамуына дейінгі уақыт, емнің басталуы мен оған реакция болғанға дейінгі уақыт, ремиссия(денсаулықтың жақсара бастауы мен рецидивке дейінгі) уақыты, өлімге дейінгі уақыт. Цензурирленбеген деректер деп толык деректерді айтады: бақыланатын окиға барлык пациенттерде пайда болады және бастапқы нүкте мен соңғы нүкте (өлім) арасындагы уақыт аралығы белгілі. Цензурирленген деректер- бұл толық емес деректер: Пациенттердің барлығы әлі тірі, яғни зерттеу уақытында өлім уақиғасы болған жоқ және өмір уақыты белгісіз Зерттеліп отырған ауруға немесе ауруға қатысы жоқ себептерден өлім уақиғасы орын алады. Әрі қарай зерттеуге қатысушы болып саналмайды, зерттеуден белгісіз себептермен шығып кетуі мүмкін. Бұл жағдайлардың бәрінде зерттеліп отырған аурудың ұзақтығы белгісіз болып қалады. 25. Өмір сүру уақытының кестесі. Каплан-Мейер әдісінің көмегімен өміршеңдік функциясын бағалау. Өміршеңдік қисығы Өміршеңдік функциясы – бұл нысанның бақылаудың басталу мезетінен бастап t дан үлкен уақыт өмір сүру ықтималдығы: S(t) = P(T>t), немесе S(t) = 1 - P(T мұндағы P(T Өмір уақыты кестесін құрудың екі жолы: бірінші – Катлер –Эдерер тәсілі деректер құрамы үлкен болған жағдайда қолданылады. Бақылаудың барлық уақыты белгіленген уақыт аралықтарына бөлінеді және бөлек өмір уақыттары осы аралықтарға топталады екінші– Каплан – Мейер тәсілі тексерушілер саны аз болған жағдайда қолданылады. Әрбір жеке адам үшін дәл өмір уақыты қолданылады. Каплан Мейер әдісі - әрбір жеке адам үшін дәл өмір уақыты қолданылады. Бұл әдіс үлкен таңдамалар үшін де, кіші таңдамалар үшін де жарамды. Клиникалық зерттеулерде аурулардың әртүрлі топтарындағы өміршеңдікті салыстыру қажеттілігі туындайды. Нөлдік жорамал: екі топтағы өміршеңдік бірдей. Н0: S1(t)= S2(t) әдістер эквивалентті, Н1: S1(t)≠ S2(t) әдістер эквивалентті емес, немесе S1(t)> S2(t) 1-ші әдіс тиімдірек, немесе S1(t)< S2(t) 2-ші әдіс тиімдірек. Өміршеңдік қисықтарын салыстыру үшін арнайы әдістер қолданылады: Логрангілік тест, Йетс түзетуі, Гехан критерийі. 1. Өміршеңдікті Каплан - Мейердің мезеттік әдісі бойынша анықтаймыз. 2. t уақыт мезетінен артық өмір сүре алу ықтималдығы анықтау. 3. Өміршендік (Тірі қалғандар-дың кумулятивтік үлесі) S(t)анықтау. 4. Есептеуге ыңғайлы болу үшін деректерді өміршеңдікті есептеу кестесіне енгіземіз. 5. Өміршендік қисығын тұрғызу. 6. Қорытынды. 26. Екі өміршеңдік қисықтарын салыстыру. Ең алдымен сұраққа жауап бермес бұырын өміршеңдік функциясы туралы айта кететін болсам – яғни ол, нысанды бақылаудың басталу кезегінен бастап t-дан үлкен уақыт өмір сүру ықтималдығы, яғни: S(t) = P(T>t), немесе S(t) = 1 - P(T Бұндағы, P(T>t)- t уақытқа дейінгі болған оқиғаның (апаттың) пайда болу ықтималдығын айтмыз. Және S(t) функцияясының қасиетін айта кеттін болсам: S(t)=1 егер бұндағы t=0; S(t)=0 егер бұндағы t=∞. Клиникалық зерттеулерде әр түрлі топтардағы аурулардың өміршеңдігін салыстыру қажеттілігі жиі туады. Бұндағы нөлдік жорамал: екі топтағы өміршеңдікке де бірдей болады. Н0 : S1 (t)= S2 (t) әдістерэквивалентті, Н1 : S1 (t)≠ S2 (t) әдістерэквиваленттіемес, немесе S1 (t)> S2 (t) 1-ші әдістиімдірек, немесе S1 (t)< S2 (t) 2-ші әдістиімдірек. ӨміршеңдікқисықтарынсалыстыруүшінарнайыЛогрангілік тест, Йетс түзетуі, Геханкритерийі сияқты әдістер қолданылады. Екі топты салыстыру жағдайын қарастыратын болсақ. 1. Логрангілік критерий немесе логарифмдік рангілік критерий – екі өміршеңдік қисығын салыстыру үшін қолданылатын параметрлік емес критерий. Бұл критерийді алғаш рет Натан Мантѐл ұсынған және оны Ричард және Джулиан Пето «логранк критерийі» деп атаған. Йейтс түзетілуі Логрангілік критерий үшін Йейтс түзетілуі: 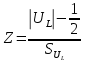 формуласымен есептеледі. Біз өміршеңдікті салыстырудың қарапайым әдісін, атап айтқанда екі топтағы өміршеңдікті салыстыруды қарастырдық. Екіден көп топтардың өміршеңдіктерін салыстыру принциптерге негізделген. Оған мысал келтіретін болсам, қарт адамдарға амбулаторлық емдеу стационарлық емдеуге қарағанда тиімді және арзан. Алайда амбулаторлық бақылау госпитальдауды қажет ететін адамдарды жеткілікті айқындауға мүмкіндік бере ме? Яғни бұндағы қарт адамның жалпы жағдайын бағалау үшін күнделікті үй жұмысының шкаласы деп аталатын ұғым енгізіледі. Осы шкаланың болжамдық бағасын білу үшін жас мөлшерлері шамамен бірдей адамдарға зерттеу жұмыстарын жүргізеді. Орта жасы 78,4 жыл, стандартты ауытқу 7,2 жыл. 4 жылдық бақылаудан кейін төмендегідей нәтижелер алынды және есептеуге ыңғайлы болу үшін деректерді өміршеңдікті есептеу кестесіне енгізіп есептейміз. Бұнда ең алдымен өміршеңдікті Каплан - Мейердің мезеттік әдісі бойынша анықтаймыз. Одан кейін t уақыт мезетінен артық өмір сүре алу ықтималдығы анықтап аламыз. Және өміршендік (Тірі қалғандардың кумулятивтік үлесі) S(t) анықтаймыз. Есептеуге ыңғайлы болу үшін деректерді өміршеңдікті есептеу кестесіне енгіземіз. Өміршендік қисығын тұрғызамыз. Соңында қорытындылаймыз. Өміршендік қисығын тұрғызу туралы нақты айта кететін болсам, бұнда диаграммадағы нүктелер кем дегенде біреуі қайтыс болған сәттерге сәйкес келуі қажет. Және бұндағы нүктелер қадам сызығымен қосылады, бұл график өмір сүру қисығын бағалайды. Сонымен қатар, салынған қисықты сипаттауға және жалпылауға болады. Қорытындылайтын болсам, медицина саласында, мысалы зерттеулерде аурулардың әртүрлі топтарындағы өміршеңдікті салыстыру қажеттілігі туындап жатады, сол кезде осы жоғарыда көрсетілген әдіс арқылы есептеу жүргізіледі. Және де Логрангілік критерийді алғаш рет Натан Мантел ұсынған және оны Ричард және Джулиан Пето «логранк критерийі» деп атаған. Осы жағдайды мысал ретінді түсіндірсек, мысалыға ауруханада жаңа дәріні сынау жүргізілу қажет делік. Ол үшін екі бақылау тобын салыстырады: бірінші топтағы адамдар жаңа дәріні, ал екінші топтағылар ескі дәріні қабылдайды. Сосын жаңа дәрінің қаншалықты тиімді екенін анықтау қажет.Әрине осындай салыстыру жағдайлары медицина саласында жетерлік, сол жағдайда Екі өміршеңдік қисықтарын салыстыру арқылы жағдайды шеше аламыз. 27. Дисперсиялық талдау. Бірфакторлық дисперсиялық талдауды жүргізу әдісі. Ең алдымен дисперсиялық талдау ұғымына тоқтала кететін болсам – ол кездейсоқ таңжалған әртүрлі топтардың орта мәндерін салыстыру үшін, яғни бірнеше тәуелсіз топтардың бір бас жиынтыққа жататындығын немесе жатпайтындығын анықтау үшін қолданылатын талдау әдісі болып табылады. Яғни, орта мәндердің арасындағы айырмашылықтарды анықтау үшін дисперсияларды қолданамыз. Дисперсиялық талдау деп таңдама дисперсияларды салыстыру арқылы екі немесе бірнеше таңдамаларды зерттеуге арналған статистикалық әдістер тобын айтамыз. Және міндеттерін айта кеттін болсам, белгіленген немесе кездейсоқ болуы мүмкін бірнеше деңгейлермен сипатталатын факторлардың ықпалын зерттеу болып табылады. Мысал келтіретін болсам ,А факторы – үш деңгейден тұратын аурудың ауырлығы: жеңіл, орта, ауыр болып өтуі мүмкін. Дисперсиялық талдау 3 факторлы талдауға бөлінеді, яғни олар: Бірфакторлы; Екіфакторлы; Көпфакторлы; Және бұлардың ішіндегі бірфакторлы дисперсиялық талдау туралы айта кететін болсам-ол бір фактордың ықпалы тексерілетін дисперсиялық талдау. Яғни ол, зерттелетін фактордың тәуелді айнымалыға әсері туралы гипотезаны тексеруге мүмкіндік береді. Және оның негізгі идеясы: Таңдама дисперсияны екі компенентке бөлу болып табылады: оның біріншісі факторлық дисперсия болса, екіншісі қалдық дисперсия болып табылады. Бір факторлы ANOVA (бұндағы ANOVA туралы түсінік бере кететін болсам – ол дисперсияны салыстыру арқылы орташалар арасындағы айырмашылықтың маңыздылығын зерттейді) математикалық моделі тәуелді айнымалының жалпы өзгергіштігінде оның екі құраушысын бөлуді қамтиды: өзгергіштіктің топаралық құраушысы фактордың әсерінен орташа мәндердің айырмашылығына байланысты; өзгергіштіктің топ ішіндегі құраушысы ескерілмеген себептердің әсерінен болады. Өзгергіштіктің осы екі құраушысының арақатынасы фактордың әсерінің статистикалық маңыздылығын анықтайтын негізгі көрсеткіш болып табылады. Дисперсиялық талдауды жүргізу әдісі туралы айта кететін болсам: 1. Нөлдік және балама жорамалдарды құрамыз. Бұндағы Н0 : топтық бас орта мәндер тең болады, және таңдама орталар арасындағы айырмашылықтар кездейсоқ, факторлар оларға ықпал етпейді. Ал, H1 : таңдама орталар арасындағы айырмашылықтар кездейсоқ емес және оларға фактор ықпал етеді. 2. α мәнділік деңгейі беріледі ( мысалы, α=0,05 немесе α=0,01). Және осы бірфакторлы дисперсиялық талдауға мысал келтіретін болсам: Яғни, темекі шегудің тыныс алу жолдары ауруларына ықплы. Белгілі бір жас шамасы категориясындағы үлкейген тұрғындар арасында екі жыл ішінде тыныс алу жолдары ауруына ұшыраған адамдардың саны белгілейміз. Зерттеу мақсаты темекі шегудің тыныс алу мүшелері ауруларына ықпалын статистикалық дәлелдеу болып табылады. Әрқайсысы 4 адамнан тұратын 3 топ кездейсоқ таңдалынып алынды, олардың: І топ-темекі шекпейтіндер; ІІ тобы темекі шегу стажы 5 жылға дейін, ІІІ тобы темекі шегу стажы 5 жылдан көп. Бұндағы фактор деңгейлері: А1, А2, А3 – темекі шегу стажы. Темекі шегу факторына жауап – тыныс алу жолдары ауруларының саны. Дисперсиялық талдау жүргіземізу арқасында: 1. Жорамалдарды ұйғарамыз; Және бұндағы H0 - темекі шегу тыныс алу мүшелері ауруларына ықпал етпейді. Ал, H1 - темекі шегу тыныс алу мүшелері ауруларына маңызды ықпал етеді. Қорыта келгенде дисперсиялық талдау- бұл екіден артық топтардың орта мәндерін салыстыру үшін, яғни бірнеше тәуелсіз топтардың бір бас жиынтыққа жататындығын немесе жатпайтындығын анықтау үшін қолданылатын талдау әдісі. Дисперсиялық талдауды алғаш рет ағылшын ғалымы, математик және генетик Рональд Фишер 1938 ж. Дисперсиялық талдауға мынадай анықтама берген: Дисперсиялық талдау-«бір себептерден болатын дисперсияны екінші бір себептерден болатын дисперсиядан айыру». 28. Дисперсиялық талдау көмегімен тексерілетін статистикалық жорамалдар. Фишердің F-критерийі. Фишердің F-критерийі. 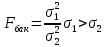 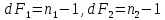 К тәуелсізтаңдамалар бар болсынжәнеолардыңәрқайсысыжекетоптыанықтайды. Таңдамалар көлемдері - nі, орта мәндерхі және орта квадраттықауытқуларSi (i= 1,2,…,k) болсын. Таңдамалардыңжалпы көлемі: n = n1+n2+…+nk 1-шіден нөлдікжәнебаламажорамалдардыанықтаймыз: Н0: Бас жиынтықтыңбарлықтоптық орта мәндерітең: х1=х2=...=хк Н1: Бас жиынтықтың барлық топтық орта мәндері тең емес. 2-шіден қажетті деректерді K таңдамалардан алу. MSфакт мен MSқалд есептеу, егер MSфакт < MSқалд болса, онда Н0 қабылданады, егер MSфакт < MSқалд болса, онда F критерийін есептейміз. 3-шіден критерий статистикасын есептеу: Fбақ 4-шіден α мәнділік деңгейіне сәйкес (α = 0,05 немесе α= 0,01) Фишер таралуының сыни мәнін арнайы кестеден табу. 5-шіден F критерийініңстатистикасынсынинҥктеменсалыстыру. 6. Н0 жорамалғақатыстышешімқабылдау: ЕгерFбақ Егер Fбақ > Fсыни болса, онда нөлдік жорамал жоққа шығарылады және фактордың ықпалы маңызды болып табылады. Дисперсиялық талдауды қолдануға қойылатын шарттар: 1. Әрбір таңдама басқа таңдамалардан тәуелсіз. 2. Әрбір таңдама зерттелетін бас жиынтықтан кездейсоқ түрде алынған. 3. Бас жиынтық қалыпты таралған. 4. Топтардың бас дисперсиялары бірдей. Ескерту: Бұл талаптардыорындау аса маңызды. Сондықтандисперсиялықталдауды жүргізбес бұрыналдыменбарлықсалыстырылатынтоптардыңтаралуынқалыптылыққатексеружәне осы топтардағыдисперсиялардыңтеңдігінтексеруқажет. Бұлшарттардыңеңболмағандабіреуібұзылғанжағдайдадисперсиялықталдаудықолдануғаболмайды. Мұндайжағдайдабірфакторлы ANOVA-ныңпараметрлікемесаналогыКрускал – Уоллис критерийінқолдануқажет. 29. Дисперсиялық талдау. Екі факторлық дисперсиялық талдау жүргізу әдісі. Екіфакторлы дисперсиялық талдау – біз екі фактордың әсерін талдап қана қоймай оның байланысын бағалай аламыз. Қазіргі таңда тірі организмге бір ғана фактор әсер етіп қоймайды.Мыс:өсімдіктің жоғары сапалы өнімін алу үшін оның генетикалық құрылымы,топырақ типі,жарықтануы,температура және т.б. факторлар әсерін анықтауымыз қажет.Сондықтан да осындай типтегі тәжірибе жүргізу үшін екіфакторлы дисперсиялық талдау қолданылады. Қалыпты үйлестірілген кездейсоқ Х шамасы мәндерінің қалыптасуына А және В факторларының бірмезгілдегі әсерін бағалайық. А факторы әсері m деңнейдентұрады (А1,, А2,… Аm ), ал В факторы n-( В1, В2,…Вn) . Қарапайымжағдайдағыэксперименттердіңнәтижесінқарастырсақ, бұлкездефакторлықдеңгейлердіңәрбіржұптарының (Аi, Bj) ( i=1.2…,m; j=1.2…,n) әсерікезінде Х шамасынабірғанабақылаужүргізілетінінбайқауғаболады. Қалыптыүйлестірілгенкездейсоқ Х шамасымәндерініңқалыптасуына А және В факторларыныңбірмезгілдегіәсерінбағалайық. А факторы әсері m деңнейдентұрады( А1,, А2,… Аm ), ал В факторы n-( В1, В2,…Вn) . Қарапайымжағдайдағыэксперименттердіңнәтижесінқарастырсақ, бұлкездефакторлықдеңгейлердіңәрбіржұптарының (Аi, Bj) ( i=1.2…,m; j=1.2…,n) әсерікезінде Х шамасынабірғанабақылаужүргізілетінінбайқауғаболады. Екіфакторлы дисперсияанализде - жорамалтуралыбақылаупараметрініңматематикалықболжанымыныңекіфактордыңтүрлідеңгейлеріндетексеріледі. Айталық, бірдейбұйымныңшығарылымытүрлікәсіпорындарменөндіріледі, қолданыстағытүрліжеткізушілерді. Мунда екі фактор: кәсіпорынжәнежеткізушілер. Тексеругеқажеткежорамалтуралышығаберістіңбақылаупараметрінің(айталықбұйымныңсапаларының) математикалықболжанымыныңтүрлідеңгейлерінде(кәсіпорындарда) жәнеекіфактордыңтүрлідеңгейлерінде(жеткізушілерде). Осы қалыптаx1 жәнеx2 кіретінайнымалылардискреттімағыналардықабылдайды. Екіфакторлыдисперсиялық анализ: келесіалғышарттарданегізделеді: Екіфакторлыдисперсиялыанализдыңесептеушікестесінқараймыз. Мейліx1 kтүрлімағынанемесеx1 факторынkдеңгейлердіңқабылдайды, x2 mтүрлімағынанемесеx2 факторынmдеңгейлердіңқабылдайды: x1 жәнеx2 факторыныңдеңгейлеріматематикалықболжанымынаәсеретпесе ,солбарлыққадағалауларөзіменіріктеменібір бас құрамнанұсынады. Сонда бас құрамныңдисперсиясынбағалауғаболадыкелесітәуелсізсарапшылықтарарқылыyортаныңмағыналарының бас-басы үшінx1 немесеx2 факторыныңдеңгейлеріненнемесе орта арифметикалықyдисперсиясініңсарапшылықтарының бас-басы үшінx1 немесеx2 деңгейлерісияқты. БірфакторлыбытыраңқыанализдабіріншісарапшылықS2ур деңгейініңекідисперсиясыныңсарапшылығымен - S2ош қатесініңдисперсиясініңсарапшылығыменаталатын. Біріншіжәнеекінші фактор үшін: S2yp1=n*m*Σ(yj-y…)2/(k-1) S2yp2=n*k* Σ(yi-y…)/(m-1) x1 факторыныңдеңгейініңықпалыжәнебас x2 математикалықболжанымболмайды, сол F1 = S2ур1/S2ош, F2 = S2ур2/S2ошқатынастарыжәне Fвз = S2вз/S2ошФишердіңтаратушылқыныңзаңынабағынышты. Осытаратушылықтыңмінездемелері S2ур1 денсарапшылығыныңеркіндігініңдәрежесініңсанының, S2ур2, S2взжәне S2ош(алымныңνеркіндігініңдәрежесініңсандары 1= (k - 1), ν2= (m - 1), νвз= (m - 1) * (k - 1) жәнеош=m*k* (n - 1) бөлімініңν ) тәуелдіболадыжәне x1 факторыныңбарлықдеңгейлеріүшінқайшыкеліптур, x2 және x1*x2 оныңәрекеттестіктері F Осыны түсіну үшін мысал келтірсек: ғалымдардың зерттеуі бойынша, үлкен ерлер мен әйелдердің арасындағы доминанттылықты алатын болсақ, немесе жанұяның тұңғыш балаларымен кенжелерін салыстырсақ, біздің ойлауымыз бойынша бірінші жағдайда ер адамдар доминанттылық көрсетеді, ал екінші жағдайда тұңғыш балалары доминанттылық көрсетеді. Бірақ, туу көрсеткіші бойынша ер адамдар көп туылса олар да доминанттылық төмендейді, ал әйел адамдарда керісінше көбейеді. Ал, кенже балаларда доминанттылық басым, себебі барлық жанұя мүшелерінің бақылауы сол балада болады және барлығы сол балаға көмектеседі қандай жағдай болмасын. Қорытындылай келе, екіфакторлы дисперсиялық талдау бір уақытта екі фактор әсерін анықтайтын ең тиімді әдіс болып табылады.Ол бірфакторлы дисперсиялық талдаудың әдісіне ұқсас.Ерекшелігі фактораралық байланысты да анықтайды.Осы талдау әдісі арқылы екіден астам топтарға әсер ететін екі факторды дұрыс бағалауға мүмкіндік береді. 30. Бірфакторлық талдаудан көпфакторлық талдаудың негізгі ерекшеліктері. Өзара әрекеттесу эффектісі. Факторлардың кездейсоқ шама өзгергіштігіне әсерін зерттейтін статистика бөлімін дисперсиялық талдау деп атайды. Бұл екіден артық топтардың орта мәндерін салыстыру үшін, яғни бірнеше тәуелсіз топтардың бір бас жиынтыққа жататындығын немесе жатпайтындығын анықтау үшін қолданылатын әдіс. Бұл бірнеше топтарды зертеуде қолданатын айырмашылық немесе ұқсастық ережелері. Таңдауды гомогендікте және себеп-зерттеу байланыстарында бақылау кезінде,Р.Фишермен жасалынған жиі кездесетін әдіс түрі. |
