2 ркк. 21. Сапалы белгілер арасындаы байланысты зерттеу. Орайласты кестелерін Xuквадрат критерийіні кмегімен талдау
 Скачать 273.69 Kb. Скачать 273.69 Kb.
|
|
Дисперсиялық талдау-бір себептерден болатын дисперсияны екінші бір себептерден болатын дисперсиядан айыру. Бір факторлы дисперсиялық талдау Бұл осы факторларға көптеген кездейсоқ жағдайлар, көптеген бақылауға алынбайтын факторлар әсер ететінімен түсіндіріледі. Сондықтан белгінің жалпы өзгергіштігін құрамды бөліктерге бөлу, қажеттілігі туындайды, бір жағынан нақты факторлармен анықталады, екінші жағынан бақылауға алынбайтын кездейсоқ себептермен туындайды. Көп факторлы дисперсиялық талдау Бұл бірнеше фактордың әсерін тек қана жеке емес, бірнеше фактор әсерін бірге де қарастырады. Ол толық күйінде дисперсиялық анализдің логикасына ешқандайда әсер етпейді,бірақ кейде процедура жүргізілуін қиындатады. Көпфакторлы дисперсиялық талдаудың бірфакторлы дисперсиялық талдаудан айырмашылығы: Бірфакторлы дисперсиялық талдау ANOVA 1.Дисперсиялық талдау бір шарт бойынша жүргізіледі; 2.ANOVA талдау жүргізу кезінде бір-бірден үш таңдама үшін қолданылады және олардың дисперсиясын салыстырады,қалыпты таралу заңы бойынша таралады. 3.ANOVA парамертлік мән болғандықтан,оны бас жиынтықтан аламыз. ANOVA бөлінеді: 1)парамертлік 2) параметрлік емес 4. Медицина мен биологияда бұл дисперсиялық талдаудың қателігі жиі кездеседі; Көпфакторлы дисперсиялық талдау MANOVA 1.Дисперсиялық талдаукем дегенде үш шарт бойынша жүргізіледі; 2.Бірінші шартқа ANOVA- ныңбір түрі немесе MANOVA- ның бір түрі әсер етеді. 3.Фактор ауырпалықтар қызметінде өлшеудің жеке шарттары қойылады. Мысалы:уақыттық,;ситуациялық;психологиялық; 4. Зерттеу нәтижесінде үш фактордан кем болмауы керек; Дисперсиялық талдау факторлар арасындағы өзара әрекеттесудің әсерін анықтауға және күрделі гипотезаларды тексеруге мүмкіндік береді. Өзара әрекеттесу терминін Фишер Фишерде алғаш рет 1926 ж. қолданды. Негізгі әсерлер өзара әрекеттесу эффектісі Екі топ студенттері бар делік, ал психологиялық тұрғыдан бірінші топтың студенттері берілген тапсырмаларды орындауға бейімделген және екінші топтың студенттеріне қарағанда мақсаттары айқын , ал екінші топ олар жалқау оқушылардан тұрады. Біз әр топты кездейсоқ екіге бөліп, әр топтың жартысынан қиын, ал екіншісінен жеңіл тапсырманы сұраймыз. Содан кейін біз оқушылардың бұл тапсырмаларды орындау барысында қаншалықты еңбек етіп жатқанын өлшейтін боламыз. Осы (ойдан шығарылған) зерттеудің орташа мәндері кестеде көрсетілген: Осы нәтижелерден қандай қорытынды шығаруға болады? 1) студенттер қиын тапсырманы орындау барысында көп жұмыс істейді; 2)мақсаттары айқын студенттер жалқау студенттерден көп жұмыс жасай ма? Бұл тұжырымдардың ешқайсысы кестеде көрсетілген орташа мәндердің жүйелік сипатының сипатын көрсетпейді. Нәтижелерді талдай отырып, тек мақсаттары айқын студенттер ғана қиын тапсырмаларды орындауда, ал жалқау оқушылар ғана жеңіл тапсырмалармен жұмыс істейді деп айту дұрысырақ болар еді. Басқаша айтқанда, оқушылардың табиғаты мен тапсырманың күрделілігі, бір-бірімен өзара әрекеттесу жұмсалған күшке әсер етеді. Бұл оқушылардың табиғаты мен тапсырманың қиындығы арасындағы жұптық өзара әрекеттесудің мысалы. 1 және 2-тұжырымдар негізгі әрекеттесу эффектілерін сипаттайды. Жоғары ретті өзара әрекеттесу. Жұптық өзара әрекеттесуді түсіндіру әлі де оңай болғанымен, жоғары деңгейлі өзара әрекеттесуді түсіндіру әлдеқайда қиын. Жоғарыдағы факторға тағы бір факторы енгізгеннен кейін: Енді осы алынған нәтижеге қарап мақсаты айқын әйелдер қиын тапсырманы жеңіл тапсырмадан гөрі қарқынды етеді. Ал ер адамда бұл керісінше болып тұр. Өзара әрекеттесуді сипаттаудың жалпы тәсілі. Жалпы, факторлар арасындағы өзара әрекеттесу бір эффектінің басқасының әсерінен өзгеруі ретінде сипатталады. Жоғарыда қарастырылған мысалда екі факторлы өзара әрекеттесуді сипаттайтын фактордың әсерінен проблеманың күрделілігін сипаттайтын фактордың негізгі әсерінің өзгеруі ретінде сипаттауға болады. Қорыта келсек, Дисперсияны талдау дисперсияны бөліктерге немесе компоненттерге бөлуге негізделген. Топішілік дисперсия топтау кезінде ескерілмеген факторлардың әсерін, ал топ аралық дисперсия топтастырушы факторлардың топтық ортаға әсерін түсіндіреді. Үш немесе одан да көп үлгілердің құралдарын салыстыру үшін бір факторлы дисперсия қолданылады.Кемшілігі: басқалардан ерекшеленетін үлгілерді бөліп алу мүмкін емес. Осы мақсатта Шефф әдісін қолдану керек немесе үлгілерді жұптық салыстыру жүргізу қажет. 31. Корреляциялық талдаудың негізі. Сызықты және сызықты емес корреляциялық тәуелділік. Медициналық-биологиялық ғылымда құбылыстар арасындағы байланыс өзге түрде – бір белгінің бір ғана шамасына екінші белгінің құбылмалы мәндер қатары сәйкес келетін байланыс тҥрінде анықталады. Мұндай байланыстар тірі табиғаттың әртүрлі құбылыстарының өзара әрекеттесуінің, алуан түрлілігінің нәтижесінде туады. Белгілер арасындағы бұл түрдегі байланысты корреляциялық (латынның correlation – өзара байланыс, өзара қатынас, орайластық деген мағыналарды білдіретін сөзінен шыққан) деп атайды. Корреляцилық талдау – бұл екі немесе одан көп кездейсоқ шамалардың арасындағы байланыстың тығыздығын және бағытын анықтайтын сандық әдіс. Корреляциялық талдау әр түрлі (өзгеретін) белгілер арасындағы тығыздықты немесе түйіндестік дәрежесін өлшеуге, сондай-ақ олардың арасындағы нысаны мен бағытын анықтайды Корреляциялық байланыс дегеніміз-бір белгінің өзгергіштігі екіншісінің өзгергіштігіне сәйкес келетіндігін көрсететін екі белгінің дәйекті өзгеруі. «Корреляция» терминін алғаш рет француз палеонтологы Ж. Кювье енгізді, ал статистикада оны Ф. Гальтон алғаш қолданды. Корреляциялық тәуелділіктерді зерттеу кестелік, графиктік және аналитикалық әдістермен жүргізіледі. Кестелік зерттеуде X және Y шамаларының арасындағы тәуелділік екі өлшемді кесте түрінде беріледі және ол корреляциялық тор деп аталады. Графиктік тәсілде координаталар жазықтығына (Х-абцисса, У-ордината) х және у шамаларының мәндеріне сәйкес келетін нҥктелер орналастырылады. Пайда болған нүктелер жиынтығын корреляциялық өріс деп атайды. Бағыты бойынша корреляциялық байланыс тура(оң) және кері(теріс) болып бөлінеді Тура корреляциялық байланыс – бір айнымалының артуы басқа айнымалының артуына (су құбырындағы судағы стандартты емес сынамалар артқан кездеде, іш сүзегімен аурудың артуы) байланысты болатын байланыс. Кері корреляциялық байланыс – бір айнымалының кемуі басқа айнымалының артуына («В» сарауруына қарсы екпе жұмысының ауқымын көбейткен сайын, онымен ауыратындардың кемуі) байланысты болатын байланыс. Корреляциялық байланыс Тура байланыс кезінде корреляция коэффициенті «0»-ден «+1»-ге дейінгі мәндерді қабылдайды. Кері байланыс кезінде корреляция коэффициенті «-1»-ден «0»-ге дейінгі мәндерді қабылдайды. Егер корреляция коэффициенті «0»-ге тең болса, онда құбылыстар арасында байланыс болмайды. Егер корреляция коэффициенті «+1» немесе «–1»ңболса, ондақұбылыстарарасындабайланысфункционалдықболады Аналитикалық байланыс бойынша сызықтық және сызықтық емес байланыстар ажыратылады: Егер құбылыстар арасындағы статистикалық байланысты шамамен түзудің теңдеуімен өрнектеуге болатын болса, онда оны түрдегі байланыс сызықтық байланысПирсонның корреляция коэффициенті деп атайды: y = a + bx. сызықтық түрдегі байланыс үшін корреляция коэффициенті (r): 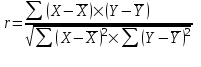 Егер байланысты кез-келген қисық сызықтың теңдеуімен (парабола, гипербола және т.б.) өрнектеуге болатын болса, онда мұндай байланыс сызықтық емес (қисық сызықты) байланыс деп аталады. сызықтық емес түрдегі байланыс үшін корреляциялық қатынаспен (ŋ): 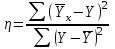 Сызықтық Корреляция коэффициентінің негізгі қасиеттері: -1≤ r ≤ 1, яғни r шамасы -1-ден кем және +1-ден артық бола алмайды, -1 және +1 сандары корреляция коэффициенті үшін шекаралар болып саналады. Егер есептеу барысында r шамасы -1-ден кіші немесе +1-ден үлкен болса, демек есептеуде қате кетті. Неғұрлым 1-ге жақын болса, х және у айнымалыларының арасындағы байланыс тығызырақ; Оның таңбасы байланыстың бағытын көрсетеді: - r>0 болғанда х және у айнымалыларының арасында тура корреляция бар; Егер r мәні 0,25 шамасынан аспаса, онда бұл таңдап алынған көрсеткіштер арасындағы байланысының әлсіз екендігін білдіреді. 0.25< r<0.3т аз тәуелділікте eгер 0,3< r<0,6 орташа байланыс тығыздығы r >0,6 байланыс тығыздығы жоғары Шашырау көп болса, y-тің x-тен Kорреляция тәуелділігі әлсіз болады немесе тіпті болмайды. Аз шашырау Kорреляция тәуелділігінің күшті, кей жағдайларда олардың арасында функциялық тәуелділік бар екендігін көрсетеді. Бірақ кейінгі жағдайда мұндай байланыс қосымша кездейсоқ факторлардың әсер етуінен жойылады r корреляция коэффициентін есептемейтін жағдайлар екі айнымалылар арасындағы байланыс сызықты емес, мысалы, квадраттық арақатынас; деректер әр айнымалы бойынша бірден көп бақылаулардан тұрады; бақылауда ауытқыған мәндер бар Корреляция коэффициентінің сенімділігі оны есептелетін орташа қателікпен салыстыру арқылы анықталады. Корреляция коэффициентінің орташа қателігі: анықтайды. mr √1 r^2 xy/ n 2 Егер корреляция коэффициенті орташа қателіктен 3 есе артық болса, онда сенімді деп есептелінеді. rxy корреляция коэффициентінің mr –орташа қателікке қатынасын сенімділік критериі деп атайды және t әрпімен белгілейді: t r xy/ mr Сызықтық корреляция мәнділігі жөніндегі жорамалды тексеру критерийі: Айталық, бізге екі сандық айнымалылардың арасында қандай да бір сызықты қатынастың бар – жоғын анықтау керек. Таңдама х және у шамаларының n тәуелсіз жұптарынан тұрады және ең болмағанда осы екі айнымалылардың біреуі қалыпты таралған. Нөлдік және балама жорамалдарды анықтаймыз: : Н0= (айнымалылар арасында корреляция жоқ); : Н1=(айнымалылар арасында корреляция бар). 2. Таңдама деректері бойынша r корреляция коэффициентін есептеу. 3. t статистикасын есептеу tстатистикасыеркіндікдәрежесіdf=n-2 сәйкескелетінСтьюденттіңtтаралуынабағынады. 4. Критерий статистикасыныңшамасынберілген α мәнділікдеңгейінесәйкескелетінtdf,αcынимәніменсалыстырады. Егерtбақ>tсыниболса, онда бас жиынтықтыңайнымалыларыарасындакорреляциялықбайланыстыңжоқтығы жөніндегі Н0 жорамалжоққашығарылады. Егер tбақ < tсыни болса, онда Н0 жорамалын жоққа шығаруға негіз жоқ. Спирменнің рангілік корреляция коэффициенті Пирсонның корреляция коэффициентінің параметрлік емес баламасы болып табылады. Ол таралудың қалыптылығын, сол сияқты сызықты тәуелділікті талап етпейді, оны сандық деректерге де, сапалық деректерге де қолдануға болады. Сонымен, егер келесі шарттардың біреуі немесе екеуі орындалса онда Спирменнің корреляция коэффициенті есептелінеді: -Деректер реттік, аралық немесе қатынас шкалаларында ұсынылуы мүмкін. -Х және У кездейсоқ шамаларын бөлудің кез-келген заңына жол беріледі. -Х және У кездейсоқ шамалары арасында монотонды өсетін немесе монотонды азаятын тәуелділік болуы керек. -Х немесе У айнымалыларының ең болмағанда біреуі рангілік шкалада өлшенеді. - Х айнымалысы да, У айнымалысы да қалыпты таралмаған. - Екі айнымалының арасындағы қатынас сызықты емес r 1 6 d^2/n( n^2 -1) Қорытыта келе, Корреляциялық (стохастикалық) байланыс – бұл жаппай бақылауда ғана байқалатын көрсеткіштердің арасындағы толық емес мүмкінді байланыс. Қос және көптік корреляцияны бөліп айтамыз. Корреляциялық қатынастарды зерттеу үшін келесі экономикалық зерттеудің тәсілдері қолданылады: қатарласқан және динамикалық қатарларды салыстыру, графиктер, аналитикалық топтастыру. Зерттелетін факторлар мен нәтижелік көрсеткіштердің арасындағы байланысты зерттеу үшін көп объектілерді алып, олардың мәндерін салыстырғанда шығады. Сонда үлкен сандар заңына сәйкес басқа факторлардың нәтижелік көрсеткішіне әсері жойлады. Бұлзерттелушіқұбылыстардыңарасындағықатынастықұруғамүмкіндікбереді. 32.Корреляциялық талдау.Параметрлер арасындағы байланыстың сипаттамасы және күші. Жалпы корреляциялық талдау дегеніміз -медициналық-биологиялық зерттеу жұмыстарының маңызды міндеттерінің бірі-зерттеліп отырған құбылыстарды немесе үрдістерді сипаттайтын белгілер арасындағы байланысты айқындау және өлшеу болып табылады. Корреляциялық талдауды не үшін қолданамыз-үйткені ол екі немесе бірнеше белгілердің арасындағы байланысты талдау үшін қолданамыз. Ал корреляциялық талдаудың негізгі міндетті-құбылмалы белгілердің арасындағы байланыстың бағытын оң немесе теріс,түрін яғни сызықты және сызықты емес анықтау, оның күшін,тығыздығын өлшеу және корреляциялық таңдама көрсеткіштерінің шынайлығын бағалау болып табылады. Сонымен қатар-айнымалылар арасында болатын байланыстар екі түрге бөлінеді олар: функционалдық байланыс және корреляциялық байланыс болып. Функционалдық байланыс деп-бір белгінің шамасының өзгеруіне екінші белгінің шамасының белгілі бір анықталған өзгеруі сәйкес келетін тәуелділікті айтамыз.Мұндай байланысқа мысалы ретінде:дөңгелектің ауданының оның радиусына тәуелділігін,жүрілген жолдың жылдамдық пен уақытқа тәуелділігін,сол сияқты химиялық реакциялардың жылдамдығының температураға тәуелділігін алуға болады. Ал корреляциялық байланыс деп-бір белгінің бір сандық мәніне екінші белгінің бірнеше мәні сәйкес келетін тәуелділікті айтамыз.Мысалы айтатын болсам:адамның бойының ұзындығын мен дене салмағының арасында оң байланыс бар екендігі белгілі, алайда бұл белгілердің мәндерінің арасында толық сәйкестік жоқ.Яғни бойларының ұзындықтары бірдей 160 см болсын,ал адамдардың әртүрлі дене салмақтары, 55,60,65 кг сәйкес келеді.Алайда дене салмағының бұл құбылмалылығы белгілі бір өлшемде өзінің орта шамасының айналасында өзгеріп түрленеді.Себебі адамдардың дене салмағы тек қана олардың бойларының ұзындықтарымен анықталмайды:оған көптеген басқа факторлар ықпал етеді,оның ішінде өмір сүру жағдайы,тамақтану түрі,спортпен шұғылдану және т.б болуыда мүмкін.Сондай-ақ сапалық белгілерде қатысады да және осыны байқауға болады:әдетте ақсары адамдардың көздерінің түсі көкшіл,қара торы адамдарда -қоңыр түсті болып келеді.Бірақтан қоңыркөзді ақсары адамдар мен көздері көкшіл түсті қараторы адамдарда кездеседі.Бұл биологиялық белгіге генетикалық та ,сыртқы факторларда ықпал ететіндігімен байланысты болып келеді. Параметрлер арасындағы байланыстың сипаттамасы және күші-Параметрлер арасындағы байланыс және корреляциялық байланыс-олар себепті-салдарлы тәуелділіктің айғағы ретінде қарастырылмайтынын есте сақтауымыз қажет және олар тек қана бір белгінің өзгеруіне екінші белгінің анықталған өзгерулері сәйкес келетінін көрсетеді.Корреляциялық әдісін қолданғанда әртүрлі белгілер арасындағы байланысты өлшеу тек қана сапа жағынан біртекті жиынтықтарда мүмкін екенін есте сақтауымыз маңызды.Мысалы жынысы және жас мөлшерлері әртүрлі адамдардың бойларының ұзындықтары мен дене салмақтарын салыстыруға болмайды. Сонымен қатар корреляциялық байланыстар-бағытты бойынша тура және кері корреляциялық байланыс деп бөлінеді. Тура корреляциялық байланыс-бір айнымалының артуы басқа айнымалының артуына яғни( су құбырындағы судағы стандартты емес сынамалар артқан кездеде,іш сүзегімен аурудың артуы)байланысты болатын байланыс. Кері корреляциялық байланыс-бір айнымалының кемуі басқа айнымалының артуына (“В” сарысуына қарсы екпе жұмысының ауқымын көбейткен сайын,онымен ауратындардың кемуі)байланысты болатын байланысты айтамыз. Тура корреляциялық байланыс кезінде- корреляция коэффициенті “0”-ден,”+1”-ге дейінгі мәндерді қабылдайды. Ал кері байланыс кезінде корреляция коэффициенті “-1”-ден “0”-ге дейінгі мәндерді қабылдайды. Қорытындылай келе: Корреляциялық талдауға анықтама берсем-бұл екі немесе оданда көп кездейсоқ шамалардын арасындағы байланыстың тығыздығын және бағытын анықтайтын сандық әдісті айтамыз. “Корреляция” терминін негізінен алғаш рет француз палеонтологы Ж.Кювье енгізді. Жоғарыда айтылғандай егер корреляциялық коэффициенті “ 0”-ге тең болса,онда құбылыстар арасында байланыс болмайды .Ал егерде корреляция коэффициенті “+1” немесе “-1” болса,онда құбылыстар арасында байланыс функционалдық болады.Сонымен қатар екі айнымалы арасындағы корреляциялық тәуелділікті көрсететін көрнекті әдіс бар яғни ол-шашырау диаграммасы деп аталады. Ал Пирсонның корреляциялық коэффициенті бойынша-сызықты (,жұптасқан Пирсонның )корреляциялық коэффициенті. Ол байланыстың күшін және бағытын сипаттайтын көрсеткіш болып табылады. r xy-дегеніміз корреляция коэффициентін айтамыз; x,y- корреляцияланатын қатар; x ,y- орташа шамаларды айтамыз. Пирсонның корреляция коэффициенті параметрлік коэффициент болып табылады. 33.Пирсонның корреляция коэффициенті және оның негізгі қасиеттері.Корреляция коэфициенттің мәнділікке тексеру.Сенімділік критерийі. Пирсонның корреляция коэффициенті - егер бір белгінің бір қалыпты өзгерулеріне екінші белгінің бір қалыпты яғни, өте аз ауытқулармен өзгерулері сәйкес келсе, онда байланыс түрі сызықты деп аталады. Яғни сызықты-бұл жұптасқан Пирсонның корреляция коэффициентін байланыстың күшін және бағытын сипаттайтын көрсеткішті айтамыз. Пирсонның корреляция коэфициенті параметрлік коэффициент болып табылады.Сонымен қатар Пирсонның корреляция коэффициенті сандық белгілердің сызықтық байланысын сипаттауға арналған және белгілердің қалыпты таралуын талап етеді.Оның бас жиынтықтағы ақиқат шамасы p таңдама r арқылы бағаланады. |
