2 ркк. 21. Сапалы белгілер арасындаы байланысты зерттеу. Орайласты кестелерін Xuквадрат критерийіні кмегімен талдау
 Скачать 273.69 Kb. Скачать 273.69 Kb.
|
|
Көптіклогистикалық регрессия екінемесеодан көп үздіксізнемесекатегориялықпредикторлықайнымалылар мен біркатегориялықтәуелдіайнымалыарасындағыбайланыстыбағалауүшінқолданылады. Медицинадакеңіненқолданылатынрегрессиялықталдаулардыңбіріжайсызықтырегрессиялықталдаудықарастырамыз. Сызықтырегрессиялықталдау Жайсызықтырегрессиялықталдаубірпредикторлықайнымалы мен біртәуелдіайнымалыарасындағыөзарабайланыстыңсызықтығынтексеруүшін, солсияқтыпредикторлықайнымалыбойыншатәуелдіайнымалыныңмәніналдын - ала болжауүшінқолданылады. Мысалы, оның көмегіменжас мөлшері мен холестерин деңгейініңарасындағыөзарабайланыстыбағалауғажәнежас мөлшерінебайланыстықандағыхолестеринніңдеңгейіналдын- ала болжауғаболады. Жайсызықтырегрессиялықталдауүшінекіүздіксізайнымалыларқажет. Олардыңбіреуіпредикторлық, екіншісітәуелдіболыпанықталады. Айталық, бізгеекіүздіксіз Х және У айнымалыларыныңарасындағыарақатынастызерттеуқажетболсын. Олүшінеңалдыментаңдамадағы n пациенттердіңәрқайсысыҥшін Х және У шамаларынөлшейміз. (Х,У) жұптарынасәйкес нүктелердіекіөлшемдішашылуграфигінеорналастырамыз. Егердеректердіңорналасуы түзусызықбойынажуықталса (аппроксимацияланса), ондаекіайнымалыарасындасызықтыарақатынасбар депайтамыз. Егербіз Y айнымалысы X айнымалысынантәуелдіжәне Y-тіңөзгеруі X-тіңөзгеруінебайланыстыдепсанасақ, онда Y-тің X-қарегрессиясынбағалаймыз. Яғни, бұл жағдайда X предикторлықайнымалы, Y тәуелді (жауапайнымалы) айнымалыболады. Белгілердіңөзарабайланысынтолықбағалауүшінекіжақты регрессия қарастырылады: Y-тіңөзгеруін X- тіңөзгеруібойыншабағалау (Y-тің X-қарегрессиясы) жәнекерісінше, X-тіңөзгеруін Y- тіңөзгеруібойыншабағалау (X-тің Y-қарегрессиясы). Екіжағдайда да есептеуәдісі мен ретіұқсасболғандықтанбіржақтырегрессияны, Y-тің X-керегрессиясынқарастыруменшектелеміз. Корреляциялықталдаужағдайындағыдай, кез-келгенрегрессиялық модель тек сандыққатынастардыанықтайалады, оларміндеттітүрдесебеп-салдарлыққатынастардыкөрсетпейді, яғни. бірфактордыңекіншіфакторғаәсері. Белгілердіңсебеп-салдарлықбайланысытуралыгипотезаларзерттелетінқұбылыстынемесепроцестімағыналытүрдетүсіндіреотырып, теориялықталдаукөмегіменқосымшанегізделуікерек. Алынғаннәтижелердітүсіндіру, яғни. оларды статистика тілінен экономика тіліненемесебасқапәнгеаудару - бұлрегрессиялықталдаудыңматематикалықжәнестатистикалықпроцедураларынқолданудангөріқиынкезең. 37. Регрессия теңдеуі. Регрессия параметрлері. Шашыраңқы диаграммасы. Y-тің X-қа регрессиясының теңдеуі деп X тәуелсіз айнымалысының мәндері мен Y тәуелді айнымалының шартты орта мәндерінің арасындағы тәуелділікті көрсететін yx=f(x) түріндегі теңдеуді айтады. Шартты орта мән деп X-тің нақты бір мәні үшін есептелген арифметикалық орта мәнін айтады. кезкелгенберілгенсалмақтыңмәніүшінәртүрлі бой ұзындықтарыкездеседі; бақыланған бой ұзындықтарыныңмәніберілгенсалмақтыңмәнінде, салмақ көрсеткішініңұлғаюынақарайөседі; бақыланғансалмақтыңмәндерінесәйкескелетін бой ұзындықтарының орта мәндері нүктелерініңгеометриялықорныбойдың (Y) салмақтан (X) регрессиялықтәуелділігідепаталады. Сызықты регрессия теңдеуі Регрессия сызығы: Y=a+bX түріндегі түзудіңтеңдеуімен (немесе «моделімен») сипатталады, мұндағы Y-тәуелдіайнымалыныңболжанатынмәні, a-бос мүше, регрессия сызығының Y осіменқиылысу нүктесі, b-регрессия сызығының бұрыштықкоэффициенті, оны әдеттерегрессия коэффициентідепатайды, ал X- предикторлықайнымалы, оның көмегімен Y мәніболжанады. X предикторлықайнымалысыныңберілгенмәнібойынша Y-тіңсәйкесмәнінесептеугеболады. Сонымен, Y-тің мүмкінмәнінзерттеліпотырғанауқымныңшекарасында X-тіңкезкелгенмәніүшіналдын-ала болжауғаболады. Регрессия коэффициентінің (b) үлкенстатистикалықмәні бар: олX предикторлықайнымалыбірбірліккеөзгергенсайын Y жауапайнымалының орта мәніқаншашамағаөзгеріпотыратынынкөрсетеді. Мысалы, адамныңденетемпературасы 1оС көтерілгендетамырсоғуыжиілігіорташаалғандаминутына 10 соққыға көбейеді. Еңкішіквадраттарәдісі Бізрегрессиялықталдаудытаңдамабақылаунәтижелерібойынша жүргіземіз, сызықты регрессия теңдеуіндегіa жәнеbкоэффициенттері бас параметрлердің (сәйкесaжәнеb) таңдамабағалары. а жәнеbпопуляциядағысызықтырегрессияныңсызығынанықтайды. Бақылаунәтижелерібойыншамодельдіңпараметрлерінанықтауүшін еңкішіквадраттарәдісіқолданылады. Бұл әдісбойыншаа жәнеb коэффициенттеріyiбақыланғанмәндерініңәрқайсысыныңрегрессияның түзусызығындағысәйкесмәндерденауытқуларыныңквадраттарыныңқосындысымейлінше аз болатындайетіптаңдалынады. Сызықтықрегрессиядақолданылатынрегрессиясызығыәдеттееңкішіквадраттарсызығыболыптабылады, яғни, ең кішіквадраттарәдісінесәйкес 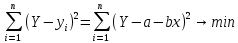 болуыкерек. Аргументтеріа жәнеb болатын осы функцияныңтуындыларынқолданыпэкстремумғазерттеунәтижесіндееңжақсыа жәнеbкоэффициенттерініңформулаларыналамыз: B=∑((xi-x)*(yi-y))/∑(xi-x)^2немесе b=(xy- x*y)/(x^2-(x)^2) Сызықтырегрессиялықталдаужҥргізуҥшінайнымалылармәндері төмендегішарттардықанағаттандыруытиіс: X пен Y сызықтыбайланысқан; Таңдамадағыбақылауларбір - бірінентәуелсіз. Бақылаулартәуелсізболуыүшінәрбір пациент бойыншабақылау жұбы бір-ден көп емес; X әрбіршамасыүшінпопуляциядаyшамасыныңтаралуы бар жәнеолтаралуқалыпты. Y шамаларының бұл таралуларының орта мәніпопуляцияның регрессия сызығындажатады. X шамаларыныңбарлығыүшінпопуляцияда Y шамаларыныңдисперсиясы (σ2) бірдей. Регрессия теңдеуініңкоэффициенттерініңмәнділігінбағалау Регрессия теңдеуініңкоэффициенттері (a және b) көлемішектеулітаңдамадеректерібойыншаесептелгендіктенолардыңмәнділігінбағалауқажет. Егер регрессия теңдеуінің a және b коэффициенттерініңекеуі де мәндіболса, ондатеңдеуақырғытеңдеудепаталады. Егеркоэффициенттердіңарасындамәндіемесі бар болса, ондаол параметр теңдеуденалыныптасталады. I. Регрессия коэффициентінің (b) мәнділігінбағалау 1. Нөлдікжәнебаламажорамалдардыанықтаймыз: H0: бас жиынтықта (популяцияда) айнымалыларарасындағыбайланыстыңсипатырегрессиялықемес, яғни b=0 H1: бас жиынтықта (популяцияда) айнымалыларарасындағыбайланыстыңсипатырегрессиялық, яғни b≠0 2. Критерий статистикасынесептейміз: tбақылау=|b|/Sb еркіндікдәрежесінің саны df=n-2 теңСтьюденттің t таралуынабағынады, мұндағыSb - b коэффициентініңстандарттыққатесі. Sb=σ2/ 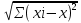 σқалдықшамасықалдықстандарттықауытқудепаталады (сәйкес, σ2қалдық=∑[Y-(a+bx)]/(n-2) қалдық дисперсия) σқалдық тәуелді және тәуелсіз айнымалылардың σx, σy стандарттық ауытқуларымен байланысты σқалдық= 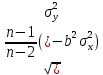 формуласымен анықталады. Мұндағы: формуласымен анықталады. Мұндағы:σx= 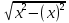 , σy= , σy=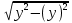 Сонымен, Sb= 1/ 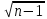 *(σ2қалдық /σx) *(σ2қалдық /σx)3. Стьюдент таралуыныңсынимәндерікестесіненберілгенмәнділікдеңгейінежәнеdf=n-2 сәйкесta, dfсынимәнінтабамыз. Егер|tбақылау|>tсыниболса, ондаP<α, нөлдікжорамалжоққашығарылады, яғни бас жиынтықтаекіайнымалыарасындағыбайланысстатистикалықмәнді(b≠0). 4. Нәтижелергеқорытындыжасау. II. Регрессия теңдеуінің бос мүшесіa коэффициентінмәнділіккетексеруүшінt=|a|/Saстатистикалықкритерийіқолданылады. t – еркіндікдәрежесіdf=n-2болатынСтьюденттіңt таралуынабағынады. МұндағыSa-a коэффициентініңстандарттыққатесі. Sa=σқалдық 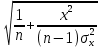 формуласымен есептеледі. формуласымен есептеледі. Әріқарайесептеулерb коэффициентіүшінжасалғанесептеулергеұқсас. αкоэффициентіҥшін 95% сенімаралығы: a-t0.05Sa түріндеанықталады. Регрессиятеңдеуініңсапасынбағалау Таңдамабақылауларнегізіндеалынғанрегрессиятеңдеуініңбасжиынтықтағыақиқатрегрессиятеңдеуінесәйкестігінтексеруүшінжұптасқантаңдамалардыңортамәндерінбағалауғаарналғанайырмаларәдісінқолдануғаболады. tбақылау=d/Sd мұндағыd=(Yбақ-Yтеор), Yбақ- бақыланғанмәндер, Утеор- регрессиятеңдеуібойыншаесептелгентеориялықмәндер). d=∑(Yбақ-Yтеор)/n Sd=σ/(n-1), σ= 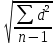 Егерtбақ Корреляция немесешашыраңқы графикадегеніміз - шамаларарасындағыбайланыстыанықтауүшінбайланыстыайнымалылардыңөзарабайланысыныңграфикалықкөрінісі. Соныменқатар, тәуелді x айнымалысыөзгергенкездетәуелді у өзгермелімәніқалайөзгеретініайқынболады. Корреляциялық диаграмма - бұлекінемесеодан да көпөзгеретінфакторларарасындағыстатистикалықбайланыстыолардыңмәндеріарасындағыбайланыстыорнатуүшінграфикалықтүрдекөрсету. Диаграммада «температура» және «ені» екіатрибуттыбілдіретіннүктелер бар. Позитивті корреляция дегеніміз - температура неғұрлымжоғарыболса, ені де соғұрлымкөпболады. Теріс корреляция керібайланыстыұсынады: температура неғұрлымжоғарыболса, енісоғұрлым аз болады. 38. Ең кіші квадраттар әдісі бойынша сызықты регрессия параметрлерін бағалау. Регрессиялық талдау(regression analysis) – бұл бір тәуелді айнымалы мен бір немесе бірнеше тәуелсіз айнымалылар арасындағы статистикалық өзара байланысты зерттеу әдісі. Регрессиялық талдауда тәуелсіз айнымалыны предиктор (ағыл.predictor - болжамшы), тәуелді айнымалыны «жауап айнымалы» деп атайды. Регрессиялық талдау – жауап айнымалының (тәуелді) мәнін бір немесе бірнеше (тәуелсіз) предикторлық айнымалылардың белгілі мәндері бойынша алдын - ала айтуға немесе бағалауға мҥмкіндік беретін статистика бөлімі. Тәуелді айнымалының орта мәні мен предикторлардың орта мәндері арасындағы өзара байланыс регрессия теңдеуі түрінде өрнектеледі. Регрессия теңдеуі - тәуелді айнымалы мен предикторлық айнымалылардың бастапқы статистикалық деректері негізінде таңдалынып алынатын математикалық функция. Көбінесе сызықты функция қолданылады. Бұл жағдайда регрессиялық талдау сызықты регрессиялық талдау деп аталады. Ең кіші квадраттар әдісі бойынша регрессиялық талдауды таңдама бақылау нәтижелері бойынша жүргіземіз, сызықты регрессия теңдеуіндегі a және b коэффициенттері бас параметрлердің (сәйкес a және b) таңдама бағалары. a және b популяциядағы сызықты регрессияның сызығын анықтайды. Ең кіші квадраттар әдісі — математикалық статистиканың аса маңызды бір бөлімі және ол статистика қорытынды жасау үшін ғылым мен техниканың әр түрлі саласында кеңінен қолданылады. Гаусс бойынша, Регрессиялық талдауды таңдама бақылау нәтижелері бойынша жүргізеді, сызықты регрессия теңдеуіндегі a және b коэффициенттері бас параметрлердің сәйкес a және b таңдама бағалары. A және b популяциядағы сызықты регрессияның сызығын анықтайды. Бақылау нәтижелері бойынша модельдің параметрлерін анықтау үшін ең кіші квадраттар әдісі қолданылады. Бұл әдіс бойынша а және b коэффициенттері yi бақыланған мәндерінің әрқайсысының регрессияның түзу сызығындағы сәйкес мәндерден ауытқуларының квадраттарының қосындысы мейлінше аз болатындай етіп таңдалынады. Сызықтық регрессияда қолданылатын регрессия сызығы әдетте ең кіші квадраттар сызығы болып табылады, яғни, ең кіші квадраттар әдісіне сәйкес болуы 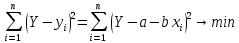 керек. Барлық қателердің квадраттарының қосындысыең кіші болатындай етіп, регрессия теңдеуін шығару ЕККӘ мәні болып табылады. Аргументтері а және b болатын осы функцияның туындыларын қолданып экстремумға зерттеу нәтижесінде ең жақсы а және b коэффициенттерінің формулаларын аламыз: 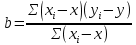 немесе немесе 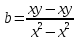 Сызықты регрессиялық талдау жүргізу үшін айнымалылар мәндері белгілі бір шарттарды қанағаттандыруы тиіс: X пен Y сызықты байланысқан; Таңдамадағы бақылаулар бір - бірінен тәуелсіз. Бақылаулар тәуелсіз болуы үшін әрбір пациент бойынша бақылау жұбы бір-ден көп емес; X әрбір шамасы үшін популяцияда У шамасының таралуы бар және ол таралу қалыпты. Y шамаларының бұл таралуларының орта мәні популяцияның регрессия сызығында жатады. X шамаларының барлығы ҥшін популяцияда Y шамаларының дисперсиясы σ2 бірдей. Регрессиялық талдаудың негізгі мәселесі b0 мен b1 тұрақты коэффициенттерінтабу жәнеолардың статистикалық маңызын бағалау. Шашырау диаграммасындағы нүктелер арқылы бірнеше түзу сызықтарды жүргізуге болады, олар бір-бірінен b0 және b1 коэффициенттерімен өзгешеленеді. Олардың ішінен Y пен X арасындағы байланысты ерекше сипаттайтынын таңдау қажет. Мұны жасаудың тәсілдерінің бірі-ең кіші квадраттар әдісін қолдану. Сызықты регрессия параметрлерін ең кіші квадраттар әдісі бойынша бағалау Регрессия теңдеуін құру, оның коэффициенттерін (параметрлерін) бағалауға алып келеді, ол үшін ең кіші квадраттар әдісі қолданылады. Ең кіші квадраттар әдісі: болғанда параметрлерді бағалауға мүмкіндік береді. Ең кіші квадраттар әдісі бойынша сызықты регрессия у=a+bхтеңдеуінің параметрлерін анықтау формуласы: 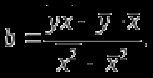 Регрессия коэффициентінің маңыздылығын тексерудің сызбасы 1) Н0:a=0, b=0. Н1: a≠0, b≠0. 2) р=0,05 – маңыздылық деңгейі. 3) 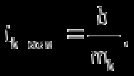 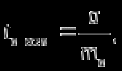 мұндағы mb, ma - кездейсоқ қателіктер: 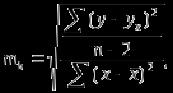 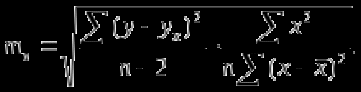 4) tкесте(р; f), мұндағы f=n-k-1, n - бақылау саны, k - айнымалылары «х» теңдеудегі параметрлер саны. 5) Егер болса, ондаН0қабылданбайды, яғни коэффициент маңызды. Егер болса, ондаН0қабылданады, яғни коэффициент маңызды емес. Регрессия теңдеуінің маңыздылығын тексерудің сызбасы 1) Н0: регрессия теңдеуі маңызды емес. Н1: регрессия теңдеуі маңызды. 2) р=0,05 – маңыздылықдеңгейі. 3) 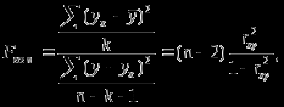 мұндағыn- бақылау саны; k - айнымалылары «х» теңдеудегі параметрлер саны; у - нәтижелі белгінің нақты мәні; yx- нәтижелі белгінің теориялық мәні; - жұпталған корреляция коэффициенті. 4) Fкесте(р; f1; f2), мұндағы f1=k, f2=n-k-1- еркіндік дәрежелерінің саны 5) ЕгерFесеп>Fкесте, онда регрессия теңдеуі дұрыс таңдалған. ЕгерFесеп 39. Регрессия коэффициенттінің мәнділігін тексеру жорамалы. |
