2 ркк. 21. Сапалы белгілер арасындаы байланысты зерттеу. Орайласты кестелерін Xuквадрат критерийіні кмегімен талдау

• Название: 21. Сапалы белгілер арасындаы байланысты зерттеу. Орайласты кестелерін Xuквадрат критерийіні кмегімен талдау
• Дата: 03.05.2022
• Размер: 273.69 Kb.
• Имя файла: 2 ркк.docx
• Тип: Документы; #510020
• страница: 4 из 6

Корреляциялық коэффициенттің негізгі қасиеттері:

- r шамасы -1-ден кем және +1-ден артық бола алмайды;

-1және +1 сандары корреляция коэффициенті үшін шекаралар болып саналады.Егер есептеу барысындағы r шамасы -1-ден кіші немесе +1 ден үлкен болса ,демек есептеуде қате кетті деген сөз. r неғұрлым 1-ге жақын болса, соғұрлым x және y айнымалыларының арасындағы байланыс тығызырақ болады;

Және оның таңбасы байланыстың бағытын көрсетеді:

-r 0 ден үлкенболғанда x және yайнымалыларының арасында тура корреляция бар;

-r 0 ден кіші болса ,кері корреляция бар. Оның шамасы нүктелердің түзу сызыққа қаншалықты жақын орналасқанын көрсетеді,яғни корреляция байланыстың күшін сипаттайды:

- r 0.3 тен кіші болғанда әлсіз болады,

- Ал 0,3 тен үлкен, 0,7 ден кіші - болса орта,

- 0,7 ден үлкен болса - күшті байланыс.

- Ал 0 ге тең болғанда сызықты корреляция жоқ дегенді білдіреді.

- корреляция коэффициентінің өлшем бірлігі жоқ.

- х және у айнымалыларының арасындағы корреляция міндетті тҥрде себептер мен салдарлар қатынасын білдірмейді;

- х пен у бір – бірін алмастыра алады, бұл жағдайда r мәні өзгермейді: ;

r2 шамасы детерминация коэффициенті деп аталады. Ол байланыс дәрежесін сипаттайды.

Корреляция коэфициенттің мәнділікке тексеру үшін:

1.Ең алдымен, нөлдік және балама жорамалдарды анықтаймыз.

Но: р тең 0, айнымалылар арасында корреляциялық байланыс жоқ.

Н1: р тең емес 0, айнымалылар арасында корреляциялық байланыс бар.

2.Таңдама деректері n саны бойынша таңдама корреляция коэффицентін, яғни r ді есептейміз. Формула боәынша есептеу оңай болу үшңн, кестеге белгілеп, х у орта мән мен таңдаман мәндерді есептеп аламыз.

3.Корреляция коэффициентінің орташа қателігін анықтаймыз, оны mr мен белгідейді.

4.Сенімділік критериін анықтаймыз, t

5.t – ді ta, df мәнімен салыстырып, a=0,05 алынған сенім интервалыдағы Стьюдент критерийінің критикалық мәні және еркіндік дәрежесі df=n-2.

6. Қорытынды жазамвз. Қорытынды 3 рет жазылады. 1 ші қорытынды корреляция коэффициенті туралы болса, 2 ші қорытынды қай жорамал қабылданатындығы туралы, ал 3 ші қорытынды бсцланыс дәрежесі турплы.

Корреляция коэффициентінің сенімділігі оны есептелетін орташа қателікпен салыстыру арқылы анықталады.

Корреляция коэффициентінің орташа қателігі: mr мен белгіленеді. Егер корреляция коэффициенті орташа қателіктен 3 есе артық болса, онда сенімді деп есептелінеді. Олай болмаса бақылау санын көбейту керек.

Корреляция коэффициентінің сенімділік бағасы:

- rxy корреляция коэффициентінің оның mr орташа қатеге қатынасы tr әріпімен белгіленіп нақтылық критерийі деп аталады. Егер tr 3 тен үлкен немесе тең болса, онда жеткілікті үлкен сан өлшеулерде корреляция коэффициенті нақты болып табылады.

- Алынған эмпириялық корреляция коэффициенті Пирсон корреляция коэффициентінің қималы мәндер кестесінен табылған қималы мәнімен салыстырылады, сонымен қатар еркіндік дәрежелерінің санын k = n – 2 формуласымен табады, мұндағы n-таңдама көлемі.

- Егер есептелген корреляция коэффициентінің шамасы rэмпре - rсыни мәннен үлкен болса, онда Но: нөлдік жорамал: қабылданады.

• Егер есептелген корреляция коэффициентінің шамасы rэмп≥rкрит, онда Но: нөлдік жорамал қабылданбайды. Н1:балама жорамал әділетті.

Қорыта келгенде:

Пирсонның корреляция коэффициенті - бір белгінің бір қалыпты өзгерулеріне екінші белгінің бір қалыпты яғни, өте аз ауытқулармен өзгерулері сәйкес келсе, онда байланыс түрі сызықты деп аталуын ацтамыз. Ол екі сандық кездейсоқ шамалар арасындағы байланысты зерттеу үшін қолданылады, мысалы, салмақ пен бойы арасындағы байланыс.Корреляциялық коэффициенттің негізгі қасиеттері бар, солар арқылы есептің дұрыс және нақты шешімін біле аламыз. Корреляция коэфициенттің мәнділікке тексеру үшін, белгілі бір алгоритмдерді орцндпу қажет. Корреляция коэффициентінің сенімділігі оны есептелетін орташа қателікпен салыстыру арқылы анықталады, оны mr арқылы белгілецміз. Егер корреляция коэффициенті орташа қателіктен 3 есе артық болса, онда сенімді деп есептелінеді, олай болмаған жағдайда бақцлау мәнге көбецтеміз.

34. Рангті корреляция. Спирменніңрангілік корреляция коэффиценті.

Жалпыкорреляциялықталдау-бұлекінемесеоданкөпкездейсоқшамалардыңарасындағыбайланыстыңтығыздығынжәнебағытынанықтайтынсандықәдісболыптабылады. Корреляциялықбайланыс- бағытыбойынша 2-ге бөлінеді: тура жәнекерікорреляциялықбайланысдеп.

Тура корреляциялықбайланыс – бұлбірайнымалыныңартуыбасқаайнымалыныңартуынабайланыстыболатынбайланыстыатаймыз, ал керікорреляциялықбайланысдеп- бірайнымалыныңкемуібасқаайнымалыныңартуынабайланыстыболатынбайланысболыптабылады. 1904 жылыағылшынпсихологы, Лондон және Честерфилд университеттерінің профессоры Чарльз Эдвард Спирманкорреляциялықталдаужасауүшінбұлкритерийдіұсынған.

Рангті корреляция коэффициенті – бұләртүрлібелгілердіңберілгеннұсқасындағышендердіңарасындағыбайланыстыөлшейтін коэффициент болыптабылады. Рангті корреляция коэфиценті - Ранжирлеугежататынмәндердің 2 қатарыболғанкездеқолданыладыжәнеәрбелгіүшінжеке-жекекөрсеткіштердіранжирлеуді

қамтып, еңкішімәнге-еңкіші ранг беріледі. Соныменқатар, зерттелетінқұбылыстардыңбайланысынанықтауғаарналғанпараметрлікемесстатистикалықәдіскежатады.Осы критерий арқылысандықмәліметтердің 2 қатарарасындағыбайланыстыанықтауарқылысандықтүрдекөрсетілгенанықталғанбайланыстыңтығыздығынбағалаймыз.

Спирменніңрангілік корреляция коэффициентіПирсонның корреляция коэффициентініңпараметрлікемесбаламасыболыптабылады. Бұлтаралудыңқалыптылығын, солсияқтысызықтытәуелділіктіталапетпейді, оны сандықдеректерге де, сапалықдеректерге де қолдануғаболады. Сонымен, егердебірқатаршарттардыңбіреуінемесеекеуіорындалсаондаСпирменнің корреляция коэффициентіесептелінеді:

- Х немесе У айнымалыларыныңеңболмағандабіреуірангілікшкаладаөлшенеді.

- Х айнымалысы да, Уайнымалысы да қалыптытаралмаған.

- Таңдамакөлеміүлкенемес.

- Екіайнымалыныңарасындағықатынассызықтыемес.

Спирменніңрангілік корреляция коэффициенті: кездейсоқшаманыңтарамдалузаңыбелгісізнемесеолқалыптыжағдайға сай болмасажәнесандықемесбелгілерменжұмысістесек (мысалы, сапалықбелгілермен) осы К.Спирменрангтеркорреляциясыныңкоэффициентіқолданамыз. Алдын ала әрбірбелгігежеке ранг беріледі. Рангілердіқоюкезіндемәнібойыншатеңшамалардыңрангісі, оныңранжирленгенқатардағынөмерлерініңарифметикалықортасынатеңекенінескерукерек. Толықбайланыскезіндебелгілеррангтерітеңеседі, жәнеолардыңайырмасы 0-ге теңболады, сәйкесінде корреляция коэффициенті 1-ге теңболады. Егербелгілертәуелсізөзгеріпотырса, корреляция коэффициенті 0-ге теңболады.

Спирменкорреляциясыныңкоэффициентініңмәнділігітуралыболжамдытексеруүшінкритикалықмәндеркестесінқолдануғаболады.Егересептелген корреляция коэффициентікестелікмәнненжоғарыболса, ондашамаларарасындағыбайланысстатистикалықмәнділікболады.

Спирменніңрангілік корреляция коэффициентініңформуласы: р= 1–6/n3 – n(rx-ry)2.

Орындауалгоритмі:

1. Н0 нөлдікжәне Н1 баламажорамалдардыанықтаймыз.

2.Рангілік корреляция коэффициентіrsесептейміз.

3.Корреляция коэффициентініңстатистикалықмәнділігінтексереміз.

4. Қорытындыжазамыз.

Қорытындылай келе: «Корреляция» терминіналғашрет француз палеонтологы Ж. Кювье енгізгенболатын, ал статистикада оны Ф. Гальтоналғашқолданғанболатын. Бағытыбойынша тура жәнекерікорреляциялықбайланысдепбөлінеді .Шашыраудиаграммасыяғни у жәнех өсіндеорналасуынбайланыстыбайланыстартүзетжалпыламасипатамалардыңүштүрі бар ол тура байланыс , керібайланысжәне тура , байланысжоқжалпылыматолықсипатамаладыжоғарыданегізгіолдатолықсипаттапөтетінболатынмын, әріқаратажүрсекбіздегі осы байланыстардыңнегізгіқабылдайтынмәндеріболадыяғни «+», «-» мәндері . Яғнибізбілемізқайтұстақандаймәндердіқабылдайтынымызды . Лондон және Честерфилд университеттерінің профессоры Чарльз Эдвард Спирменніңкорреляциялықталдаужасауүшінбұлкритерийдіұсынғанболатын .

Жалпыбірсөзбентүйіндейкеллсемөзмамандығымызда да жәнедебасқадамамандықтардадарангті корреляция кеңіненқолданыстажәнеде ары қарайдамыйбереді.

Сонымен қатар спирменнің шендік корреляция әдісіні-ранжирлеуге жататын 2-қатары болған кезде, қолданылады және әр белгі үшін жеке-жеке көрсеткіштерді ранжирлеуді қамтиды,және ең кіші мәнге-ең кіші ранг беріледі.Зерттелетін құбылыстардың байланысын анықтауға арналған параметрлік емес статистикалық әдіске жатады,сандық мәліметтердің 2-қатар арасындағы байланысты анықтайд.Сандық түрде көрсетілген анықталған байланысының тығыздығын бағалау.

Спирмен критерийі бойынша корреляциялық талдау алгоритмі бойынша:

1.Жұптастырылған салыстырмалы белгілер 2 қатарға орналастырылады, олардың біреуі Х, ал екіншісі Y арқылы белгілейді.

2.Х қатарының мәндері өсу немесе кему ретімен орналастырады.

3.Y қатарының мәндерінің орналасу реті олардың Х қатарының мәндеріне сәйкестігі арқылы анықталады.

4.Х қатарындағы әр мән үшін рангті анықтаймыз-минимумнан максимумға дейін реттік нөмір тағайындалады.

5.Сондай-ақ Y қатарындағы әрбір мәнге рангті анықтау минималды мәннен максимумға дейін.

6.D=X-Y формуласына жүгіну арқылы XжәнеY қатарлары арасындағы айырмашылықтыD есептеу.

7.Алынған айырмашылық мәндерін квадраттау.

8.Квадратталған айырмашылық мәндерін қосу.

9.Есептеулерді формула бойынша орындау.

Спирменнің шендік корреляциялық коэффициенті бар, шендік корреляция коэффициенті- бұл әр түрлі белгілердің берілгені нұсқасындағы шендердің арасындағы байланысты өлшейтін коэффициент болып табылады.

35. Спирменнің рангілік корреляция коэффицентінің қасиеттері және корреляция коэффициентінің мәнділігі жөнінде жорамалды тексеру.

Спирменнің рангілік корреляция коэффициенті - құбылыстар арасындағы байланысты статистикалық зерттеу үшін қолданылатын параметрлік емес әдіс. Бұл жағдайда зерттелетін белгілердің екі сандық қатарлары арасындағы параллелизмнің нақты дәрежесі анықталады және сандық көрсетілген коэффициенттің көмегімен белгіленген байланыстың тығыздығына баға беріледі.

Спирменнің рангілік корреляция коэффициенті Пирсонның корреляция коэффициентінің параметрлік емес баламасы болып табылады. Ол таралудың қалыптылығын, сол сияқты сызықты тәуелділікті талап етпейді, оны сандық деректерге де, сапалық деректерге де қолдануға болады. Сонымен, егер келесі шарттардың біреуі немесе екеуі орындалса онда Спирменнің корреляция коэффициенті есептелінеді:

• 
  Х немесе У айнымалыларының ең болмағанда біреуі рангілік шкалада өлшенеді.
  
• 
  Х айнымалысы да, Уайнымалысы да қалыптытаралмаған.
  
• 
  Таңдама көлеміүлкенемес.
  
• 
  Екіайнымалыныңарасындағықатынассызықтыемес.
  

Спирменніңдәрежелік корреляция коэффициентісалыстырылғансандықкөрсеткіштердіңекісериясыарасындағытәуелділіктіңтығыздығынанықтаужәнебағалауүшінқолданылады. Көрсеткіштерқатарыныңжоғарылаунемесетөмендеудәрежесібойыншареттелгенжағдайларыкөпжағдайдасәйкескеледі (біркөрсеткіштіңүлкенмәнібасқаиндикатордыңүлкенмәнінесәйкескеледі - мысалы, науқастыңбойы мен оныңденесінсалыстырғанкездесалмақ), тікелей корреляция бар дегенқорытындыжасалады. Егеркөрсеткіштердіңқатарларықарама-қарсыбағытқаиеболса (біркөрсеткіштіңүлкенмәніекіншісініңкішімәнінесәйкескелсе - мысалы, жас пен жүрексоғужиілігінсалыстырғанкезде), ондаоларкөрсеткіштерарасындағыкерібайланыстуралыайтады.

Спирменнің корреляция коэффициентікелесіқасиеттергеие:

• 
  Корреляция коэффициентімәндерді минус біреуіненекіншісінедейінқабылдайалады, ал r_s = 1 кезіндеқатаңтікелейбайланыс, ал r_s= -1 кезіндеқатаңкерібайланысболады.
  
• 
  Егер корреляция коэффициентітерісболса, ондакерібайланысболады, егеролоңболса, ондатікелейбайланысболады.
  
• 
  Егер корреляция коэффициентінөлгетеңболса, ондашамаларарасындаісжүзіндебайланысболмайды.
  
• 
  Корреляция коэффициентініңмодулібіреуінежақынболғансайын, өлшенетіншамаларарасындағыбайланыскүштірекболады.
  

Спирменнің бас жиынтықүшінрангілік корреляция коэффициентініңρ_sшамасынr_sтаңдамамәнібойыншабағалау

1. Х шамасыныңмәндерінөсу ретіменорналастырып, еңкішішамасынанбастапрангтерберіледі (1,2,3... n нөмірлері). Теңшамаларғаолартеңболмағанжағдайдаберілетінрангтердің орта мәніберіледі. Мысалы 1, 4, 8, 8,12 қатарында төртсаныныңрангі 2, ал 8 саныныңрангі 3,5 тең.

2. Осындай түрде У шамасыныңмәндеріранжирленеді.

3. Х және У шамаларыныңмәндерініңорнынаолардыңрангтеріналыпПирсонның корреляция коэффициентінесептейді.(r_s – х және у рангілерініңарасындағыПирсонның корреляция коэффициенті), немесе оны

r_s=1-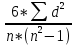

формуласыменесептеугеболады.

Мұндағы d-таңдаманыңәрбір мүшесіүшінрангілердіңайырмасы.
Спирменніңрангілік корреляция коэффициентініңқасиеттеріжәне корреляция коэффициентініңмәнділігі жөніндежорамалдытексеру

Спирменніңрангілік корреляция коэффициентініңқасиеттеріПирсонның корреляция коэффициентіүшінанықталғанқасиеттерменбірдей (r-діr_s-кеауыстырады). Алайда:

1. 
   r_s Х және У арасындағыбайланыстың (сызықтыболуыміндеттіемес) өлшемінбереді.
   
2. 
   r_s²есептелмейді
   
3. 
   р_s = 0 нөлдікжорамалдытексеруүшін:
   

- егертаңдама көлемі n≤50 болса, ондаСпирменнің корреляция коэффициентініңсынимәндеріанықталғанарнайыкестеніқолданамыз. Нөлдікжорамалдыжоққашығаруүшінr_sбақ>r_sсыниболуықажет;

- егертаңдама көлемі n>50 болса, онда Стьюдент критерийінқолдануқажет:

t_бақ= 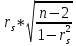, df=n-2

Коэффициентпараметрлікеместалдауәдісіболғандықтан, қалыптыүлестірудітексеруқажетемес.

Салыстырмалыиндикаторлардыүздіксізшкалабойыншада (мысалы, 1 мклқандағыэритроциттердіңсаны), сондай-ақреттік (мысалы, сарапшылардыңбағалаунәтижелері 1-ден 5-ке дейін) бойыншадаөлшеугеболады.

Кез-келгенөлшенетіншамалардыңәртүрлімәндерініңарасындағыайырмашылықжеткіліктіүлкенболса, Spearman бағалауыныңтиімділігіменсапасытөмендейді. Егерөлшенгеншамалардыңбіркелкіеместаралуыболса, Спирменкоэффициентінқолдануұсынылмайды.

36. Регрессиялық талдаудың негізгі түсініктер және әдістері. Регрессиялық талдау моделдері.

Регрессиялық талдау - бұл айнымалылар арасындағы байланысты бағалаудың статистикалық әдістерінің жиынтығы. Оның көмегімен айнымалылар арасындағы байланыс дәрежесін бағалауға және болашақтағы тәуелділіктерді модельдеуге болады. Шын мәнінде, регрессия әдістері «тәуелді айнымалының» өзгеруін ұстап алу үшін «тәуелсіз айнымалылардағы» өзгерістерді қалай қолдануға болатындығын көрсетеді.

Регрессиялық талдау(regression analysis) – бұл бір тәуелді айнымалы мен бір немесе бірнеше тәуелсіз айнымалылар арасындағы статистикалық өзара байланысты зерттеу әдісі. Регрессиялық талдауда тәуелсіз айнымалыны предиктор (ағыл.predictor - болжамшы), тәуелді айнымалыны «жауап айнымалы» деп атайды.

Регрессиялық талдау – жауап айнымалының (тәуелді) мәнін бір немесе бірнеше (тәуелсіз) предикторлық айнымалылардың белгілі мәндері бойынша алдын - ала айтуға немесе бағалауға мҥмкіндік беретін статистика бөлімі. Тәуелді айнымалының орта мәні мен предикторлардың орта мәндері арасындағы өзара байланыс регрессия теңдеуі тҥрінде өрнектеледі.

Регрессия теңдеуі - тәуелді айнымалы мен предикторлық айнымалылардың бастапқы статистикалық деректері негізінде таңдалынып алынатын математикалық функция. Көбінесе сызықты функция қолданылады. Бұл жағдайда регрессиялық талдау сызықты регрессиялық талдау деп аталады.

Регрессиялықталдаукорреляциялықталдауменөте тығызбайланысты. Корреляциялықталдаудасандықайнымалыларарасындағыбайланыстыңбағыты мен тығыздығы (күші) зерттеледі.

Регрессиялықталдаудасандықайнымалыларарасындағытәуелділіктің түрізерттеледі. Яғни, шынмәнісіндеекіәдіс те бірөзарабайланысты, бірақбіржақты, бір-бірінтолықтыраотырыпзерттейді. Практикадакорреляциялықталдаурегрессиялықталдаудыңалдында жүргізіледі. Корреляциялықталдауәдісіменбайланыстың бар екендігінанықтағаннанкейін бұл байланыстың түрінрегрессиялықталдауарқылыөрнектеугеболады.

Регрессиялықталдаудыңмақсаты- регрессия теңдеуіарқылытәуелдіайнымалының күтілетін орта мәніналдын - ала болжау.

Регрессиялықталдаудыңнегізгіміндеттері төмендегідей:

• 
  Тәуелділіктің түрі мен моделінанықтау;
  
• 
  Регрессия теңдеуінің (модельдің) параметрлерінбағалау;
  
• 
  Регрессия теңдеуініңмәнділігінтексеру;
  
• 
  Регрессия теңдеуініңкоэффициенттерініңмәнділігінтексеру;
  
• 
  Коэффициенттердіңаралықбағаларынтҧрғызу;
  
• 
  Модельдіңпопуляциядағыақиқат регрессия теңдеуіменсәйкестігінбағалау;
  
• 
  Тәуелдіайнымалының нүктелікжәнеаралықболжамдарын тұрғызу.
  

Корреляциялықталдаусияқтырегрессиялықталдау да айнымалыларарасындағысандықтәуелділіктібейнелейді. Регрессиялықталдаусебепті- салдарлытәуелділіктібейнелемейді. Айнымалылардыңсебеп-салдарлыбайланысы жөніндегіжорамалдарзерттеліпотырған құбылыстыңбиологиялықмазмұнынтеориялықталдаунегізіндеанықтауытиіс.

Регрессиялықталдаутүрлері:

Жайсызықты регрессия бірүздіксіз (сандық) предикторлықайнымалы мен оныменсызықтыбайланысқанбіртәуелдіайнымалыныңарасындағыбайланыстыбағалауүшінқолданылады.

Көптіксызықты регрессия екінемесеодан көп үздіксізнемесекатегориялықайнымалылар мен бірүздіксізтәуелдіайнымалыарасындағысызықтыбайланыстыбағалауүшінқолданылады.

Жайлогистикалық регрессия бірүздіксізнемесекатегориялықпредикторлықайнымалы мен біркатегориялық, әдеттебинарлытәуелдіайнымалы (мысалы, ауру- ауру емес) арасындағыбайланыстыбағалауүшінқолданылады.