Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 27 из 34

Способы построения индексов. Индексы в непрерывном времени.

Существует два подхода в интерпретации возможностей индексных показателей: обобщающий (синтетический) и аналитический, которые в свою очередь определяются разными задачами.

Суть обобщающего подхода - в трактовке индекса как показателя среднего изменения уровня исследуемого явления. В этом случае основной задачей, решаемой с помощью индексных показателей, будет характеристика общего изменения многофакторного экономического показателя.

Аналитический подход рассматривает индекс как показатель изменения уровня результативной величины, на которую оказывает влияние величина, изучаемая с помощью индекса. Отсюда и иная задача, которая решается с помощью индексных показателей: выделить влияние одного из факторов в изменении многофакторного показателя.

Способ построения агрегатных индексов заключается в том, что при помощи так называемых соизмерителей можно выразить итоговые величины сложной совокупности в отчетном и базисном периодах, а затем первую сопоставить со второй.

Анализ индексов в непрерывном времени можно назвать теоретическим. В этом случае динамика объемных и относительных величин задается непрерывными дифференцируемыми функциями y(t), x(t), a(t), и возможны три типа индексов: в момент времени t (моментные), сопоставляющие два момента времени t1 и t0 («момент к моменту») и два периода времени [t1, t1 + τ ] и [t0, t0 + τ ], τ |t1 − t0| («период к периоду»).

1) Моментные индексы.

Индивидуальными индексами такого типа являются моментные темпы роста, (нижние индексы-указатели объекта опущены):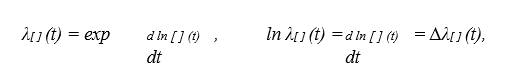



где λ[ ](t) — моментный темп роста,

∆λ[ ](t) — моментный темп прироста, а на месте [ ] стоит либо y — для объемной результирующей величины (стоимости), либо x — для объемной факторной величины (объема), либо a — для относительной величины (цены).
2) Индексы «момент к моменту» (индексы за период времени).

Индивидуальные индексы такого типа рассмотрены как непрерывные темпы роста за период (нижние индексы-указатели объектов опущены):



где λ[ ](t0, t1) — индекс за период [t0, t1], а на месте [ ], как и прежде, стоит либо y — для объемной результирующей величины (стоимости), либо x — для объемной факторной величины (объема), либо a — для относительной величины (цены).

3) Индексы «период к периоду».

Чаще всего предметом индексного анализа является динамика величин типа потока, поэтому именно непрерывные индексы «период к периоду» являются наиболее полным аналогом прикладных индексов, рассмотренных в пунктах 1–3 этого раздела.

Сначала необходимо определить следующие индивидуальные величины (здесь и далее нижний индекс-указатель объекта i опущен):

8. Стационарность, автоковариации и автокорреляции. Основные описательные статистики для временных рядов.

Временным рядом называют последовательность наблюдений, обычно упорядоченную во времени (хотя возможно упорядочение и по какому-либо другому параметру).

Стационарность или постоянство — свойство процесса не менять свои характеристики со временем.

Автокорреляция — статистическая взаимосвязь между последовательностями величин одного ряда, взятыми со сдвигом, например, для случайного процесса — со сдвигом по времени.

Автоковариацией с задержкой k (автоковариацией k -го порядка) стационарного процесса называется величина:



Автокорреляцией с задержкой k (автокорреляцией k -го порядка) стационарного процесса с ненулевой дисперсией называется величина: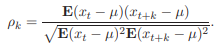



Aвтокорреляционной функцией (АКФ) называют последовательность автокорреляций {ρ_k}k=−∞,... ,+∞ .

Предположим, у нас имеется некоторые данные (временной ряд) x = x1,... ,x_T . Среднее и дисперсия временного ряда рассчитываются по обычным формулам:

и

Выборочная автоковариация k -го порядка вычисляется как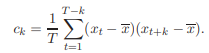



Статистической оценкой автокорреляции k-го порядка является выборочный коэффициент автокорреляции:



При анализе изменения величин ck и rk в зависимости от значения k обычно пользуются выборочными автоковариационной и автокорреляционной функциями, определяемыми как последовательности {c_k} и {r_k} соответственно.

Выборочная автокорреляционная функция играет особую роль в анализе стационарных временных рядов, поскольку может быть использована в качестве инструмента для распознавания типа процесса. При этом обычно анализируют график автокорреляционной функции, называемый коррелограммой.

Стационарным процессом называется такой случайный процесс, вероятностные свойства которого с течением времени не изменяются. Он протекает в приблизительно однородных условиях и имеет вид непрерывных случайных колебаний вокруг некоторого среднего значения.

Выборочная кросс-ковариация двух временных рядов, xt и yt , рассчитывается по формуле:



Она характеризует взаимосвязи двух рядов во времени, с различной величиной сдвига k . Следует помнить, что в отличие от автоковариации, кроссковариация не является симметричной по k , поэтому ее следует рассматривать и при положительных, и при отрицательных k .