Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 26 из 34

Метод инструментальных переменных.

Метод инструментальных переменных - метод оценки параметров регрессионных моделей, основанный на использовании дополнительных, не участвующих в модели, так называемых инструментальных переменных. Метод применяется в случае, когда факторы регрессионной модели не удовлетворяют условию экзогенности, то есть являются зависимыми со случайными ошибками. В этом случае, оценки метода наименьших квадратов являются смещенными и несостоятельными.

Метод инструментальных переменных основан на критике М. Фридменом оценивания кейнсианской функции потребления.

Общий вид функции потребления:

где Сit– объём потребления i-го домашнего хозяйства в t-ом году;

yit – объём доходов i-го домашнего хозяйства в t-ом году;

β – коэффициент предельной склонности к потреблению (0< β<1);

a – коэффициент автономного потребления;

εit – независимая случайная составляющая модели.

В соответствии с кейнсианской трактовкой модели потребления, коэффициент автономного потребления а равен нулю.

К основным недостаткам модели потребления можно отнести:

1) оценки неизвестных коэффициентов модели регрессии, рассчитанные традиционным методом наименьших квадратов, изменяются год от года;

2) в ходе экспериментов было доказано, что оценка коэффициента β для фермерских хозяйств ниже, чем для городского населения.

М. Фридмен показал невозможность применения традиционного метода наименьших квадратов для оценивания неизвестных коэффициентов модели регрессии (1) с помощью теории постоянных доходов.

Предположим, что справедливы следующие равенства:





Т – это индекс, означающий непостоянство (transitory) переменных.

П
усть переменные дохода yit и потребления Сit– этослучайные величины с нулевым математическим ожиданием и дисперсиями

соответственно, т. е. .

По Фридмену переменные дохода и потребления связаны отношением вида:


Задача состоит в определении значимости функции потребления (2) при значимости функции потребления (1).
Оценка неизвестного коэффициента β, полученная методом инструментальных переменных, выглядит следующим образом: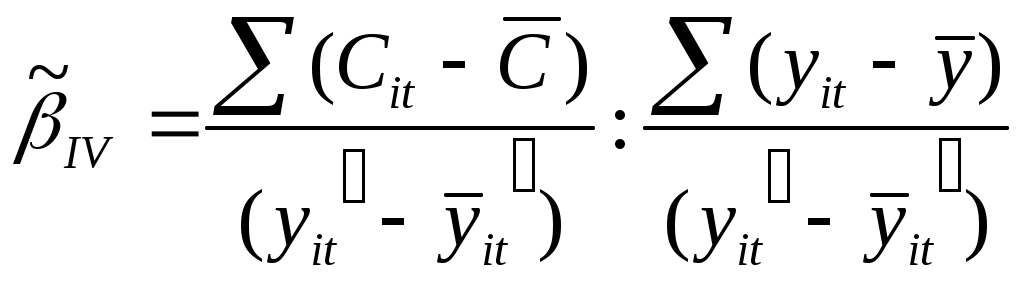





В общем случае инструментальная переменная z должна удовлетворять двум ϲʙᴏйствам:

1. 
   она должна тесно коррелировать с зависимой переменной у: cov(y,z)≠0;
   
2. 
   она не должна коррелировать со случайной ошибкой εt: cov(z,ε)=0.
   

Для модели множественной регрессии оценки неизвестных параметров модели рассчитываются по формуле:

8. Измерительная специфика экономических данных.

Как и для применений статистических методов в иных областях, в эконометрике решаются задачи описания данных, оценивания, проверки гипотез, прогнозирования, принятия статистических решений и др.

Однако в некоторых отношениях экономические данные отличаются от технических или астрономических, и эти отличия необходимо учитывать при выборе методов анализа конкретных экономических данных.

Многие экономические показатели неотрицательны. Значит, их надо описывать неотрицательными случайными величинами. А вот нормальные распределения принципиально не подходят, поскольку для них вероятность отрицательных значений всегда положительна.

Экономические процессы развиваются во времени, поэтому большое место в эконометрике занимают вопросы анализа и прогнозирования временных рядов, в том числе многомерных. При этом в одних задачах больше внимания уделяют изучению трендов (средних значений, математических ожиданий), например, при анализе динамики цен. В других же - важны отклонения от средней тенденции, например, при применении контрольных карт (карт Шухарта, кумулятивных сумм и др.). Однако в целом спектральный анализ и выделение различных периодов, циклов и типов волн менее распространены, чем, скажем, в биометрике и медицине.

Есть два принципиально различных подхода к изучению поведения организаций и людей. Согласно первому из них вполне допустимо описывать действия человека в вероятностных терминах, например, считать его ответ на заданный вопрос случайной величиной. Сторонники второго подхода полагают, что поведение человека или организации является детерминированным, определяется теми или иными причинами, а случайность при анализе выборки возникает лишь из-за случайности при отборе лиц для опроса или предприятий для изучения. Если ответ на вопрос имеет вид "да" - "нет", то число ответов "да" при первом подходе, как известно, имеет биномиальное распределение, а при втором - гипергеометрическое. К счастью для эконометриков, при увеличении объема генеральной совокупности эти два распределения сближаются (если доля выборки в генеральной совокупности мала, например, меньше 10%, то вместо гипергеометрического распределения можно использовать биномиальное), так что при обоих подходах можно применять одни и те же эконометрические методы, не тратя сил на решение философского вопроса о детерминированности или случайности поведения экономического агента- человека или организации.

Итак, специфика эконометрики проявляется не в перечне применяемых для анализа конкретных экономических данных статистических методов, а в частоте использования тех или иных методов.