Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 29 из 34

Стационарный временный ряд и его характеристики. Автокорреляционная функция стационарного временного ряда.

Статистический процесс называется строго стационарным, если взаимное распределение вероятностей m наблюдений инвариантно по отношению к общему сдвигу временного аргумента, т.е. совместная плотность распределения случайных величин xt1 , xt2 ,... ,xtm такая же, как для величин xt1+k, xt2+k,... ,xtm+k при любых целых значениях сдвига k .

Требование стационарности, определенное этими условиями, является до- статочно жестким. Говорят о слабой стационарности или стационарности второго порядка². В этом случае про-цесс имеет постоянное среднее значение µ = E(xt) для всех t, определяющее уровень, относительно которого он флуктуирует, постоянную дисперсию σ² = E(xt − µ)² для всех t и постоянную автоковариацию γk = E(xt − µ)(xt+k − µ) для всех t, т.е. ковариация между xt и xt+k зависит только от величины сдвига k и не зависит от t.

Мы можем называть временной ряд x1,... ,xT стационарным, если он может быть частью бесконечного стационарного процесса {xt}t=−∞,... ,+∞ . Свойства слабо стационарных процессов:

Автоковариацией с задержкой k (автоковариацией k -го порядка) ста- ционарного процесса называется величина: γk = E(xt − µ)(xt+k − µ). Автокорреляцией с задержкой k (автокорреляцией k -го порядка) ста- ционарного процесса с ненулевой дисперсией называется величина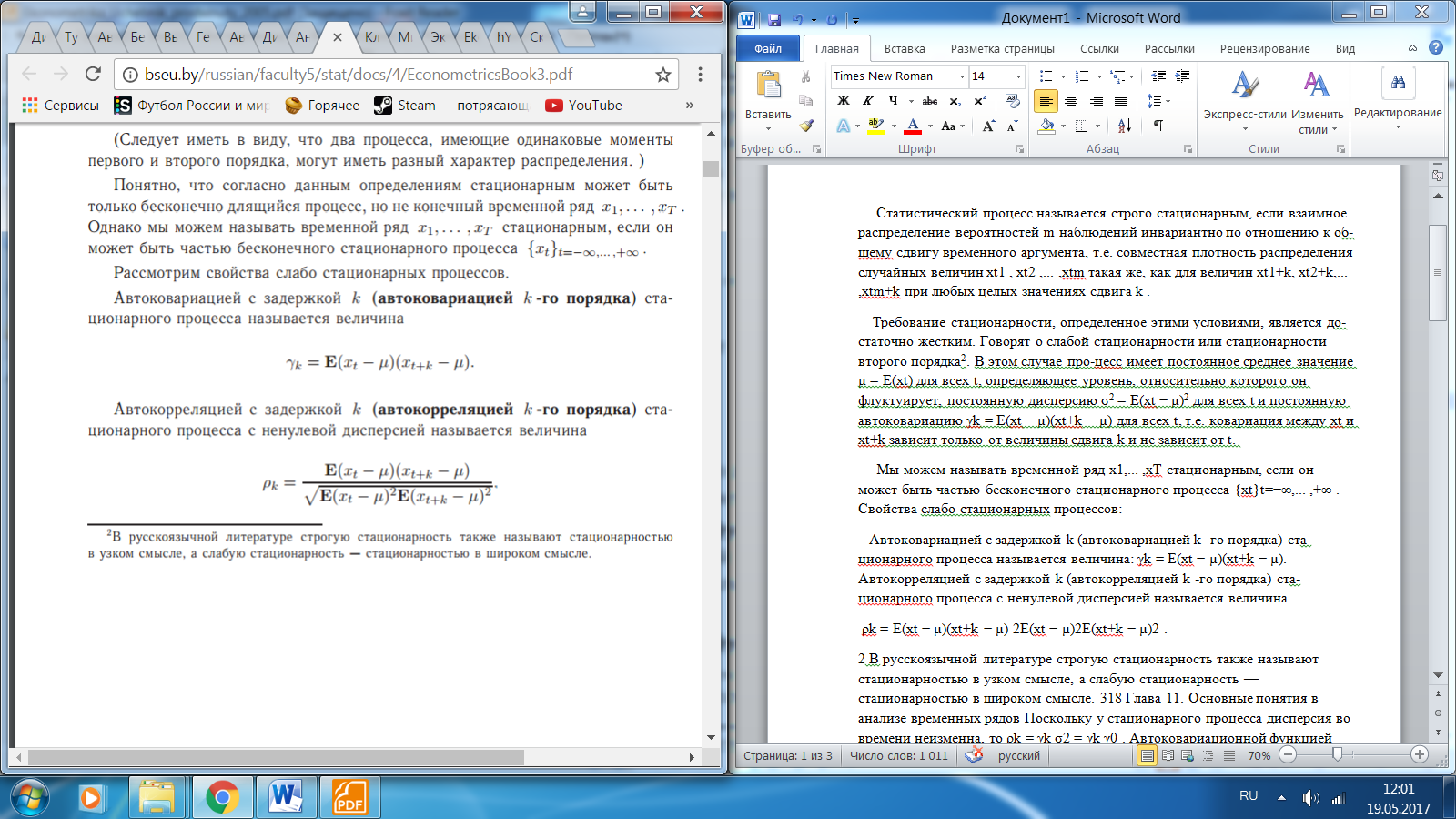



Поскольку у стационарного процесса дисперсия во времени неизменна, то ρk = γk /σ² = γk/ γ₀ .

Aвтокорреляционной функцией (АКФ) называют последовательность автокорреляций {ρk}k=−∞,... ,+∞ . Поскольку автокорреляционная функция симметрична, и ρ₀ известна ( ρ₀ = 1 ), то достаточно рассматривать k = 1,... , +∞

Среди стационарных процессов в теории временных рядов особую роль играют процессы типа «белый шум». Это неавтокоррелированные слабо ста- ционарные процессы с нулевым математическим ожиданием. Таким образом, процесс { εt } является «белым шумом», если µ = E(εt)=0, γ0 = E(ε² _t) = σ², γk = E(ε_t, ε_t−k)=0, ∀k = 0. Следовательно, для «белого шума» Γ_T = σ²I_T . Название «белый шум» связано с тем, что спектральная плотность такого процесса постоянна, то есть он содержит в одинаковом количестве все частоты, подобно тому как белый цвет содержит в себе все остальные цвета.

Для выявления наличия автокорреляции случайных величин ε_t может быть использован метод Бокса и Пирса (Box, Pierce), в соответствии с ко- торым статистика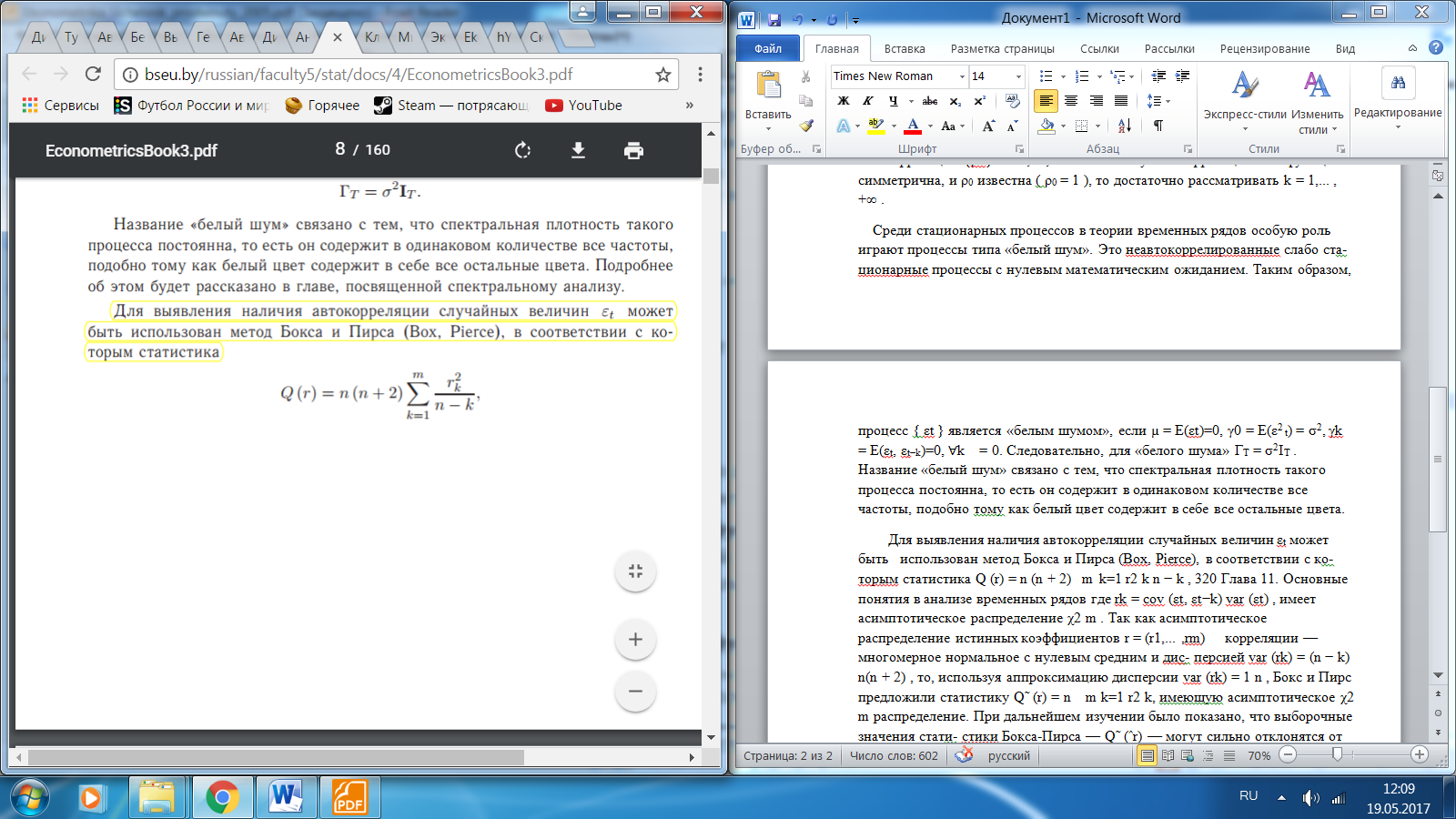

где r_k = cov (εt, εt−k)/ var (εt) , имеет асимптотическое распределение χ² m .

Бокс и Пирс предложили статистику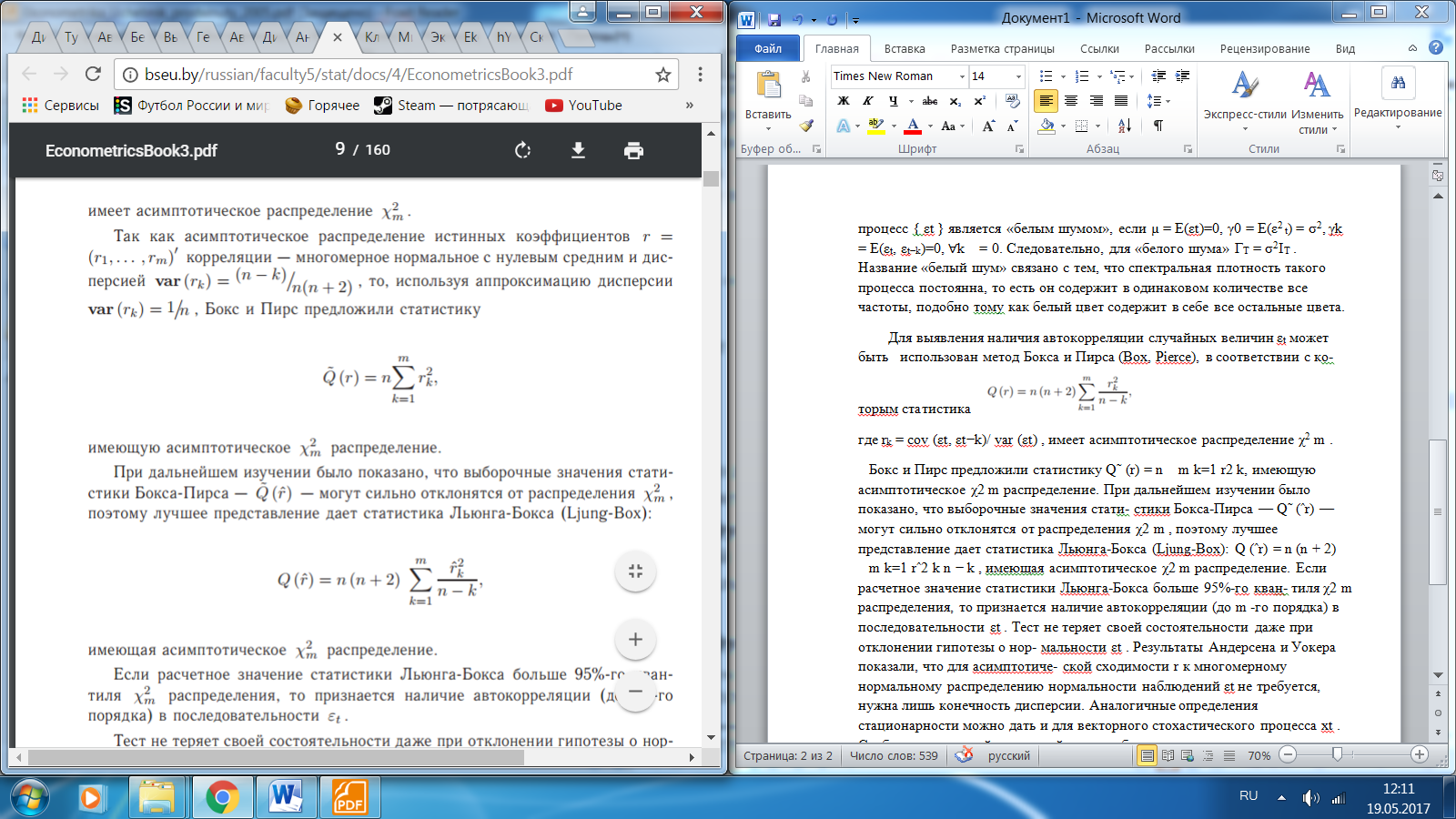

, имеющую асимптотическое χ2 m распределение.

Если расчетное значение статистики Льюнга-Бокса больше 95%-го кван- тиля χ2 m распределения, то признается наличие автокорреляции (до m -го порядка) в последовательности εt . Тест не теряет своей состоятельности даже при отклонении гипотезы о нор- мальности εt . Аналогичные определения стационарности можно дать и для векторного стохастического процесса xt . Слабо стационарный векторный процесс будет характеризоваться уже не скалярными автоковариациями γk и автокорреляциями ρk , а аналогичными по смыслу матрицами. Вне диагонали таких матриц стоят так называемые кросс-ковариации и кросс-корреляции.

8. Определение и свойства модели авторегрессии AR(p).

Моделью авторегрессии называется динамическая эконометрическая модель, в которой в качестве факторных переменных содержатся лаговые значения результативной переменной.

Пример модели авторегрессии:

yt=β0+β1xt+δ1yt–1+εt,

где β1 – это коэффициент, который характеризует краткосрочное изменение переменной у под влиянием изменения переменной х на единицу своего измерения;

δ1 – это коэффициент, который характеризует изменение переменной у в текущий момент времени t под влиянием своего изменения в предыдущий момент времени (t–1).

Промежуточным мультипликатором называется произведение коэффициентов модели авторегрессии (β1*δ1).

Промежуточный мультипликатор отражает общее абсолютное изменение результативной переменной у в момент времени (t+1).



Определение. Долгосрочным мультипликатором называется показатель, рассчитываемый как

Долгосрочный мультипликатор отражает общее абсолютное изменение результативной переменной у в долгосрочном периоде.

Если для модели авторегрессии выполняется условие |δ|<1, то при наличии бесконечного лага будет справедливым равенство:



В нормальной линейной модели регрессии все факторные переменные не зависят от случайной ошибки модели. Данное условие для моделей авторегрессии нарушается, потому что переменная yt-1 частично зависит от случайной ошибки модели εt. Следовательно, при оценке неизвестных коэффициентов традиционным методом наименьших квадратов ы получим смещённую оценку коэффициента при переменной yt–1.

При определении оценок неизвестных коэффициентов модели авторегрессии используется метод инструментальных переменных (IV – Instrumental variables).

Суть метода инструментальных переменных заключается в том, что переменная yt–1, для которой нарушается предпосылка применения метода наименьших квадратов, заменяется на новую переменную z, удовлетворяющую двум требованиям:

1) данная переменная должна тесно коррелировать с переменной yt–1: cov(yt–1,z)≠0;

2) данная переменная не должна коррелировать со случайной ошибкой модели εt: cov(z,ε)=0.

Предположим, что на основании собранных данных была построена модель авторегрессии вида:

yt=β0+β1xt+δ1yt–1+εt.

Рассчитаем оценки неизвестных коэффициентов данной модели с помощью метода инструментальных переменных.

В данной модели авторегрессии переменная yt коррелирует с переменной xt, следовательно, переменная yt–1 зависит от переменной xt–1. Охарактеризуем данную корреляционную зависимость с помощью парной модели регрессии вида:

yt–1=k0+k1xt–1+ut,

где k0 ,k1 – неизвестные коэффициенты модели регрессии;

ut – случайная ошибка модели регрессии.

Обозначим выражение k0+k1xt–1 через переменную zt–1. Тогда модель регрессии для переменной yt–1 примет вид:

yt–1= zt–1+ut.

Новая переменная zt–1  удовлетворяет свойствам, предъявляемым к инструментальным переменным:

1) она тесно коррелирует с переменной yt–1: cov(zt–1,yt–1)≠0;

2) она коррелирует со случайной ошибкой исходной модели авторегрессии εt:  cov(εt, zt–1).

Таким образом, исходная модель авторегрессии может быть представлена следующим образом:

yt=β0+β1xt+δ1(k0+k1xt–1+ut)+εt= β0+β1xt+δ1 zt–1+νt,

где νt= δ1 ut+ εt.

На следующем этапе оценки неизвестных коэффициентов преобразованной модели рассчитываются с помощью традиционного метода наименьших квадратов. Эти оценки будут являться оценками неизвестных коэффициентов исходной модели авторегрессии.