Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 32 из 34

Определение и свойства модели ARIMA.

ARIMA (англ.autoregressive integrated moving average) — интегрированная модель авторегрессии — скользящего среднего — модель и методология анализа временных рядов, иногда называемых моделями (или методологией) Бокса-Дженкинса. Являются расширением моделей ARMA для нестационарных временных рядов, которые можно сделать стационарными взятием разностей некоторого порядка от исходного временного ряда (так называемые интегрированные или разностно-стационарные временные ряды). Модель   означает, что разности временного ряда порядка   подчиняются модели ARMA(p, q). Эти модели используются при работе с временными рядами для более глубокого понимания данных или предсказания будущих точек ряда. Обычно модель упоминается, как ARIMA(p,d,q), где p,d и q — целые неотрицательные числа, характеризующие порядок для частей модели (соответственно авторегрессионной, интегрированной и скользящего среднего).

Методология ARIMA (Бокса-Дженкинса)

Подход ARIMA к временным рядам заключается в том, что в первую очередь оценивается стационарность ряда. Различными тестами выявляются наличие единичных корней и порядок интегрированности временного ряда (обычно ограничиваются первым или вторым порядком). Далее при необходимости (если порядок интегрированности больше нуля) ряд преобразуется взятием разности соответствующего порядка и уже для преобразованной модели строится некоторая ARMA-модель поскольку предполагается, что полученный процесс является стационарным, в отличие от исходного нестационарного процесса (разностно-стационарного или интегрированного процесса порядка d).

ARIMA применяется для прогнозирования объемов инвестирования в факторы производства, такие как производственный и человеческий капитал региональной экономик

Модели авторегрессии и скользящего среднего строятся исходя из условия стационарности. Стационарный процесс в сильном смысле — это процесс, в котором распределение случайной величины не изменяется со временем, а в слабом — это процесс с постоянным математическим ожиданием и дисперсией, в котором ковариация между значениями ряда зависит только от величины лага.

8. Построение и тестирование модели ARIMA на основе подхода Бокса – Дженкинса.

На первом шаге необходимо получить стационарный ряд. При тести­ровании исходных данных на стационарность прежде всего использует­ся визуальный анализ графика. Например, уже на этом этапе можно об­наружить ярко выраженную трендовую составляющую.

Также в методике Бокса—Дженкинса рекомендуется проводить ана­лиз АКФ (ЧАКФ). Быстрое убывание значений выборочной АКФ явля­ется простым критерием стационарности (аналогичное поведение долж­на демонстрировать и ЧАКФ).

Часто на этом этапе используются статистические тесты на нали­чие единичного корня (тест Дики—Фуллера, расширенный тест Дики- Фуллера).

Для перехода к стационарному ряду традиционно применяют опера­тор взятия последовательных разностей (процедуру дискретного диффе­ренцирования). Быстрое затухание АКФ будет свидетельствовать о том, что необходимая для стационарности ряда степень разности достигнута.

На втором шаге после получения стационарного ряда исследуется характер поведения выборочных АКФ и ЧАКФ, выдвигаются гипотезы о значениях параметров p(порядок авторегрессии) и q(порядок скользя­щего среднего).

При этом следует иметь в виду, что выборочные корреляционные функции могут не демонстрировать детального сходства с теоретическими. Поэтому для идентификации модели могут использоваться главные черты АКФ, при расхождении более тонких деталей, в результате формируется базовый набор, включающий 1—2 или даже большее число моделей.

На третьем шаге после осуществления идентификации моделей не­обходимо оценить их параметры. В современных эконометрических па­кетах прикладных программ используются разные подходы (МНК, нели­нейный МНК, метод максимального правдоподобия (ММП)). Все эти оценки при больших объемах выборок асимптотически эквивалентны.

На следующем, четвертом шаге для проверки каждой пробной моде­ли на адекватность анализируется ряд ее остатков. У адекватной модели остатки должны быть похожими на белый шум, т. е. их выборочные ав­токорреляции не должны существенно отличаться от нуля.

При проверке значимости коэффициентов АКФ используются два подхода:

• 
  проверка значимости каждого коэффициента автокорреляции отдельно;
  
• 
  проверка значимости множества коэффициентов автокорреля­ции как группы.
  

Первый подход опирается на работу Бартлетта, показавшего, что ес­ли модель адекватна исходным данным и ошибки представляют собой белый шум, то распределение коэффициентов автокорреляции прибли­жается к нормальному с нулевым математическим ожиданием и дисперсией  , т.е. к .

Поэтому если выборочный коэффициент автокорреляции  выходит за интервал , то нулевая гипотеза о равенстве нулю коэффициента р_к отвергается.

Второй подход опирается на Q-статистику Бокса—Пирса, позволяю­щую проверить равенство нулю сразу т первых значений АКФ остатков. Q-статистика определяется как

Q = n

При нулевой гипотезе об отсутствии автокорреляции статистика Q имеет -распределение сv= τ-p-q степенями свободы, где р,q - пара­метры ARMA модели.

Если Q> , то как группа первые τ коэффициентов автокорреля­ции значимы (т. е. не все , равны нулю).

В некоторых эконометрических пакетах включена модификация этого подхода — тест Бокса-Льюнга. Соответствующая статистика в этом случае определяется выражением:

= n(n+2)

имеет такое же асимптотическое распределение, как и Q, однако ее распределение ближе к для конечных выборок. В практических руководствах рекомендуется рассматривать (но не более 50).

Кроме того, при построении модели ARIMA необходимо проверить значимость коэффициентов (поt-критерию). При этом модель не должна содержать лишних параметров, т. е. уменьшение числа пара­метров будет способствовать появлению значимой автокорреляции ос­татков.

Если в результате проверки несколько моделей оказываются адек­ватными исходным данным, то при окончательном выборе следует учесть два требования:

■ повышение точности (качество подгонки модели);

■ уменьшение числа параметров модели.

Воедино эти требования сведены в информационном критерии Акайка (Akaikeinformationcriterion (AIC)), определяемом формулой: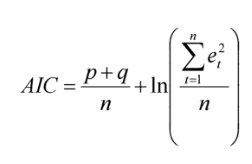



где  — уровни ряда остатков.

Очевидно, что выбор следует сделать в пользу модели с меньшим значением AIC.

Аналогичный характер носит критерий Шварца (Schwarzcriterion), усиливающий требование уменьшения количества параметров модели: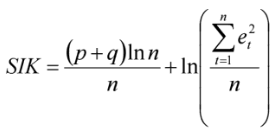



На заключительном этапе с помощью модели, выбранной на четвертом шаге, можно строить точечный и интервальный прогноз на L шагов вперед.