Вопросы к экзамену Полесский. 29. Тесты гетероскедастичнсоти. 46

• Название: 29. Тесты гетероскедастичнсоти. 46
• Анкор: Вопросы к экзамену Полесский
• Дата: 12.03.2023
• Размер: 5.25 Mb.
• Имя файла: Voprosy_k_ekzamenu_po_distsipline_Ekonometrika_1.doc
• Тип: Документы; #982220
• страница: 33 из 34

Прогнозирование на основе модели ARIMA.

Главная цель использования ARIMA моделей – построение прогноза за пределы выборки. Есть два источника неточности прогноза: первый – игнорирование будущих ошибок t  , второй – отклонение оценок коэффициентов модели от их истинных значений. Рассмотрим только первый источник ошибок прогноза или, другими словами, прогнозирование в рамках теоретических моделей. Рассмотрим проблему прогнозирования на примере ARMA1,1 и ARIMA1,1,0 моделей.

ARMA (1,1) модель. Прогнозирование

Из (2.11) получаем значение y в момент n 1:



Используя обозначение получаем:



Прогноз на один шаг, минимизирующий среднеквадратичное отклонение, равен информация, доступная в момент n . Из (2.14) получаем:



Ошибка прогноза и ее дисперсия равны



Используя две итерации уравнения (2.14), получаем



Отсюда аналогично (2.15) вычисляется прогноз на два шага: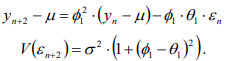



Продолжая итерации, можно получить



откуда видно, что прогноз стремится к среднему , когда горизонт прогноза возрастает. Можно показать, что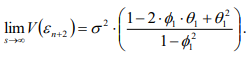



Заметим, что это выражение совпадает с дисперсией ряда y, полученной в (2.12.б).

ARIMA (1,1,0) модель. Прогнозирование

Прогноз нестационарного временного ряда несколько отличается от выше разобранного случая. Рассмотрим временной ряд t y первые разности которого t z являются AR1 процессом:





Многократное применение (2.16) дает:



Подставляя zt   из (2.16) в (2.17), получаем:



где,



Очевидно, что прогноз, минимизирующий среднеквадратичное отклонение, равен сумме первых трех слагаемых в (2.18). Заметим, что второе и третье слагаемые растут с ростом s. Ошибка прогноза на s шагов равна n s e. В силу формулы (2.19) дисперсия ошибки равна



Отсюда видно, что в случае нестационарного временного ряда диспепсия ошибки прогноза монотонно растет с ростом горизонта прогноза s.

8. Модели с биномиальной зависимой переменной. Линейная модель вероятности, логит- и пробит- модели. Оценивание моделей с биномиальной зависимой переменной.

Модели с биномиальной зависимой переменной.

Рассмотрим теперь модели, в которых зависимая переменная принимает только два значения, т.е. является фиктивной переменной. При этом придется отойти от модели линейной регрессии, о которой речь шла выше. Если изучается спрос на рынке некоторого товара длительного пользования, например, на рынке холодильников определенной марки, то спрос в целом возможно предсказывать с помощью стандартной регрессии. Однако, если изучать спрос на холодильники отдельной семьи, то изучаемая переменная должна быть либо дискретной (0 или 1), либо качественной (не покупать холодильник, купить холодильник марки A, купить холодильник марки B и т.д.). Аналогично, разные методы приходится применять при изучении рынка труда и при изучении решения

Линейная модель вероятности, логит и пробит

В биномиальную модель входит изучаемая переменная x, принимающая два значения, а также объясняющие переменные z, которые содержат факторы, определяющие выбор одного из значений. Без потери общности будем предполагать, что x принимает значения 0 и 1. Предположим, что мы оценили на основе имеющихся наблюдений линейную регрессию

x = zα + ε.

Очевидно, что для почти всех значений z построенная линейная регрессия будет предсказывать абсурдные значения изучаемой переменной x — дробные, отрицательные и большие единицы, что делает ее не очень полезной на практике. Более того, линейная модель не может быть вполне корректной с формальной точки зрения. Поскольку у биномиальной зависимой переменной распределение будет распределением Бернулли (биномиальным распределением с одним испытанием Бернулли), то оно полностью задается вероятностью получения единицы. В свою очередь, вероятность того, что x = 1, совпадает с математическим ожиданием x, если эта переменная принимает значения 0 и 1:

E(x) = Pr(x = 1) · 1 + Pr(x = 0) · 1 = Pr(x = 1).

С другой стороны, ожидание x при данной величине z для линейной модели равно

E(x) = zα + E(ε) = zα.

Отсюда следует, что обычная линейная регрессионная модель не совсем подходит для описания рассматриваемой ситуации, поскольку величина za, вообще говоря, не ограничена, в то время как вероятность всегда ограничена нулем и единицей. Ожидаемое значение зависимой переменной, E(x), может описываться только нелинейной функцией. Желательно каким-то образом модифицировать модель, чтобы она, с одной стороны, принимала во внимание тот факт, что вероятность не может выходить за пределы отрезка [0; 1], и, с другой стороны, была почти такой же простой как линейная регрессия. Этим требованиям удовлетворяет модель, для которой

Pr(x = 1) = F(zα),

где F(·) — некоторая достаточно простая функция, преобразующая zα в число от нуля до единицы. Естественно выбрать в качестве F(·) какую-либо дифференцируемую функцию распределения, определенную на всей действительной прямой. В дальнейшем мы рассмотрим несколько удобных функций распределения, которые удовлетворяют этим требованиям. Заметим, что если выбрать F(·), соответствующую равномерному распределению на отрезке [0; 1], то окажется, что



Таким образом, при zα ∈ [0; 1] получим «линейную регрессию». Это так называемая линейная модель вероятности. Однако, вообще говоря, такой выбор F(·) скорее не упрощает оценивание, а усложняет, поскольку в целом математическое ожидание зависимой переменной является здесь нелинейной функцией неизвестных параметров α (т.е. это нелинейная регрессия), причем эта функция недифференцируема. В то же время, если данные таковы, что можно быть уверенным, что величина zα далека от границ 0 и 1, то линейную модель вероятности можно использовать, оценивая ее как обычную линейную регрессию. То, что величина zα далека от границ 0 и 1, означает, что z плохо предсказывает x. Таким образом, линейная модель вероятности применима в случае, когда изучаемая зависимость слаба, и в имеющихся данных доля как нулей, так и единиц не слишком мала. Ее можно рассматривать как приближение для нелинейных моделей. Есть два удобных вида распределения, которые обычно используют для моделирования вероятности получения единицы в модели с биномиальной зависимой переменной. Оба распределения симметричны относительно нуля. 1) Логистическое распределение. Плотность логистического распределения равна



а функция распределения равна



Модель с биномиальной зависимой переменной с логистически распределенным отклонением называют логит. Для логита



2) Нормальное распределение (см. Приложение A.3.2). Модель с нормально распределенным отклонением ε называют пробит. При этом используется стандартное нормальное распределение, т.е. нормальное распределение с нулевым ожиданием и единичной дисперсией, N(0, 1). Для пробита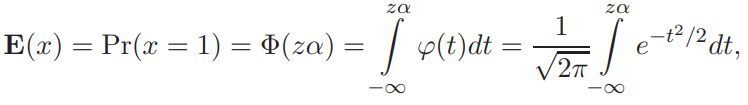



где Φ(·) — функция распределения стандартного нормального распределения, ϕ(·) — его плотность. Логистическое распределение похоже на нормальное с нулевым ожиданием и дисперсией π2/3 (дисперсия логистического распределения). В связи с этим оценки коэффициентов в моделях различаются примерно на множитель π/ √3 ≈ 1.8. Если вероятности далеки от границ 0 и 1 (около 0,5), то более точной оценкой множителя является величина ϕ(0)/λ(0) = Z8/π ≈ 1.6. При малом количестве наблюдений из-за схожести распределений сложно решить, когда следует применять логит, а когда — пробит. Различие наиболее сильно проявляется при вероятностях, близких к 0 и 1, поскольку логистическое распределение имеет более длинные хвосты, чем нормальное (оно характеризуется положительным коэффициентом эксцесса). Можно использовать в модели и другие распределения, например, асимметричные.

Оценивание моделей с биномиальной зависимой переменной

Требуется по N наблюдениям (xi, zi), i = 1, . . . , N, получить оценки коэффициентов α. Здесь наблюдения xi независимы и имеют биномиальное распределение с одним испытанием (т.е. распределение Бернулли) и вероятностью

Pr(xi = 1) = F(ziα).



Можно рассматривать модель с биномиальной зависимой переменной как модель регрессии:

xi = F(ziα) + ξi,

где ошибки ξi = xi − F(ziα) имеют нулевое математическое ожидание и независимы. Каждая из ошибок ξi может принимать только два значения, и поэтому их распределение мало похоже на нормальное. Кроме того, имеет место гетероскедастичность. Обозначим

pi = pi(α) = F(ziα).

В этих обозначениях дисперсия ошибки ξi равна

var(ξi) = E 6 (xi − pi) 2 7 = E(x2 i) − 2piE(xi) + p2 i = pi(1 − pi).

При выводе этой формулы мы воспользовались тем, что x2 i = xi и E(xi) = pi. Несмотря на эти нарушения стандартных предположений, данную модель, которая в общем случае представляет собой модель нелинейной регрессии, можно оценить нелинейным методом наименьших квадратов, минимизируя по α следующую сумму квадратов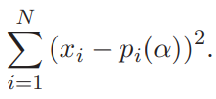



Для минимизации такой суммы квадратов требуется использовать какой-либо алгоритм нелинейной оптимизации. Этот метод дает состоятельные оценки коэффициентов α. Гетероскедастичность приводит к двум важным последствиям. Во-первых, оценки параметров будут неэффективными (не самыми точными). Во вторых, что более серьезно, ковариационная матрица коэффициентов, стандартные ошибки коэффициентов и t-статистики будут вычисляться некорректно (если использовать стандартные процедуры оценивания нелинейной регрессии и получения в ней оценки ковариационной матрицы оценок параметров). В частном случае модели линейной вероятности имеем линейную регрессию с гетероскедастичными ошибками: xi = ziα + ξi. Для такой модели можно предложить следующую процедуру, делающую поправку на гетероскедастичность: 1) Оцениваем модель обычным МНК и получаем оценки a. 2) Находим оценки вероятностей: pi = zia. 3) Используем взвешенную регрессию и получаем оценки a∗. Чтобы оценить взвешенную регрессию, следует разделить каждое наблюдение исходной модели на корень из оценки G и дисперсии ошибки, т.е. на величину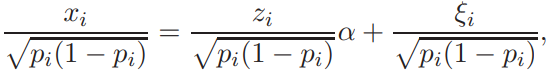





и далее применить к этой преобразованной регрессии обычный метод наименьших квадратов. При использовании данного метода получим асимптотически эффективные оценки a∗ и корректную ковариационную матрицу этих оценок, на основе которой можно рассчитать t -статистики. Те же идеи дают метод оценивания модели с произвольной гладкой функцией F(·). Для этого можно использовать линеаризацию в точке 0:

F(ziα) ≈ F(0) + f(0)ziα,

где f(·) — производная функции F(·) (плотность распределения). Тогда получим следующую приближенную модель:

xi ≈ F(0) + f(0) ziα + ξi,

или



Где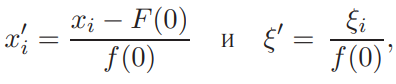



которую можно оценить с помощью только что описанной процедуры. Для симметричных относительно нуля распределений F(0) = 0, 5. В случае логита, учитывая λ(0) = 1\4, получаем



а в случае пробита, учитывая φ(0) = 1 "√2π , получаем



Таким образом, можно получить приближенные оценки для коэффициентов пробита и логита, используя в качестве зависимой переменной регрессии вместо переменной, принимающей значения 0 и 1, переменную, которая принимает значения ±2 для логита и ± для пробита



Ясно, что это хорошее приближение только когда величины ziα близки к нулю, то есть когда модель плохо описывает данные. Приближенные оценки можно получить также по группированным наблюдениям. Предположим, что все наблюдения разбиты на несколько непересекающихся подгрупп, в пределах каждой из которых значения факторов zi примерно одинаковы. Введем обозначения:



И



где Ij — множество наблюдений, принадлежащих j-й группе, Nj — количество наблюдений в j-й группе. Величина p¯j является оценкой вероятности получения единицы в случае, когда факторы принимают значение z¯j , т.е



Получаем модель регрессии, в которой в качестве зависимой переменной выступает F −1(¯pj ), а в качестве факторов — z¯j . В частном случае логистического распределения имеем: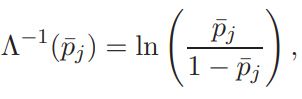



т.е. для логита зависимая переменная представляет собой логарифм так называемого «соотношения шансов». Чтобы такое приближение было хорошим, следует правильно сгруппировать наблюдения. При этом предъявляются два, вообще говоря, противоречивых требования:

– в пределах каждой группы значения факторов должны быть примерно одинаковы (идеальный случай

— когда в пределах групп zi совпадает, что вполне может случиться при анализе экспериментальных данных),

– в каждой группе должно быть достаточно много наблюдений. Описанный метод лучше всего подходит тогда, когда в модели имеется один объясняющий фактор (и константа), поскольку в этом случае проще группировать наблюдения.

В настоящее время в связи с развитием компьютерной техники для оценивания моделей с биномиальной зависимой переменной, как правило, используется метод максимального правдоподобия, рассмотрение которого выходит за рамки данной главы.