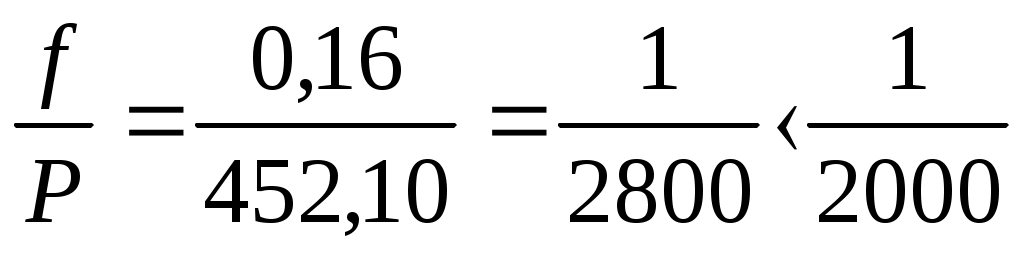4. Геодезические сети (1). 6. геодезические сети
 Скачать 0.81 Mb.
|
|
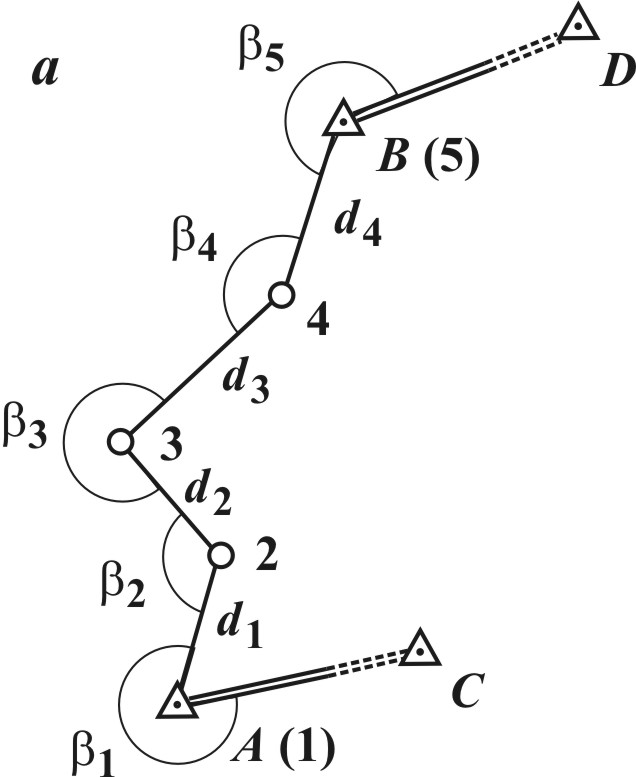
6. ГЕОДЕЗИЧЕСКИЕ СЕТИ Геодезической сетью называют совокупность пунктов на земной поверхности, закрепленных специальными центрами, положение которых определено в общей для них системе координат и высот. Различают плановые, высотные и пространственные сети. Плановые сети – это такие, в которых определены плановые координаты (плоские x, y или геодезические широта B и долгота L) пунктов. В высотных сетях определяют высоты пунктов относительно отсчетной поверхности, например, поверхности геоида (а точнее квазигеоида). В пространственных сетях определяют пространственные координаты пунктов, например, прямоугольные геоцентрические X, Y, Z или геодезические B, L, H. 6.1. Методы построения плановых сетей При построении плановых сетей отдельные пункты сети служат исходными – их координаты должны быть известны. Координаты остальных пунктов определяют с помощью измерений, связывающих их с исходными. Плановые геодезические сети создают следующими методами. Триангуляция – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют углы, а также длины некоторых сторон, называемых базисными сторонами (рис. 6.1). Положим, что в треугольнике АВP известны координаты пунктов А ( 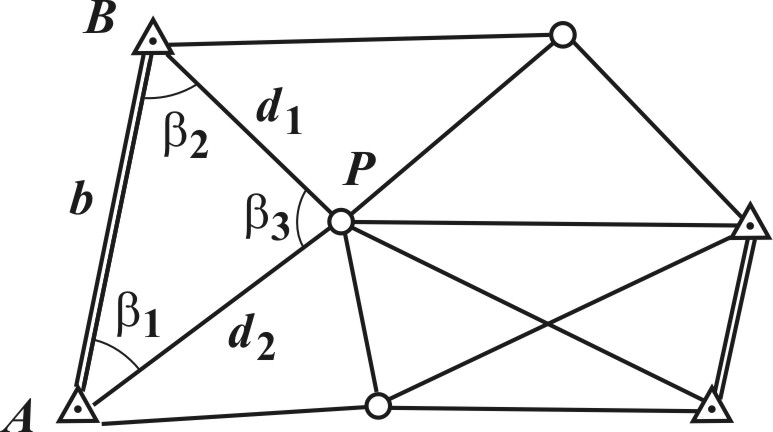 ,  ) и B ( ,  ). Это позволяет путем решения обратной геодезической задачи определить длину стороны  и дирекционный угол  направления с пункта A на пункт B. Длины двух других сторон треугольника АВP могут быть вычислены по теореме синусов ;  . Рис. 6.1. Схема сети триангуляции Продолжая подобным образом, вычисляют длины всех сторон сети. Если, кроме базиса b известны другие базисы (на рис. 6.1 базисы показаны двойной линией), то длины сторон сети можно вычислить с контролем. Дирекционные углы сторон АP и ВP треугольника АВP равны  ;  .Координаты пункта P определятся по формулам прямой геодезической задачи  ;  .Аналогично вычисляют координаты всех остальных пунктов. Трилатерация – метод определения планового положения геодезических пунктов путем построения на местности сети треугольников, в которых измеряют длины их сторон. Если в треугольнике АВP (рис. 6.1) известен базис b и измерены стороны  и  , то на основе теоремы косинусов, можно вычислить углы треугольника; ; ;  . (6.1)Так же вычисляют углы всех треугольников, а затем, как и в триангуляции, координаты всех пунктов. Линейно-угловая сеть строится, как правило, как сеть треугольников, в которых измеряют углы и длины сторон. Такие сети имеют большое число избыточных измерений и поэтому отличаются высокой надежностью. Полигонометрия – метод определения планового положения геодезических пунктов путем проложения ломаной линии (полигонометрического хода) или системы связанных между собой ломаных линий (сети полигонометрии), в которых измеряют углы поворота и длины сторон.
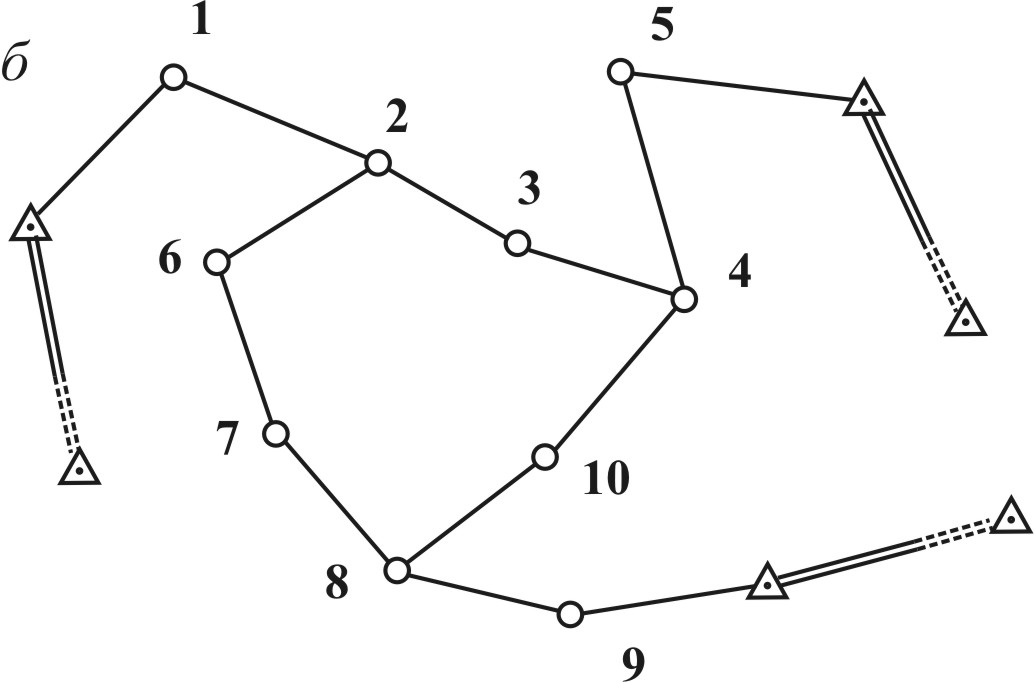
Рис. 6.2. Полигонометрия: а полигонометрический ход; б – система ходов Схема полигонометрического хода показана на рис. 6.2 a, где A и B – исходные пункты; CA и BD исходные направления, дирекционные углы которых известны; 1, 2, 3, 4, 5 точки (вершины) хода;  измеренные горизонтальные углы; измеренные длины сторон (i = 1, 2, …).На рис. 6.2 б показана схема системы полигонометрических ходов. Точки 2, 4, 8, где соединяются разные ходы, называются узловыми. Спутниковый метод определения координат геодезических пунктов основан на измерениях по сигналам спутников навигационных систем ГЛОНАСС (Россия) и GPS (США), выполняемых двумя (и более) наземными приемниками. По результатам измерений с высокой точностью определяют разности  ,  ,  геоцентрических координат между пунктами. Если координаты одного из пунктов известны, то, прибавив к ним измеренные разности, находят координаты остальных пунктов. Затем координаты преобразуют в геодезические или плоские прямоугольные.6.2. Основные виды плановых геодезических сетей Геодезические сети по назначению классифицируют на государственные геодезические сети, геодезические сети сгущения, геодезические сети специального назначения и съемочные сети. Государственная геодезическая сеть. Государственная геодезическая сеть покрывает всю территорию Российской Федерации и служит ее главной геодезической основой. Государственная геодезическая сеть (ГГС) предназначена для решения следующих основных задач, имеющих хозяйственное, научное и оборонное значение: установление и распространение единой системы координат на всю территорию страны и поддержание ее на уровне современных и перспективных требований; геодезическое обеспечение картографирования территории страны и акваторий окружающих ее морей; геодезическое обеспечение изучения земельных ресурсов и землепользования, кадастра, строительства, разведки и освоения природных ресурсов; обеспечение геодезическими данными средств наземной, морской и аэрокосмической навигации, аэрокосмического мониторинга природной и техногенной среды; изучение поверхности и гравитационного поля Земли и их изменений во времени; изучение геодинамических явлений; метрологическое обеспечение высокоточных технических средств определения местоположения и ориентирования. Положение пунктов ГГС определено сочетанием методов триангуляции, полигонометрии, астрономических и спутниковых измерений. Каталоги координат пунктов в системе СК-95 (координатная система 1995 года) хранятся в территориальных аэрогеодезических предприятиях Федерального Агентства «Роскартография». По мере совершенствования средств измерений и накопления новых данных ГГС модернизируется. Создаваемая в настоящее время сеть согласно “Основным положениям о государственной геодезической сети Российской Федерации” включает: фундаментальную астрономо-геодезическую сеть, высокоточную геодезическую сеть, спутниковую геодезическую сеть 1 класса, а также астрономо-геодезическую сеть и геодезические сети сгущения. Фундаментальная астрономо-геодезическая сеть (ФАГС) сеть пунктов, геоцентрические координаты которых определяются методами космической геодезии относительно центра масс Земли с погрешностью не более 10-15 см. Расстояния между пунктами 650 1000 км. Высокоточная геодезическая сеть (ВГС) обеспечивает распространение на всю территорию страны геоцентрической системы координат и уточнение параметров связи геоцентрической системы с действующей системой координат СК-95. Пункты ВГС определяются по наблюдениям спутников навигационных систем ГЛОНАСС и GPS. Расстояния между пунктами 150 300 км. Спутниковая геодезическая сеть 1 класса (СГС-1) сеть, создаваемая по мере необходимости по наблюдениям спутников систем ГЛОНАСС и GPS. Расстояния между пунктами 25 35 км. Характеристики точности рассмотренных выше сетей представлены в табл. 6.1, где D – расстояние между пунктами в км. Таблица 6.1
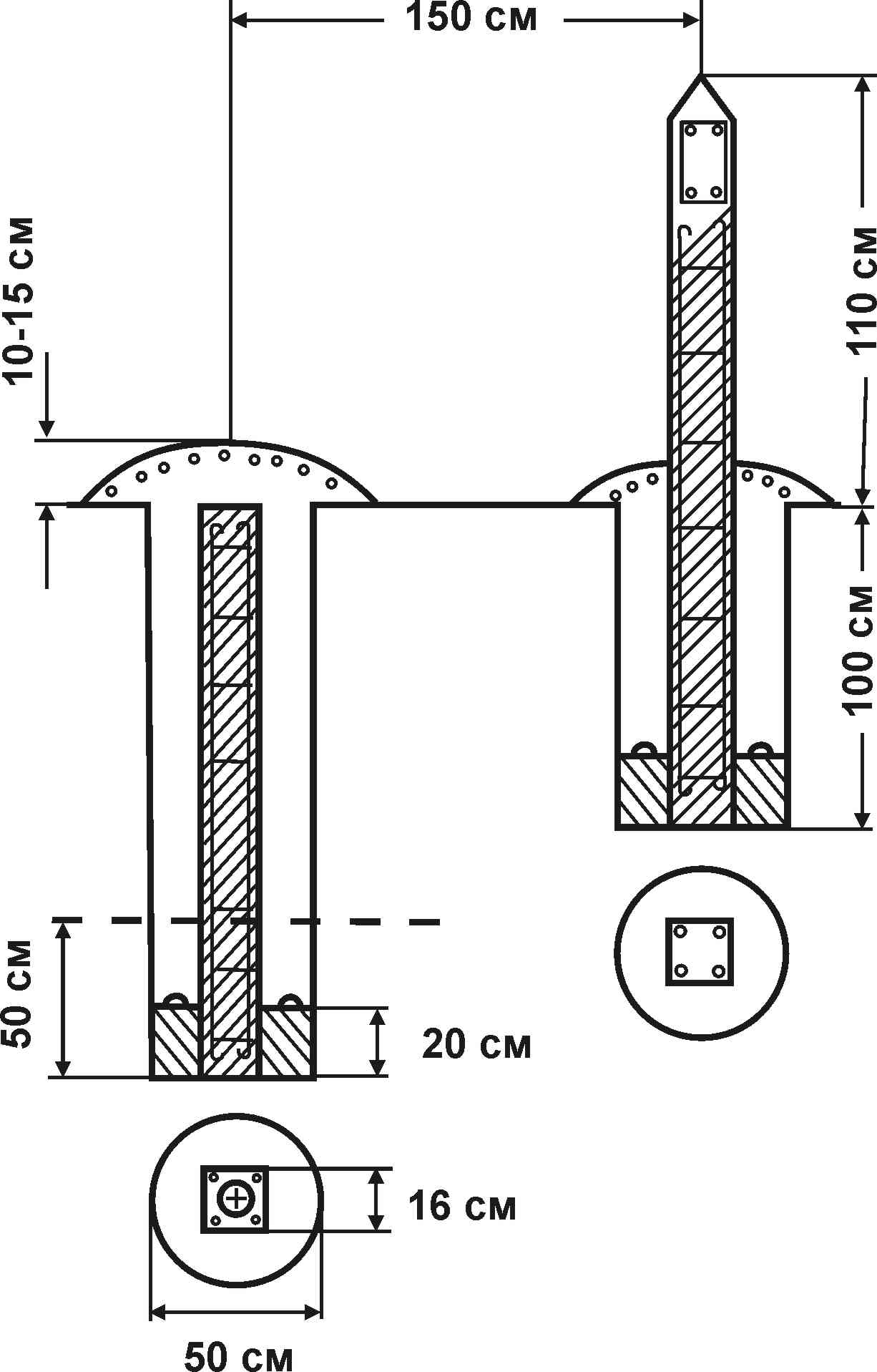
Астрономо-геодезическая сеть включает ранее созданные сети 1 и 2 классов. Сети 1 класса создавались в виде звеньев длиной 200 250 км, расположенных главным образом вдоль меридианов и параллелей и образующих замкнутые полигоны периметром 800 1000 км. Сеть 2 класса сплошная сеть внутри полигонов. Сети 3 и 4 классов опираются на пункты 1 и 2 классов и служат сгущению сети. Сети сгущения. Там, где требуется дальнейшее сгущение сети (например, в населенных пунктах), опираясь на государственную геодезическую сеть, развивают сети сгущения 1и 2 разряда, чем достигается плотность на 1  не менее 4 пунктов на застроенной территории и 1 пункт на незастроенной территории.Геодезические сети специального назначениясоздают в тех случаях, когда требуется особо высокая точность геодезической сети. Геодезическую сеть специального назначениястроят в государственной или в местной системе координат. Примерами таких сетей являются создаваемые на железных дорогах реперные системы, которые должны служить основой для всех съемочных и разбивочных геодезических работ, возникающих при проектировании, строительстве и текущем содержании железных дорог, а также для мониторинга пути и сооружений, межевания земель и кадастровой съемки в пределах полосы отвода. Съемочную сеть создают при выполнении съемки местности. Она развивается от пунктов государственной геодезической сети и сетей сгущения 1 и 2 разрядов. Но при съемке отдельных участков съемочная сеть может быть и самостоятельной, построенной в местной системе координат. В съемочных сетях, как правило, одновременно определяют положение пунктов в плане и по высоте. Предельные погрешности планового положения пунктов съемочной сети относительно исходных пунктов не должны превышать на открытой местности и на застроенной территории 0,2 мм в масштабе плана и 0,3 мм на местности, закрытой древесной и кустарниковой растительностью. Координаты пунктов съемочных сетей определяют проложением теодолитных ходов, построением триангуляции, засечками, спутниковым методом и др. Наиболее распространены теодолитные ходы. 6.3. Закрепление пунктов плановых геодезических сетей Пункты геодезических сетей закрепляют на местности специальными знаками центрами, призванными обеспечить устойчивость и длительную сохранность пунктов. Вид центра зависит от назначения сети и характера грунта. Официальными нормативными документами [16, 17, 21] установлены типовые конструкции центров, зависящие от класса пункта и местных условий. Они различны для районов сезонного промерзания грунтов, для районов многолетней мерзлоты, для районов распространения подвижных песков. На рис. 6.3 показан центр пункта государственной геодезической сети 1 - 4 классов для районов сезонного промерзания грунта. Центр представляет собой железобетонный пилон сечением  см и скрепленный с ним цементным раствором якорь диаметром 50 см и высотой 20 см. Основание центра располагают на 50 см ниже границы наибольшего промерзания грунта, но во всех случаях не менее 1,5 м от поверхности земли. На верху пилона крепится (цементным раствором или приваривается) чугунная марка, на верхней поверхности которой отмечена точка, к которой относятся координаты пункта.В 1,5 м устанавливают способствующий отысканию центра опознавательный знак – железобетонный столб с укрепленной на нем металлической охранной плитой, обращенной в сторону центра. До внедрения в геодезическое производство спутниковых технологий над центрами геодезических пунктов устанавливались наружные геодезические знаки деревянные или металлические сооружения, служащие объектом визирования на пункт и для подъема геодезических приборов над землей. Основными типами наружных знаков являлись пирамида и сигнал (рис. 6.4).
6.4. Создание съемочных сетей проложением теодолитных ходов Теодолитные ходы. Теодолитным ходом называют ход полигонометрии, выполненный методами, достаточными для обеспечения точности, требуемой в съемочных сетях. 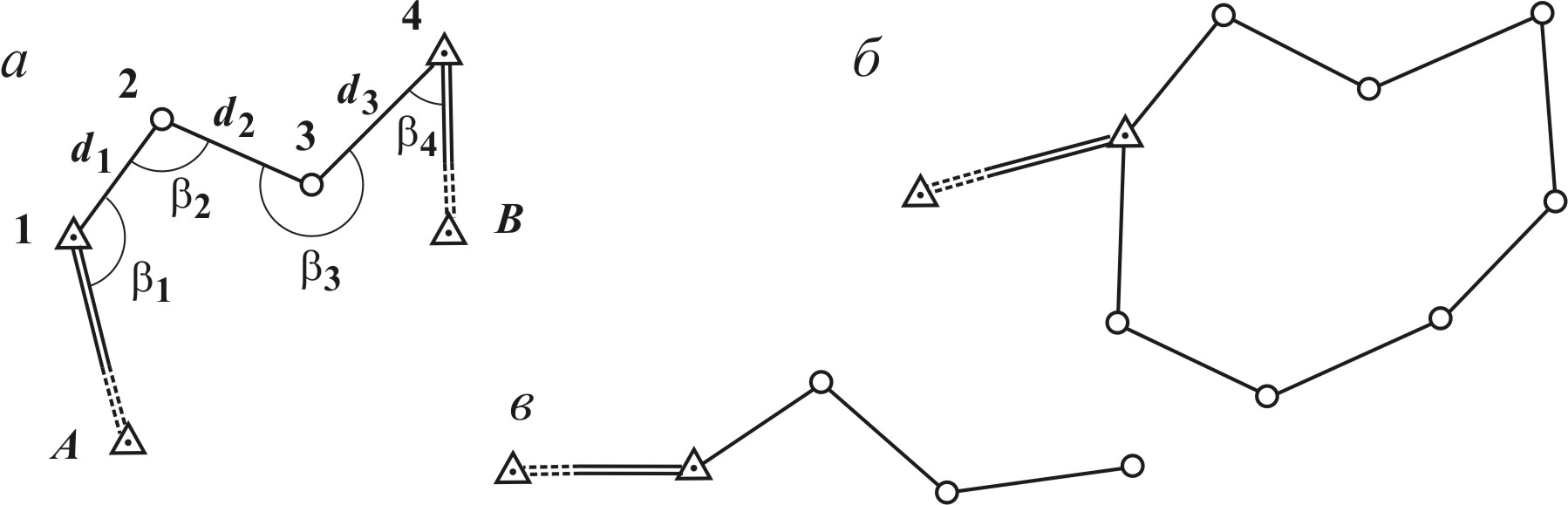 Рис. 6.5. Схемы теодолитных ходов: а – разомкнутого; б – замкнутого; в– висячего. По форме теодолитный ход может быть разомкнутым опирающимся на два исходных пункта и два исходных направления (рис. 6.5 а); замкнутым опирающимся на один исходный пункт и одно направление (рис. 6.5 б); висячим разомкнутым ходом, опирающимся на один исходный пункт и одно направление (рис. 6.5 в). Теодолитные ходы могут образовать систему теодолитных ходов с узловыми точками в местах их соединения (см. рис. 6.2 б). Проект съемочной сети составляют на топографической карте или плане. Но часто положение ходов выбирают непосредственно на местности в процессе рекогносцировки. При этом учитывают ограничения на длину хода между исходными пунктами, приведенные в табл. 6.2. Длины ходов, опирающихся на узловые точки, уменьшают на 30%. Таблица 6.2
Места для точек хода выбирают так, чтобы обеспечить взаимную видимость между ними, благоприятные условия для съемки окружающей местности, удобства установки геодезических приборов и сохранность точек. Точки ходов закрепляют деревянными кольями, костылями, металлическими трубами и т.п. Часть точек закрепляют знаками долговременной сохранности столбами, бетонными монолитами. Углы поворота теодолитного хода измеряют электронным тахеометром или теодолитом. При этом следят, чтобы на всех точках хода измерялись только правые, или только левые по ходу углы. Для измерения угла в его вершине устанавливают прибор, а в соседних точках – визирные цели. Угол измеряют одним приемом. Длины сторон измеряют электронным тахеометром или светодальномером, а при их отсутствии – землемерной лентой. Результаты измерения углов и расстояний записывают в журналы установленной формы. При выполнении измерений тахеометром запись результатов измерений выполняется автоматически в памяти прибора, откуда в последующем они вводятся для обработки в компьютер. Обработка разомкнутого теодолитного хода. Исходными данными в разомкнутом ходе (рис. 6.5 а) являются координаты начального и конечного пунктов 1 и 4 (  ,  ,  ,  ) и дирекционные углы начального A-1 и конечного 4-Bнаправлений ( и  ). При обработке вручную записи ведут в ведомость установленной формы (табл. 6.3). В графу 1 вписывают названия или номера точек. Вписывают исходные данные: в соответствующие строки графы 3 начальный и конечный дирекционные углы, а в графы 7 и 8 – координаты начального и конечного пунктов (исходные данные в таблице выделены жирным шрифтом). Вписывают результаты измерений: измеренные углы – в графу 2, горизонтальные проложения сторон хода – в графу 4. Уравнивание углов. Подсчитывают сумму измеренных углов  . Теоретически эта сумма должна быть равна: для правых углов  ;для левых углов  ,где n число измеренных углов. В табл. 6.3 углы правые. Отличие фактической суммы углов от теоретической представляет угловую невязку хода:  . (6.2)Таблица 6.3 Ведомость вычисления координат точек теодолитного хода
Вычисленную угловую невязку сравнивают с допустимой  .Если угловая невязка меньше допустимой, что указывает на доброкачественность угловых измерений и правильность вычислений, то невязку  распределяют поровну во все измеренные углы со знаком, противоположным знаку невязки. Полученные при этом поправки вписывают над измеренными углами в графу 2. Невязка редко делится на число углов без остатка. Поэтому поправки округляют, вводя большие в углы с более короткими сторонами. При этом сумма поправок должна равняться невязке с обратным знаком: = f. Вычисление дирекционных углов. Дирекционные углы вычисляют, используя начальный дирекционный угол и измеренные углы i, исправленные поправками , по формулам:для правых углов  ;для левых углов  . Здесь индексы i= 1, 2, …, n соответствуют номерам углов и сторон на рис. 6.5 а, причем 0 = нач и n = кон. Контролем правильности вычислений служит равенство вычисленного и заданного значений конечного дирекционного угла. Вычисление приращений координат выполняют по дирекционным углам и длинам сторон хода (графы 5 и 6).  ;  (i= 1, 2, …, n1). Вычислив суммы приращения абсцисс  и ординат  , находят координатные невязки ,  . (6.3) Вычисляют абсолютную невязку  и относительную невязку ходаfP,где  длина хода. Если относительная невязка не превосходит допустимой (обычно, 12000), то невязки fxи fy распределяют (см. записи курсивом в графах 5 и 6), в виде поправок к приращениям координат,пропорциональных длинам сторон, и со знаками, противоположными знакам невязок: ;  . (6.4)Суммы поправок должны равняться невязкам с обратным знаком:  ;  .Если из-за выполненных округлений равенства нарушаются, поправки, вычисленные по формулам (6.4), несколько изменяют, добиваясь соблюдения равенств. Вычисление координат точек теодолитного хода выполняют по формулам (см. графы 7 и 8)  ;  (i = 1, 2, …, n1). Контролем правильности вычислений служит совпадение вычисленных и заданных координат последней точки теодолитного хода. Обработка замкнутого теодолитного хода. Последовательность обработки замкнутого хода такая же как и разомкнутого. Но исходными в замкнутом теодолитном ходе служат координаты одного из пунктов хода и дирекционный угол одной из сторон. Это накладывает на обработку замкнутого хода следующие особенности. Угловая невязка вычисляется по формуле (6.2), в которой в отличие от разомкнутого хода  ,где n – число углов в полигоне. После распределения угловой невязки и вычисления дирекционных углов сторон хода контролируют правильность вычислений в конце должно быть получено то же значение дирекционного угла, которое было исходным. Невязки в координатах находят по формулам: ,  .Эти соотношения следуют из формул (6.3), где в данном случае  ,  . Распределив невязки fx и fy и вычислив координаты точек хода, контролируют правильность вычислений вычисленные в конце координаты начальной точки хода должны равняться исходным.6.5. Определение координат засечками Засечкой называется метод определения координат отдельной точки измерением элементов, связывающих ее положение с исходными пунктами. Для определения планового положения точки необходимо измерить два элемента. Для контроля, кроме необходимых, выполняют избыточные измерения. Засечки различают прямые, обратные и комбинированные. В прямой засечке измерения выполняют на исходных пунктах (рис. 6.6 a, г); в обратной – на определяемом пункте (рис. 6.6 б, д); в комбинированной – на исходных и определяемом пунктах (рис. 6.6 в). В зависимости от вида измерений засечки бывают угловые (рис. 6.6 a, б, в), линейные (рис. 6.6 г), линейно-угловые (рис. 6.6 д). Измеренные углы на рис. 6.6 отмечены дугами, измеренные расстояния – двумя штрихами. Рассмотрим вычисление координат в некоторых засечках. Прямая угловая засечка. На исходных пунктах A и B с координатами  ,  ,  , . (рис. 6.6 а) измеряют углы  и  . При обработке измерений сначала вычисляют дирекционные углы направлений AP и BP:  ;  .Дирекционные углы с координатами связаны формулами обратной геодезической задачи  ;  .Решая эти уравнения относительно xp и yp, получим формулы, по которым вычисляют координаты определяемой точки Р (формулы Гаусса):  ; (6.5) .Для контроля ординату yP вычисляют вторично по формуле: 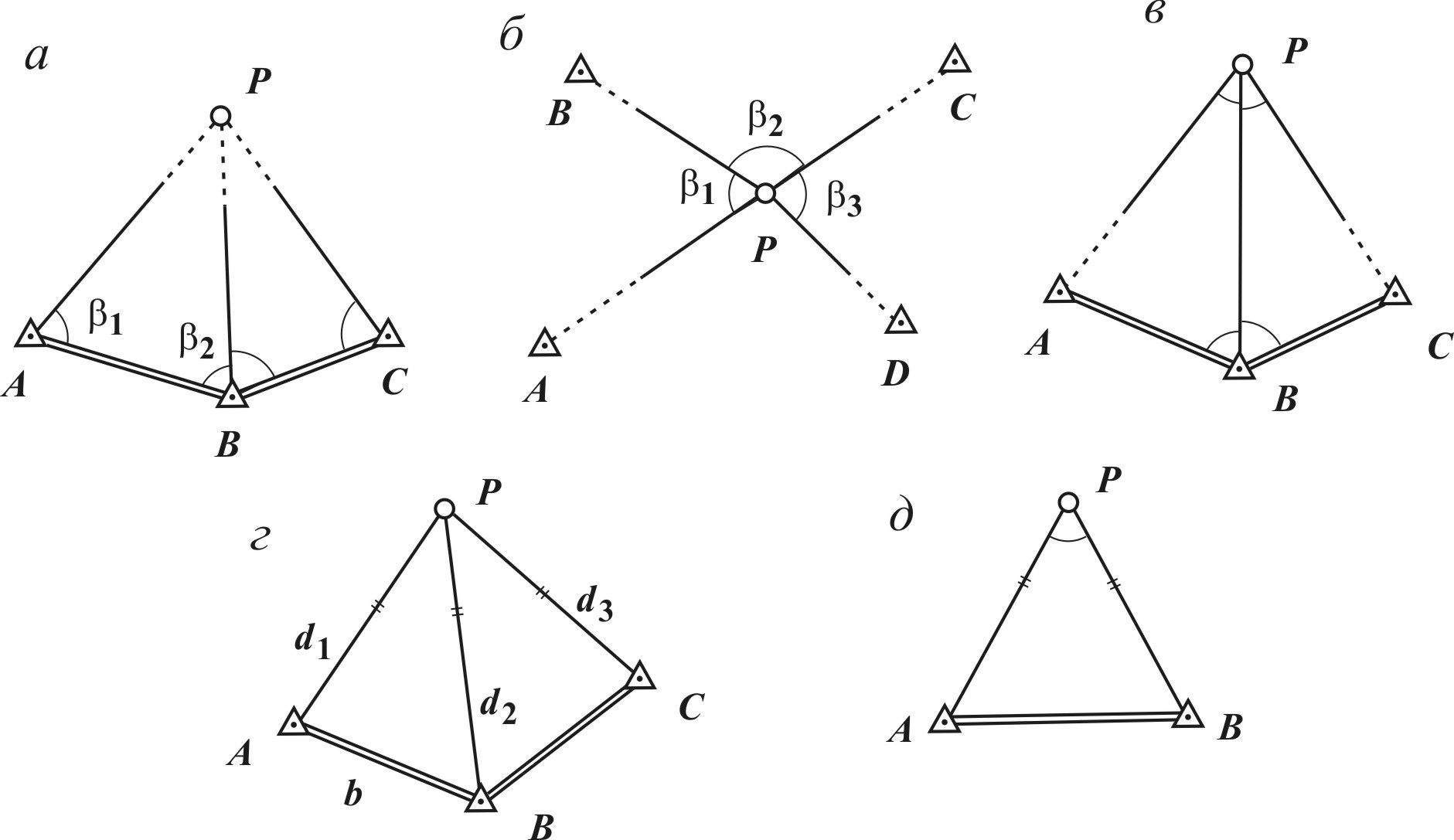 . Рис. 6.6. Схемы засечек: а – прямая угловая; б – обратная угловая; в – комбинированная угловая; г – линейная; д – линейно-угловая Если один из дирекционных углов  или  близок к  или  , то вместо формул (6.5 – 6.7) вычисления выполняют по формулам ; .Для контроля аналогичные измерения и вычисления выполняют, опираясь на другую исходную сторону BC. За окончательные значения координат определяемой точки принимают средние. Существуют и иные формулы решения прямой угловой засечки, например, формулы котангенсов углов треугольника (формулы Юнга):  ;  .Обратная угловая засечка. На определяемой точке P (рис. 6.6 б) измеряют углы и между направлениями на исходные пункты A, B и C. При этом исходные пункты выбирают такие, чтобы они с точкой P не оказались на одной окружности или вблизи нее. Координаты точки P вычисляют по формулам Гаусса (6.5 6.7), предварительно вычислив дирекционные углы: ;  .Для контроля измеряют избыточный угол  и вычисляют координаты, используя другую пару измеренных углов.Линейная засечка. Для определения координат точки Р (рис. 6.6 г) измеряют расстояния d1, d2. По формуле косинусов (6.1) находят углы треугольника АРВ. Вычисляют дирекционный угол АР = АВ A, а затем по формулам прямой геодезической задачи искомые координаты xP = xA + d1cosАР; yP = yA + d1sinАР. Для контроля измеряют избыточное расстояние d3 и вычисляют координаты из другого треугольника ВРС. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= 122,70; 
= 343,01;
4180 
м
= + 342,89 343,01 = 0,12 м
м
