пее. 7. варианты контрольных работ и методические указания по их выполнению
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
Тема 5. Модели стационарных и нестационарных временных рядов. Временным рядом (динамическим рядом) называется набор значений какого-либо показателя за несколько последовательных моментов или периодов времени. Отдельные наблюдения называются уровнями ряда. В общем виде при исследовании экономических процессов временного ряда выделяются несколько составляющих: yt = ut + vt + ct + εt (t=1, 2, …, n), где ut – тренд, vt – сезонная компонента, ct – циклическая компонента, εt – случайная компонента. Стационарные временные ряды. Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени. Временной ряд yt (t=1, 2, …,n) называется строго стационарным, если совместное распределение вероятностей n наблюдений y1, y2,…, yn такое же, как и nнаблюдений y1+τ, y2+τ,…, yn+τ при любых n, t, и τ. Таким образом, свойства строго стационарных рядов не зависят от момента времени t. Степень тесноты связи между последовательностями наблюдений временного ряда y1, y2, …, yn и y1+τ, y2+τ, …, yn+τ можно оценить с помощью выборочного коэффициента корреляции r(τ): 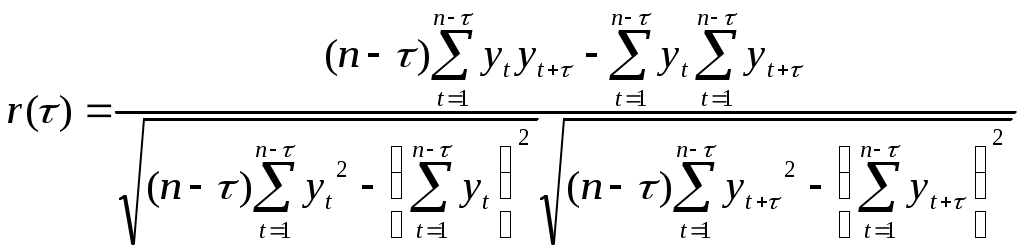 . .Так как он оценивает корреляцию между уровнями одного и того же ряда, его называют коэффициентом автокорреляции. Функция r(τ) называется выборочной автокорреляционной функцией, а ее график - коррелограммой. Кроме автокорреляционной функции при исследовании стационарных временных рядов рассматривают частную автокорреляционную функцию. Статистической оценкой частного коэффициента корреляции является выборочный частный коэффициент корреляции (или просто частный коэффициент корреляции): 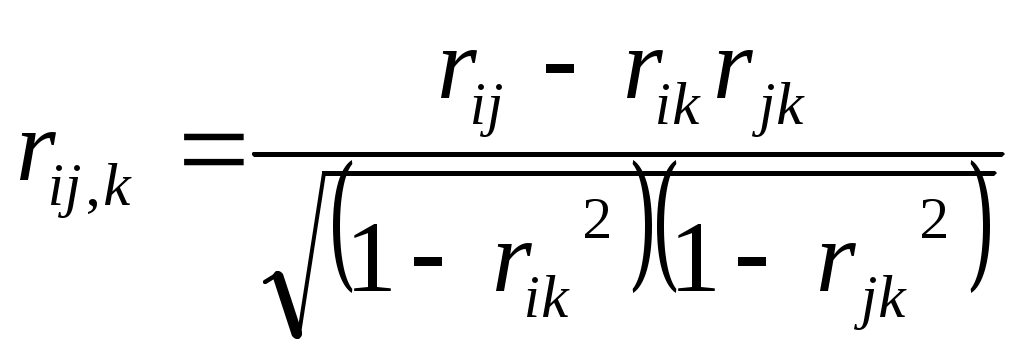 , ,где rij, rik rjk – выборочные коэффициенты корреляции. Так, выборочный частный коэффициент автокорреляции 1-го порядка между членами временного ряда yt и yt+2 при устранении влияния yt+1 определяется по формуле: где r(1), r(1,2), r(2) – выборочные коэффициенты автокорреляции между yt и yt+1, yt+1 и yt+2, и yt и yt+2 соответственно. Наиболее распространенным приемом устранения автокорреляции во временных рядах является подбор соответствующей модели: авторегрессионной АР(p), скользящей средней СС(q) или авторегрегрессионной модели скользящей средней АРСС(p,q) для остатков модели (в литературе можно встретить англоязычные названия моделей: авторегрессионной – АR(p), скользящей средней – MA(q) и авторегрегрессионной модели скользящей средней АRMA(p,q).) Идентификацией временного ряда называется построение для ряда остатков адекватной АРСС-модели, в которой остатки представляют собой белый шум, а все регрессоры значимы. Такое представление, как правило, не единственное, и один и тот же ряд может быть идентифицирован и с помощью АР-модели, и с помощью СС-модели. Авторегрессионная модель порядка p (модель АР(p)) имеет вид: yt = β0 + β1yt-1+ β2yt-2+…+ βpyt-p+εt, (t=1, 2, …,n), где β0, β1,… βp – некоторые константы. Если исследуемый процесс yt в момент t определяется его значениями только в преды-дущий период t-1, то получаем авторегрессионную модель 1-го порядка (или модель АР(1)). yt = β0 + β1yt-1 +εt, (t=1, 2, …,n), Наряду с авторегрессионными моделями временных рядов в эконометрике рассматриваются также модели скользящей средней. В них моделируемая величина задается линейной функцией от возмущений (остатков) в предыдущие моменты времени. Модель скользящей средней порядка q (модель СС(q)) имеет вид: yt = εt – γ1εt-1 – γ2εt-2 –…– γqεt-q (t=1, 2, …,n). Нередко используются и комбинированные модели временных рядов АР и СС, которые имеют вид: yt = β0 + β1yt-1+ β2yt-2+…+ βpyt-p+ εt – γ1εt-1 – γ2εt-2 –…– γqεt-q. Если все значения выборочной частной автокорреляционной функции порядка выше p незначимо отличаются от нуля, временной ряд следует идентифицировать с помощью модели, порядок авторегрессии которой не выше p. Если все значения выборочной автокорреляционной функции порядка выше q незначимо отличаются от нуля, временной ряд следует идентифицировать с помощью модели скользящей средней, порядок которой не выше q. Нестационарные временные ряды. Пусть имеется временной ряд yt = ρyt-1+ ξt. Предположим, что ошибки ξt независимы и одинаково распределены, т.е. образуют белый шум. Перейдем к разностным величинам: Δyt = λyt-1+ ξt, где Δyt = yt– yt-1, λ= ρ-1. Если ряд Δytявляется стационарным, то исходный нестационарный ряд ytназывается интегрируемым (или однородным). Нестационарный ряд ytназывается интегрируемым (однородным) k-го порядка, если после k-кратного перехода к приращениям dkyt = dk-1yt – dk-1yt-1, где d1yt = Δyt, получается стационарный ряд dkyt. Если при этом стационарный ряд dkyt корректно идентифицируется как АРСС(p,q), то нестационарный ряд ytобозначается как АРПСС(p,k,q). Это означает модель авторегрессии – проинтегрированной скользящей средней (другое обозначение - ARIMA(p,k,q)) порядков p, k, q, которая известна как модель Бокса-Дженкинса. Процедура подбора такой модели реализована во многих эконометрических пакетах. Модели с распределенными лагами. При исследовании экономических процессов приходится моделировать ситуации, когда значение результативного признака в текущий момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени. Величину l, характеризующую запаздывание в воздействии фактора на результат, называют лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, - лаговыми переменными. Модели, содержащие не только текущие, но и лаговые значения факторных переменных, называют моделями с распределенными лагами: В случае конечной величины максимального лага модель имеет вид: yt = a + b0xt + b1xt-1 + … + blxt-l +εt. Коэффициент b0 характеризует среднее абсолютное изменение yt при изменении xt на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора x. Этот коэффициент называется краткосрочным мультипликатором. Долгосрочный мультипликатор вычисляется по формуле: b = b0 + b1 + … + bl. Он показывает абсолютное изменение в долгосрочном периоде t+l результата y под влиянием изменения на 1 ед. фактора x. Величины βj=bj/b (j = 0,…,l) называются относительными коэффициентами модели с распределенным лагом. Средний лаг определяется по формуле средней арифметической взвешенной: и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора. Высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени. Медианный лаг (lMe) – представляет собой период времени, в течение которого буде реализована половина общего воздействия фактора на результат и определяется следующим соотношением: Оценка модели с распределенными лагами зависит от того, конечное или бесконечное число лагов она содержит. Метод Алмон. Предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному закону распределения: bj = c0 + c1·j + c2·j2 + … + ck·jk. (5.1) Уравнение регрессии примет вид: yt = a +c0·z0 + c1·z1 + c2·z2 + … + ck·zk + εt, (5.2) где Схема расчета параметров модели: устанавливается максимальная величина лага l; определяется степень полинома k, описывающего структуру лага; по соотношениям (5.3) рассчитываются значения переменных z0, z1,…, zk; обычным методом наименьших квадратов определяются параметры уравнения линейной регрессии yt от zi(5.2); рассчитываются параметры исходной модели по формулам (5.1). Метод Койка. Предполагается, что коэффициенты при лаговых значениях переменной убывают в геометрической прогрессии: Уравнение регрессии преобразуется к виду: yt = a + b0xt + b0·λ xt-1 + b0·λ2 xt-2 +… +εt. После ряда преобразований получается уравнение авторегрессии первого порядка: yt = a·(1 – λ) + b0·xt + (1 – λ) yt-1 + ut, где ut = εt – λ εt-1. Определив параметры данной модели, находятся λ и оценки параметров a и b0 исходной модели. Далее из соотношения (5.4) определяются параметры модели b1, b2,… . Величина среднего лага в модели Койка определяется формулой: Пример 5. По данным о динамике товарооборота (Y, млрд. руб.) и доходах населения (X, млрд. руб.) была получена следующая модель с распределенными лагами: Yt = 0,50∙Xt + 0,25∙Xt-1+ 0,13∙Xt-2 + 0,13∙Xt-3 + εt. (0,06) (0,04) (0,04) (0,06) В скобках указаны значения стандартных ошибок для коэффициентов регрессии. Значение R2 = 0,98. Задание: Проанализируйте полученные результаты регрессионного анализа. Дайте интерпретацию параметров модели: определить краткосрочный и долгосрочный мультипликаторы. Определите величину среднего лага и медианного лага. Решение. 1. Проверка значимости отдельных коэффициентов модели дает следующие расчетные значения t-статистики для коэффициентов: tb0 = 0,50/0,06 = 8,33; tb1 = 0,25/0,04 = 6,25; tb2 = 0,13/0,04 = 3,25; tb3 = 0,13/0,06 = 2,17. Таким образом, все коэффициенты оказываются значимыми, и выбор величины лага l=3 является оправданным. Об адекватности полученной модели свидетельствует и высокое значение коэффициента детерминации. 2. Краткосрочный мультипликатор в модели равен b0 = 0,50. Он показывает, что увеличение доходов на 1 млрд. руб. ведет в среднем к росту товарооборота на 0,5 млрд. руб. в том же периоде. Долгосрочный мультипликатор для полученной модели составит: b = b0 +b1 +b2 +b3 = 0,50 + 0,25 + 0,13 + 0,13 = 1,01. Получаем, что увеличение доходов на 1 млрд. руб. в настоящий момент времени в долгосрочной перспективе (через 3 месяца) приведет к росту товарооборота на 1,01 млрд. руб. Рассчитаем относительные коэффициенты модели: β0 = 0,50/1,01 = 0,495; β1 = 0,25/1,01 = 0,248; β2 = 0,13/1,01 = 0,129; β3 = 0,13/1,01 = 0,129. Следовательно, 49,5% общего увеличения товарооборота, вызванного ростом доходов населения, происходит в текущий момент времени; 24,8% - в момент времени (t+1); 12,9% - в моменты времени (t+2) и (t+3). 3. Средний лаг в модели определяется следующим образом: Величина среднего лага меньше месяца, что подтверждает, что эффект роста доходов населения на объем товарооборота проявляется сразу же. Медианный лаг для данной модели составляет чуть более 1 месяца. Тема 6. Прогнозирование, основанное на использовании моделей временных рядов. Характерной чертой адаптивных методов прогнозирования является их способность непрерывно учитывать эволюцию динамических характеристик изучаемых процессов, «адаптироваться» к этой эволюции, придавая тем больший вес, тем более высокую информационную ценность имеющимся наблюдениям, чем ближе они к текущему моменту прогнозирования. В основе процедуры адаптации лежит метод проб и ошибок. По модели делается прогноз на один интервал по времени. Через один шаг моделирования анализируется результат: насколько он далек от фактического значения. Затем в соответствии с моделью происходит корректировка. После этого процесс повторяется. Таким образом, адаптация осуществляется рекуррентно с получением каждой новой фактической точки ряда. Методы экспоненциального сглаживания. Модель Брауна. Пусть анализируемый временной ряд x(t) представлен в виде: x(t) = a0 + ε(t), где a0– неизвестный параметр, не зависящий от времени, ε(t) - случайный остаток со средним значением, равным нулю, и конечной дисперсией. В соответствии с методом Брауна прогноз x*(t+τ) для неизвестного значения x(t+τ) по известной до момента времени t траектории ряда x(t) строится по формуле: x*(t; τ) = S(t), где значение экспоненциально взвешенной скользящей средней S(t) определяется по рекуррентной формуле: S(t)= αx(t) + (1-α)S(t-1). Коэффициент сглаживания α можно интерпретировать как коэффициент дисконтирования, характеризующий меру обесценивания информации за единицу времени. Из формулы следует, что экспоненциально взвешенная скользящая средняя является взвешенной суммой всех уровней ряда x(t), причем веса уменьшаются экспоненциально по мере удаления в прошлое. В качестве S(0) берется, как правило, среднее значение ряда динамики или среднее значение нескольких начальных уровней ряда. Случай линейного тренда: x(t) = a0 + a1t + ε(t). В этом случае прогноз x*(t; τ) будущего значения определяется соотношением: x*(t; τ) = а пересчет коэффициентов Начальные значения коэффициентов берутся из оценки тренда линейной функцией. Модель Хольта. В модели Хольта введено два параметра сглаживания α1 и α 2 (0< α 1, α 2 <1). Прогноз x*(t;l) на l шагов по времени определяется формулой: x*(t; τ) = а пересчет коэффициентов Модель Хольта-Уинтерса. Эта модель помимо линейного тренда учитывает и сезонную составляющую. Прогноз x*(t;τ) на τ шагов по времени определяется формулой: x*(t;τ) = где f(t) – коэффициент сезонности, а T – число временных тактов (фаз), содержащихся в полном сезонном цикле. Видно, что в данной модели сезонность представлена мультипликативно. Формулы обновления коэффициентов имеют вид:  Модель Тейла-Вейджа. Если исследуемый временной ряд имеет экспоненциальную тенденцию с мульти-пликативной сезонностью, то после логарифмирования обеих частей уравнения получается модель с линейной тенденцией и аддитивной сезонностью или модель Тейла-Вейджа. Имеется модель: x(t) = a0(t) + g(t) + δ(t), a0(t) = a0(t-1) + a1(t). Здесь a0(t) – уровень процесса после устранения сезонных колебаний, a1(t) – аддитивный коэффициент роста, ω(t) – аддитивный коэффициент сезонности и δ(t) – белый шум. Прогноз x*(t;τ) на τ шагов по времени определяется формулой: x*(t;τ) = Коэффициенты вычисляются рекуррентным способом по формулам:  Для определения оптимальных значений параметров адаптации перебирают различные наборы их значений и сравнивают получающиеся при этом среднеквадратические ошибки прогнозов. Тема 7. Системы линейных одновременных уравнений. Нередко при моделировании реальных экономических объектов для объяснения механизма их функционирования приходится строить систему уравнений, состоящую из тождеств и регрессионных уравнений. Система уравнений в эконометрических исследованиях может быть построена по-разному. Возможна система независимых уравнений, когда каждая зависимая переменная (y) рассматривается как функция одного и того же набора объясняющих факторов (x1, х2,…,хm): 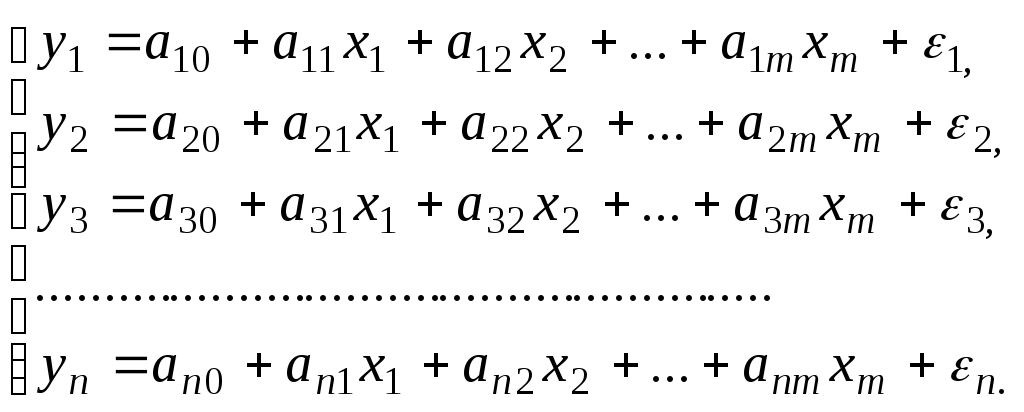 Каждое уравнение такой системы может рассматриваться самостоятельно, а для нахождения его параметров применяется метод наименьших квадратов. Если зависимая переменная y одного уравнения выступает в виде фактора x в другом уравнении, то можно построить модель в виде системы рекурсивных уравнений:  Каждое уравнение такой системы также может рассматриваться самостоятельно, а его параметры оцениваются методом наименьших квадратов. В системе линейных одновременных уравнений одни и те же переменные (y) одновременно рассматриваются как зависимые в одних уравнениях и независимые в других. Такая система уравнений называется структурной формой модели. Каждое уравнение в системе одновременных уравнений не может рассматриваться самостоятельно, поэтому метод наименьших квадратов для оценки параметров неприменим. В общем случае структурная форма модели имеет вид:  Зависимые переменные, число которых равно числу уравнений в системе, называются эндогенными переменными и обозначаются y. Предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них, называются экзогенными переменными и обозначаются x. Примером системы одновременных уравнений является модель спроса и предложения, когда объем спроса на товар (Qd) определяется его ценой (P) и доходом потребителя (I), объем предложения (Qs) – его ценой (P) и достигается равновесие между спросом и предложением: 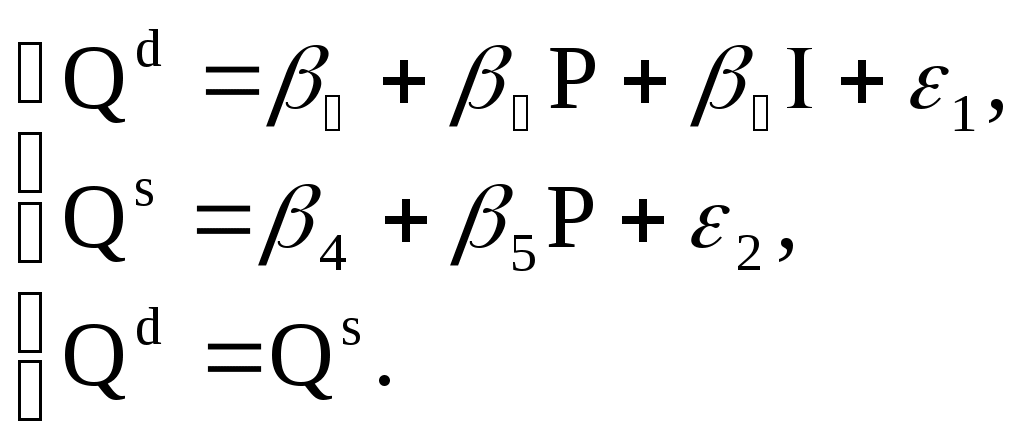 Переменные Qd, Qs, и P формируют свои значения внутри модели, согласно уравнениям системы, и таким образом, являются эндогенными переменными. Переменная I полагается заданной, ее значения формируются вне модели, и она является экзогенной. Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Поэтому для определения структурных коэффициентов модель преобразуется в приведенную форму модели. Приведенная форма модели представляет систему линейных функций эндогенных переменных от экзогенных:  где δij – коэффициенты приведенной формы модели. При переходе от приведенной формы модели к структурной приходится сталкиваться с проблемой идентифицируемости модели. Идентифицируемость – это единственность соответствия между приведенной и структурной формами модели. С позиции идентифицируемости структурные модели можно подразделить на три вида: идентифицируемые; неидентифицируемые; сверхидентифицируемые. Модель идентифицируема, если все ее структурные коэффициенты определяются однозначно, единственным образом, по коэффициентам приведенной формы модели, т.е. число параметров структурной модели равно числу параметров приведенной формы модели. Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два и более значений одного структурного коэффициента. Необходимое условие идентифицируемости: D + 1 = H – уравнение идентифицируемо; D + 1 < H – уравнение неидентифицируемо; D + 1 > H – уравнение сверхидентифицируемо, где H – число эндогенных переменных в уравнении, D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Достаточное условие идентифицируемости: Уравнение идентифицируемо, если по отсутствующим в нем переменным можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без единицы. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений неидентифицируемо, то и вся модель считается неидентифицируемой. Рассмотрим ряд модификаций модели спроса-предложения. 1. Модель спроса-предложения с учетом тренда. Если предположить изменение спроса со временем, то в первое уравнение системы необходимо добавить временной тренд:  Приведенная форма модели запишется в виде: Исходная система не оказывается идентифицируемой, поскольку параметр β5 является сверхидентифицируемым. Чтобы это показать, запишем систему в следующем виде:  Сравнивая две записи приведенной формы, легко заметить, что оценку β5. можно получить двумя способами: как e/b и f/c. 2. Модель спроса-предложения с учетом налога. Предположим, что продавцы товаров облагаются специальным налогом T. Величина налога меняется со временем и представлена временным рядом. Тогда система уравнений запишется следующим образом: 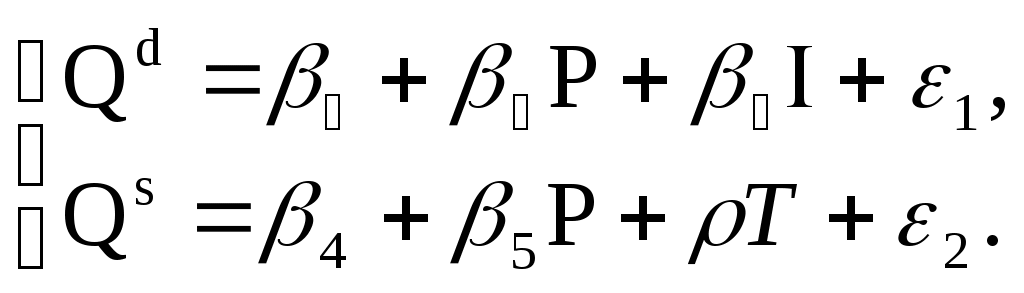 В данном случае система является идентифицируемой, но если теперь предположить, что доход I на протяжении длительного времени является постоянной величиной, то в уравнении спроса переменную I следует исключить.  Данная система уравнений уже не является идентифицируемой. Получить идентифицируемое уравнение формирования предложения можно, наложив ограничение на структурные коэффициенты: β5 = -ρ. Смысл этого ограничения в том, что мы полагаем, что продавцы исходят из суммы, которую они получают после уплаты налога, т.е. Р* = Р - Т. 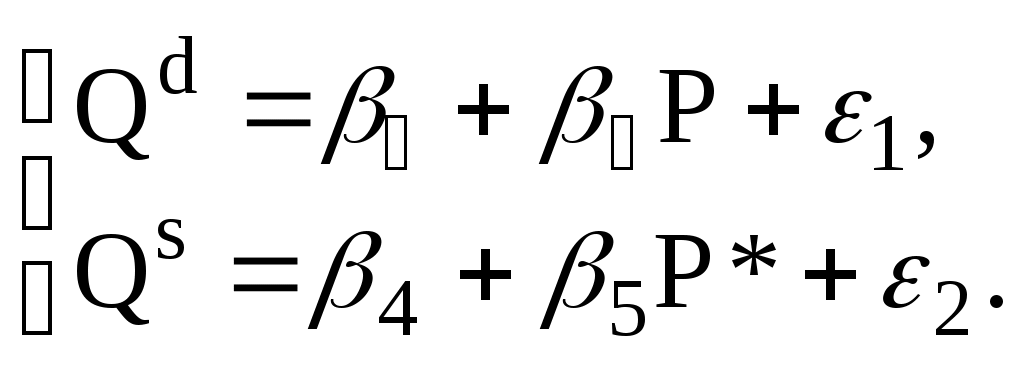 Пример 6. Структурная форма модели имеет вид:  где: Сt– личное потребление в период t, St– зарплата в период t, Pt – прибыль в период t, Rt – общий доход в период t, Rt-1 – общий доход в период t-1, Задание: Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости. Запишите приведенную форму модели. Решение. Модель представляет собой систему одновременных уравнений, состоящую из двух уравнений, которые необходимо проверить на идентифицируемость для определения способа оценки параметров, и тождества, параметры которого известны, поэтому необходимости в проверке его на идентифицируемость нет. Модель включает три эндогенные переменные (Ct, St, Rt) и три экзогенные переменные (Pt, t, в том числе одну лаговую переменную Rt-1). Проверим уравнения модели на идентифицируемость. 1 уравнение. Проверим выполнение необходимого условия идентифицируемости. Это уравнение включает две эндогенные переменные (Ct,St) и одну экзогенную переменную (Pt). Таким образом, H = 2; число экзогенных переменных системы, не входящих в это уравнение, также равно двум D = 2. Получаем: D + 1 > H, следовательно, первое уравнение сверхидентифицируемо. Теперь проверим достаточное условие идентифицируемости. Запишем матрицу коэффициентов при переменных (эндогенных и экзогенных), не входящих в первое уравнение (Rt, Rt-1, t):
Ее ранг равен 2, так как определитель квадратной подматрицы 2х2 этой матрицы не равен нулю: и достаточное условие идентифицируемости выполняется. 2 уравнение. Это уравнение включает две эндогенные переменные (St,Rt) и две экзогенные переменные (Rt-1, t). Таким образом, H = 2; число экзогенных переменных, не входящих в это уравнение, равно одному D = 1. Получаем: D + 1 = H, и второе уравнение является точно идентифицируемым. Теперь проверим достаточное условие идентифицируемости. Запишем матрицу коэффициентов при переменных, не входящих во второе уравнение (Ct, Pt):
Определитель этой матрицы не равен нулю, а ее ранг равен 2: Таким образом, второе уравнение системы точно идентифицируемо. Но так как первое уравнение системы сверхидентифицируемо, то вся модель является сверхидентифицируемой. Запишем приведенную форму модели в общем виде: 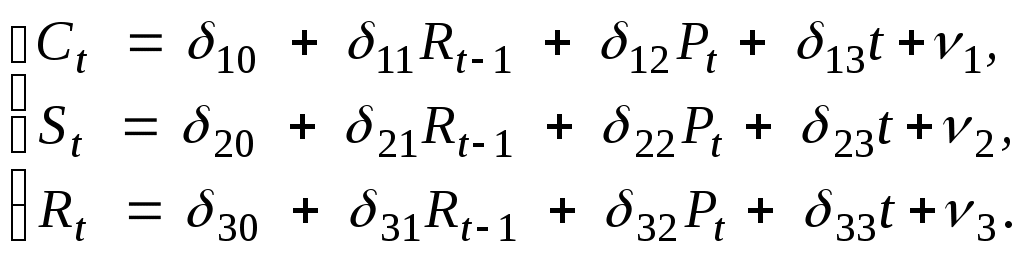 Здесь ν1, ν2, и ν3 - случайные ошибки. Поскольку модель является сверхидентифицируемой, то для оценки параметров уравнений следует применять двухшаговый метод наименьших квадратов. Тема 8. Идентификация систем одновременных уравнений. Наиболее распространенные методы оценки параметров системы одновременных уравнений: косвенный метод наименьших квадратов; двухшаговый метод наименьших квадратов; трехшаговый метод наименьших квадратов; метод максимального правдоподобия с полной информацией; метод максимального правдоподобия при ограниченной информации. Для оценки параметров идентифицируемой системы применяется косвенный метод наименьших квадратов (КМНК), а для оценки коэффициентов сверхидентифицируемой системы применяется двухшаговый метод наименьших квадратов (ДМНК). Процедура применения КМНК состоит из следующих этапов: структурная модель преобразовывается в приведенную форму модели; для каждого уравнения приведенной формы модели оцениваются приведенные коэффициенты (δij) обычным МНК; коэффициенты приведенной формы модели преобразовываются в параметры структурной формы. Основная идея ДМНК – на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. составляется приведенная форма модели, и определяются численные значения параметров каждого уравнения обычным МНК; выявляются эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находятся расчетные значения по соответствующим уравнениям приведенной формы модели; обычным МНК определяются параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения. Таким образом, метод наименьших квадратов применяется дважды: при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических значений эндогенных переменных. ДМНК является более общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнения ДМНК дает тот же результат, что и КМНК, поэтому в ряде компьютерных программ реализован только ДМНК. Трехшаговый метод наименьших квадратов заключается в том, что на первом шаге к исходной модели применяется обобщенный метод наименьших квадратов с целью устранения корреляции случайных членов. Затем к полученным уравнениям применяется двухшаговый метод наименьших квадратов. Если случайные члены в модели не коррелируют, то трехшаговый метод наименьших квадратовсводится к двухшаговому. Пример 7. Рассмотрим систему линейных одновременных уравнений, структурная форма которой приведена в примере 6:  Задание: Определите метод оценки параметров модели. Изложите методику оценки структурных параметров модели. Решение. Проверка модели на идентифицируемость показала, что первое уравнение является сверхидентифицируемым, а второе – точно идентифицируемым (см. пример 6). Следовательно, для оценки параметров первого уравнения следует применять двухшаговый метод наименьших квадратов, а для оценки параметров второго уравнения - косвенный метод наименьших квадратов. Методика оценки параметров первого уравнения. 1. В соответствии со схемой ДМНК на первом этапе запишем приведенную форму модели: 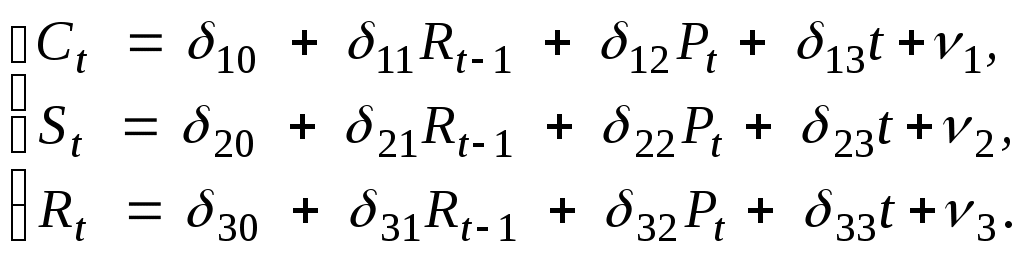 Параметры δij каждого уравнения приведенной формы определяются обычным методом наименьших квадратов. 2. На втором этапе выявляются эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и нахо-дятся расчетные значения по соответствующим уравнениям приведенной формы модели. В нашем примере это переменная St, расчетные значения которой можно определить из второго уравнения приведенной формы модели. 3. В первое структурное уравнение, которое является сверхидентифицируемым, вместо фактических значений переменной St, подставляем расчетные значения Параметры этого уравнения уже можно оценивать обычным методом наименьших квадратов. Методика оценки параметров второго уравнения. Параметры приведенной формы модели δij уже были определены на первом этапе. Сравнивая второе уравнение структурной формы модели и второе уравнение приведенной формы, видно, что для получения соответствия между ними необходимо из второго уравнения приведенной формы исключить переменную Pt и ввести переменную Rt. Для этого из третьего уравнения приведенной формы модели выражаем переменную Pt: Pt = 1/δ32(Rt – δ30 – δ31Rt-1 – δ33t–ν3) и подставляем ее во второе уравнение приведенной формы: St = δ20 + δ21Rt-1 + δ22/δ32(Rt – δ30 – δ31Rt-1 – δ33t–ν3) + δ23t+ν2. Теперь раскрываем скобки: St = δ20 + δ22/δ32∙Rt + (δ21 – δ31δ22/δ32)Rt-1 + (δ23 – δ33δ22/δ32)t+ν2 – δ22/δ32∙ν3. Сопоставляя полученной уравнение со вторым уравнением структурной формы, определяем коэффициенты: a2 = δ20 – δ30/δ32; b21 = δ22/δ32; b22 = δ21 – δ31δ22/δ32; b23 = δ23 – δ33δ22/δ32; ε2 = ν2 – δ22/δ32∙ν3. Таким образом, все параметры структурной формы модели определены. |
