пее. 7. варианты контрольных работ и методические указания по их выполнению

• Название: 7. варианты контрольных работ и методические указания по их выполнению
• Дата: 25.06.2022
• Размер: 1.15 Mb.
• Имя файла: ekonometrika_dlya_zaochnikov.doc
• Тип: Методические указания; #614935
• страница: 1 из 9

7. ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ ВЫПОЛНЕНИЮ

Каждый вариант контрольной работы содержит 3 задачи по основным темам курса эконометрики. Студент выполняет тот вариант контрольной работы, который соответствует начальной букве его фамилии (см. таблицу 1).

Таблица 1.

Начальная буква фамилии студента	Номер варианта контрольной работы
А, Б, В, Г, Д	Вариант 1
Е, Ж, З, И	Вариант 2
К, Л, М	Вариант 3
Н, О, П, Р	Вариант 4
С, Т, У, Ф	Вариант 5
Х, Ц, Ч, Ш, Щ	Вариант 6
Э, Ю, Я	Вариант 7

При выполнении контрольной работы надо соблюдать следующие правила:

1. 
   указывать вариант контрольной работы;
   
2. 
   расчеты производить с помощью компьютерных пакетов (Excel, Statistica, SPSS, и др. по выбору студента);
   
3. 
   представлять решения задач подробно, со всеми формулами, расчетами и пояснениями.
   
4. 
   проверять правильность примененных методов решения задач;
   
5. 
   формулировать четкие, грамотные, обоснованные выводы;
   
6. 
   в конце контрольной работы необходимо привести перечень использованной литературы и поставить свою личную подпись;
   
7. 
   кроме распечатанного варианта контрольной работы необходимо представить дискету с файлом расчетов.
   

Контрольная работа, выполненная не по своему варианту, не зачитывается.

Выполненная контрольная работа представляется в университет для рецензирования. Правильно выполненная работа зачитывается. Если по зачтенной работе рецензентом будут сделаны замечания, необходимо разобраться в них, внести требуемые исправления и представить соответствующие доработки преподавателю.

Студенты, не получившие зачет по контрольной работе, к сдаче экзамена не допускаются. На экзамене студенты должны быть готовы ответить на вопросы преподавателя по решению задач контрольной работы.
Тема 1. Задачи эконометрики в области социально-экономических исследований. Основные этапы эконометрического моделирования.

Название «эконометрика», введенное норвежским экономистом и статистиком Рагнаром Фришем, в буквальном переводе означает «измерения в экономике». Единое общепринятое определение эконометрики в настоящее время отсутствует, поэтому приведем высказывания известных ученых, дающие представление об этой науке.

«Эконометрика – это раздел экономики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными» (Р.Фишер и др.)

Э.Маленво интерпретировал эконометрику как «любое приложение математики или статистических методов к изучению экономических явлений».

Существует и более узкая трактовка эконометрики. «Эконометрика - самостоятельная экономико-математическая научная дисциплина, позволяющая на базе положений экономической теории и исходных данных экономической статистики, используя необходимый математико-статистический инструментарий, придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией» (Айвазян С.А., Мхитарян В.С.).

Из сказанного выше следует, что главное назначение эконометрики – модельное описание конкретных количественных взаимосвязей, существующих между анализируемыми показателями.

В соответствии с целями можно выделить две основные задачи, решаемые с помощью эконометрики: прогноз экономических и социально-экономических показателей, характеризующих состояние и развитие изучаемой системы; моделирование возможных сценариев социально-экономического развития изучаемой системы.

Существует три основных класса моделей, которые применяются для анализа или прогноза.

1. 
   Модели временных рядов, включающие модели:
   

- тренда: y(t)= T(t)+_t, где T(t) – временной тренд заданного параметрического вида, _t - случайная компонента;

- сезонности y(t)= S(t)+_t, где S(t) – периодическая (сезонная) компонента, _t - случайная компонента;

- тренда и сезонности y(t)= T(t)+ S(t)+_t, (аддитивная);

y(t)= T(t)·S(t)+_t, (мультипликативная);

2. 
   Регрессионные модели с одним уравнением
   

В таких моделях зависимая переменная y представляется в виде функции y = f(x₁,… , x_n), где x₁, … , x_n - независимые (объясняющие) переменные. В зависимости от вида функции f(x₁,… , x_n) модели делятся на линейные и нелинейные.

3. 
   Системы одновременных уравнений
   

Эти модели описываются системами одновременных уравнений, которые могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы.

Примером системы одновременных уравнений является модель спроса и предложения, когда объем спроса на товар (Q^d) определяется его ценой (P) и доходом потребителя (I), объем предложения (Q^s) – его ценой (P) и достигается равновесие между спросом и предложением: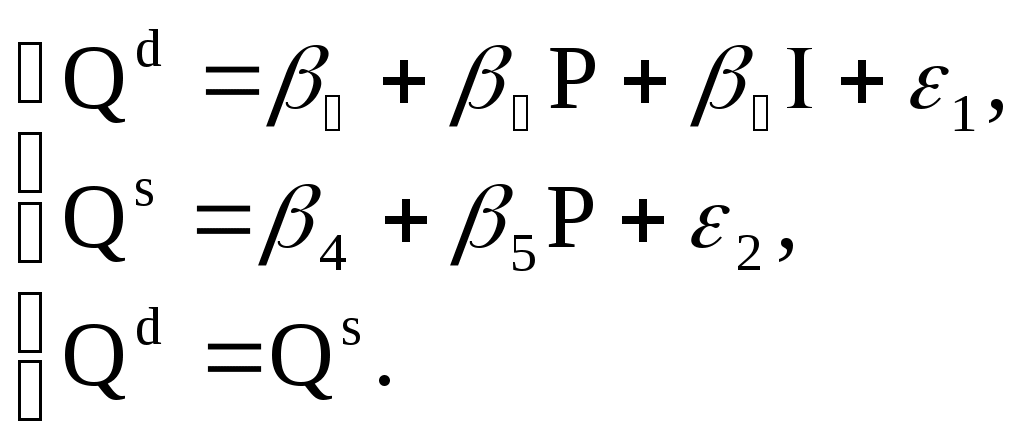



При эконометрическом моделировании мы встречаемся с двумя типами данных: пространственные данные (набор показателей экономических переменных в один и тот же момент времени) и временные ряды (серия наблюдений одной и той же случайной величины в последовательные моменты времени).

Весь процесс эконометрического моделирования можно разделить на шесть основных этапов:

• 
  постановочный (на этом этапе формируется цель исследования, определяется набор участвующих в модели экономических переменных);
  
• 
  априорный (проводится анализ экономической сущности изучаемого объекта, формирование и формализация известной до начала исследования (априорной) информации);
  
• 
  параметризация (осуществляется непосредственно моделирование, т.е. выбор общего вида модели, в том числе состава переменных и формы их связи);
  
• 
  информационный (собирается необходимая статистическая информация -
  наблюдаемые значения экономических переменных);
  
• 
  идентификация модели (на .том этапе проводится статистический анализ модели и оценка ее параметров);
  
• 
  верификация модели (проверяется истинность, адекватность модели, т.е. соответствие моделируемому реальному экономическому объекту).
  

На первых трех этапах весьма важной является проблема спецификации модели, включающая выражение в математической форме выявленных связей и соотношений, установление состава объясняющих переменных (в том числе и лаговых), формулировка исходных предпосылок и ограничений модели и ряд других вопросов. Спецификация опирается на имеющиеся экономические теории, специальные знания, а также на интуитивные представления об анализируемом экономическом объекте.

От проблемы идентификации модели (которая заключается в выборе и реализации методов статистического оценивания ее неизвестных параметров) следует отличать проблему ее идентифицируемости, т.е. проблему возможности получения однозначно определенных параметров модели, заданной системой одновременных уравнений.

Широкому внедрению эконометрических методов способствовало развитие информационных технологий. Компьютерные эконометрические пакеты сделали эти методы более доступными. Наиболее трудоемкая работа по вычислению различных статистик, параметров, построению таблиц и графиков в основном выполняется компьютером, а исследователю остается работа по постановке задачи, выбору соответствующей модели и метода ее решения, а также интерпретации результатов.
Тема 2. Классическая и обобщенная линейные модели множественной
регрессии.

Экономические явления определяются, как правило, большим числом совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной переменной Y от нескольких объясняющих переменных X₁, X₂, …,X_n. Эта задача решается с помощью множественного регрессионного анализа.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, включающего отбор факторов и выбор вида уравнения регрессии. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

• 
  они должны быть количественно измеримы (качественным факторам необходимо придать количественную определенность);
  
• 
  между факторами не должно быть высокой корреляционной, а тем более функциональной зависимости, т.е. наличия мультиколлинеарности.
  

Включение в модель мультиколлинеарных факторов может привести к следующим последствиям:

• 
  затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом виде», поскольку факторы связаны между собой; параметры линейной регрессии теряют экономический смысл;
  
• 
  оценки параметров ненадежны, имеют большие стандартные ошибки и меняются с изменением объема наблюдений.
  

Пусть Y=(y₁, y₂, …,y_n)^т – матрица-столбец значений зависимой переменной размера n;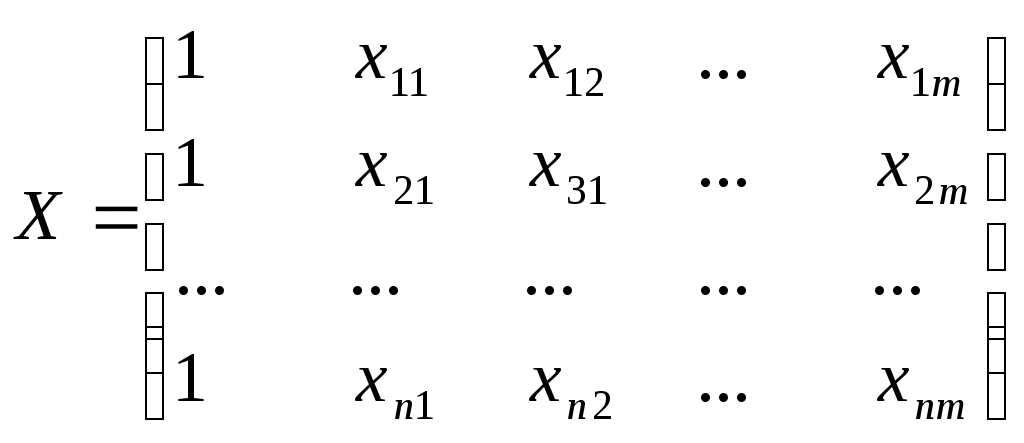

– матрица значений объясняющих переменных;

β=(β₀, β₁, …,β_m)^т – матрица-столбец (вектор) параметров размера m+1;

ε=(ε₁, …,ε_n)^т – матрица-столбец (вектор) остатков размера n.

Тогда в матричной форме модель множественной линейной регрессии запишется следующим образом:

Y = Xβ + ε. (1)

Оценка этой модели по выборке:

Y = Xb + e, (2)

где b=(b₀, b₁, …,b_m)^т – матрица-столбец (вектор) оценок параметров размера

Для оценки параметров уравнения регрессии (вектора b) применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки:

1. 
   В модели (1) ε – случайный вектор, X – неслучайная (детерминированная) матрица.
   
2. 
   Математическое ожидание величины остатков равно нулю: М(ε)=0_n.
   
3. 
   Дисперсия остатков ε_iпостоянна для любого i (условие гомоскедастичности), остатки ε_iи ε_j при i≠j не коррелированы: М(εε^Т)=σ²E_n.
   
4. 
   ε – нормально распределенный случайный вектор, т.е. εN(0_n; σ²E_n).
   
5. 
   r(X) = m+1<n. Столбцы матрицы Х должны быть линейно независимыми (ранг матрицы Х максимальный, а число наблюдений n превосходит ранг матрицы).
   

Модель (1), в которой зависимая переменная, остатки и объясняющие переменные удовлетворяют предпосылкам 1-5 называется классической нормальной линейной моделью множественной регрессии. Если не выполняется только предпосылка 4, то модель называется классической линейной моделью множественной регрессии (КЛММР).

Согласно методу наименьших квадратов неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений фактических значений от значений, найденных по уравнению регрессии, была минимальной:

(Y-Xb)(Y-Xb)^Т → min

Решением этой задачи является вектор b = (X^ТX)^-1X^ТY.

Полученная оценка параметров модели должна быть несмещенной, состоятельной и эффективной, то есть иметь наименьшее рассеяние относительно оцениваемого параметра. По теореме Гаусса-Маркова при выполнении предпосылок регрессионного анализа оценка метода наименьших квадратов b = (X^ТX)^-1X^ТY является наиболее эффективной, то есть обладает наименьшей дисперсией в классе линейных несмещенных оценок.

Оценка адекватности модели множественной регрессии.

Одной из наиболее эффективных оценок адекватности модели является коэффициент детерминации R², определяемый формулой: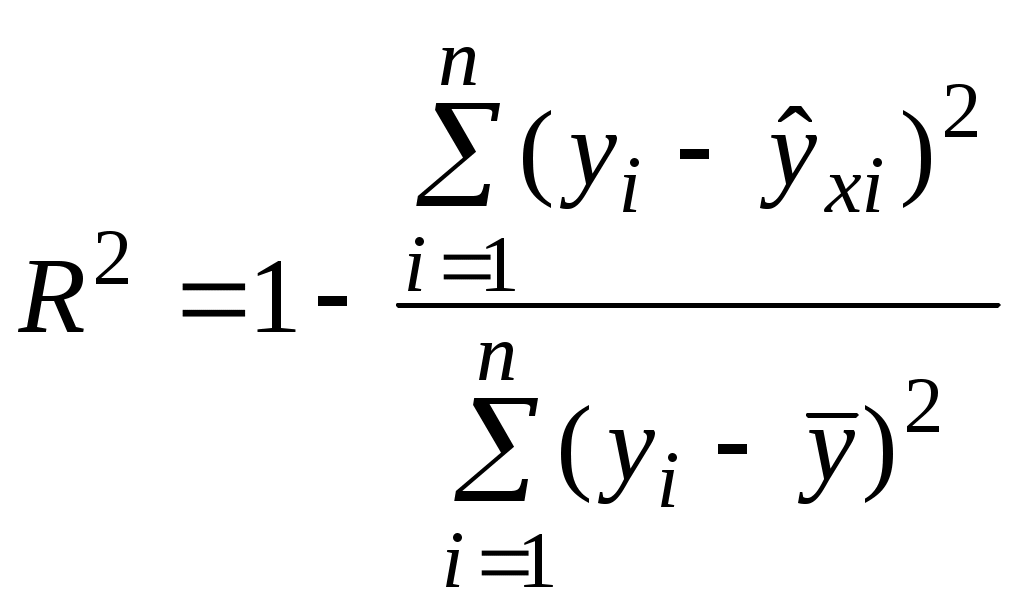

.

Коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных. Чем ближе R² к единице, тем лучше построенная регрессионная модель описывает зависимость между объясняющими и зависимой переменной.

Следует иметь в виду, что при включении в модель новой объясняющей переменной, коэффициент детерминации увеличивается, хотя это и не обязательно означает улучшение качества регрессионной модели. В этой связи лучше использовать скорректированный (поправленный) коэффициент детерминации , рассчитываемый по формуле:

,

где n – число наблюдений,

m – число параметров при переменных x.

Из формулы следует, что с включением в модель дополнительных переменных разница между значениями и R² увеличивается. Таким образом, скорректированный коэффициент детерминации может уменьшаться при добавлении в модель новой объясняющей переменной, не оказывающей существенного влияния на результативный признак.

Но использование только коэффициента детерминации для выбора наилучшего уравнения регрессии может оказаться недостаточным.
Средняя относительная ошибка аппроксимации рассчитывается по формуле:

.

Значимость уравнения регрессии в целом сводится к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при факторных признаках, т.е. гипотезы:

Н₀: b₁ = b₂ =…= b_m =0.

Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех факторных признаков х₁, х₂,… х_m, включенных в модель, на зависимую переменную y можно считать статистически несущественным. Проверка данной гипотезы осуществляется на основе дисперсионного анализа.

Основной идеей дисперсионного анализа является разложение общей суммы квадратов отклонений результативной переменной y от среднего значения на «объясненную» и «остаточную»:

.

Общая сумма квадратов отклонений

Сумма квадратов отклонений, объясненная регрессией

Остаточная сумма квадратов отклонений

Для приведения дисперсий к сопоставимому виду, определяют дисперсии на одну степень свободы. Результаты вычислений заносят в специальную таблицу дисперсионного анализа:

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Оценка дисперсии на одну степень свободы
Объясненная		m
Остаточная		n – m – 1
Общая		n – 1	-

В данной таблице n – число наблюдений, m – число параметров при переменных x.

Сравнивая полученные оценки объясненной и остаточной дисперсии на одну степень свободы, определяют значение F-критерия Фишера, используемого для оценки значимости уравнения регрессии:

.

С помощью F-критерия проверяется нулевая гипотеза о равенстве дисперсий Н₀: s_R² = s².

Если нулевая гипотеза справедлива, то объясненная и остаточная дисперсии не отличаются друг от друга. Для того, чтобы уравнение регрессии было значимо в целом (гипотеза Н₀ была опровергнута) необходимо, чтобы объясненная дисперсия превышала остаточную в несколько раз. Критическое значение F-критерия определяется по таблице Фишера-Снедекора.

Расчетное значение сравнивается с табличным, и если оно превышает табличное (F_расч >F_табл), то гипотеза Н₀отвергается, и уравнение регрессии признается значимым.

Если F_расч табл, то уравнение регрессии считается статистически незначимым. Нулевая гипотеза Н₀не может быть отклонена.

Расчетное значение F-критерия связано с коэффициентом детерминации R²
следующим соотношением:

,

где m – число параметров при переменных x;

n – число наблюдений.

Оценка значимости коэффициентов регрессии сводится к проверке гипотезы о
равенстве нулю коэффициента регрессии при соответствующем факторном признаке,
т.е. гипотезы:

Н₀: b_j =0.

Проверка гипотезы проводится с помощью t-критерия Стьюдента. Для этого определяется расчетное значение t-критерия:

,

где b_j – коэффициент регрессии при x_i;

– средняя квадратическая ошибка коэффициента регрессииb_j.

сравнивается с табличным t_табл при заданном уровне значимости α и числе степеней свободы (n-2).

Если расчетное значение превышает табличное, то гипотезу о несущественности коэффициента регрессии можно отклонить.

Рассмотрим интерпретацию параметров модели линейной множественной регрессии. В линейной модели множественной регрессии =b₀ + b₁∙x₁ + … + b_m∙x_m коэффициенты регрессии b_j характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.

На практике часто бывает необходимо сравнить влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии β_jи коэффициенты эластичности Э_j (j=1, 2, …, m).

Уравнение регрессии в стандартизованной форме:

,

где , – стандартизованные переменные.

В результате такого нормирования средние значения всех стандартизованных переменных равны нулю, а дисперсии равны единице, т.е. = =…= =0, = =…= =1.

Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами следующим соотношением: .

Стандартизованные коэффициенты показывают, на сколько стандартных отклонений (сигм) изменится в среднем результат, если соответствующий фактор x_i изменится на одно стандартное отклонение (одну сигму) при неизменном среднем уровне других факторов. Сравнивая стандартизованные коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат.

Средние коэффициенты эластичности вычисляются по формуле:

.

Коэффициент эластичности показывает, на сколько процентов (от средней) изменится в среднем Y при увеличении только фактора X_j на 1%.
Рассмотрим пример построения модели множественной регрессии с помощью средств приложения Microsoft Excel.
Пример1. По данным, представленным в таблице 2, изучается зависимость балансовой прибыли предприятия торговли  (тыс. руб.) от следующих факторов:

- объем товарных запасов, тыс. руб.;

- фонд оплаты труда, тыс. руб.;

- издержки обращения, тыс. руб.;

- объем продаж по безналичному расчету, тыс. руб.

Таблица 2

Месяц	Y	Х1	Х2	Х3	Х4
	41321,57	300284,10	19321,80	42344,92	100340,02
	40404,27	494107,21	20577,92	49000,43	90001,35
	37222,12	928388,75	24824,91	50314,52	29301,98
	37000,80	724949,11	28324,87	48216,41	11577,42
	29424,84	730855,33	21984,07	3301,30	34209,84
	20348,19	2799881,13	11000,02	21284,21	29300,00
	11847,11	1824351,20	4328,94	28407,82	19531,92
	14320,64	1624500,80	7779,41	40116,00	17343,20
	18239,46	1115300,93	18344,11	32204,98	4391,00
	22901,52	1200947,52	20937,31	30105,29	14993,25
	27391,92	1117850,93	27344,30	40294,40	104300,00
	44808,37	1379590,02	31939,52	42239,79	119804,33
	40629,28	588365,77	29428,60	55584,35	155515,15
	31324,80	434281,91	30375,82	49888,17	60763,19
	34847,92	1428243,59	33000,94	59866,55	8763,25
	33241,32	1412181,59	31322,60	49975,79	4345,42
	29971,34	1448274,10	20971,82	3669,92	48382,15
	17114,90	4074616,71	11324,93	26032,95	10168,00
	8944,94	1874298,99	8341,52	29327,21	22874,40
	17499,58	1525436,47	10481,14	40510,01	29603,05
	19244,80	1212238,89	18329,90	37444,69	16605,16
	34958,32	1154327,22	29881,52	36427,22	32124,63
	44900,83	1173125,03	34928,60	51485,62	200485,00
	57300,25	1435664,93	41824,92	49959,92	88558,62

Задание:

1. 
   Для заданного набора данных постройте линейную модель множественной
   регрессии.
   
2. 
   Оцените точность и адекватность построенного уравнения регрессии.
   
3. 
   Выделите значимые и незначимые факторы в модели.
   
4. 
   Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
   

Решение.

Для получения отчета по построению модели в среде EXCEL необходимо выполнить следующие действия:

1. 
   В меню Данные выбираем команду Анализ данных. На экране появится окно