пее. 7. варианты контрольных работ и методические указания по их выполнению
 Скачать 1.15 Mb.
|
|
Тема 3. Линейные регрессионные модели с переменной структурой. При изучении социально-экономических процессов и явлений может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровня, например, образование, пол, фактор сезонности. Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным. Оценить влияние значений количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии можно путем введения фиктивных переменных. В качестве фиктивных переменных обычно используются дихотомические (бинарные) переменные, которые принимают всего два значения: «0» и «1». Например, при исследовании зависимости заработной платы от уровня образования Z можно рассмотреть k=3 уровня: начальное образование, среднее и высшее. Обычно вводят (k-1) бинарную переменную. В нашем случае потребуется ввести две фиктивные переменные. Тогда регрессионная модель запишется в виде: y= b0 + b1∙x1 + … + bm∙xm + bm+1∙z1 + bm+2∙z2 +ε, где   x1, …,∙xm – экономические (количественные) переменные. Наличие у работника начального образования будет отражено парой значений z1=0, z2=0. Параметры при фиктивных переменных z1 и z2 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы (в нашем примере это работники с начальным образованием). При построении регрессионных моделей по неоднородным данным необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле, можно ли объединить их в одну и рассматривать единую модель регрессии? Для ответа на этот вопрос можно воспользоваться тестом Г.Чоу. По каждой выборке строятся две линейные регрессионные модели: 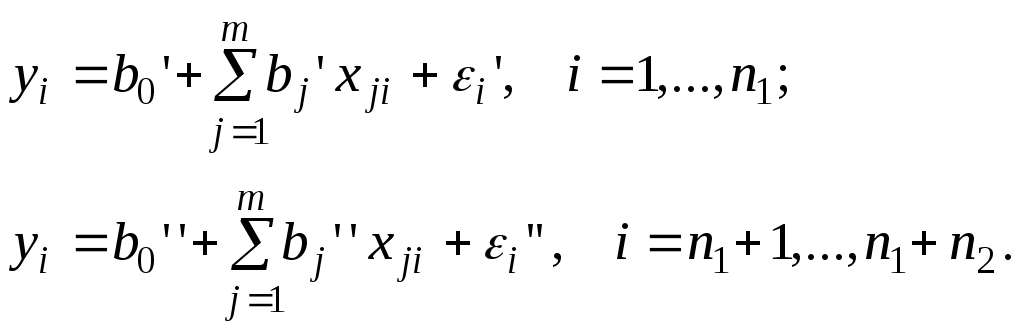 Проверяемая нулевая гипотеза имеет вид – H0: b'=b''; D(ε')= D(ε'')= σ2. Если нулевая гипотеза верна, то две регрессионные модели можно объединить в одну объема n = n1 + n2. Согласно критерию Г.Чоу нулевая гипотеза H0 отвергается на уровне значимости α, если статистика  где 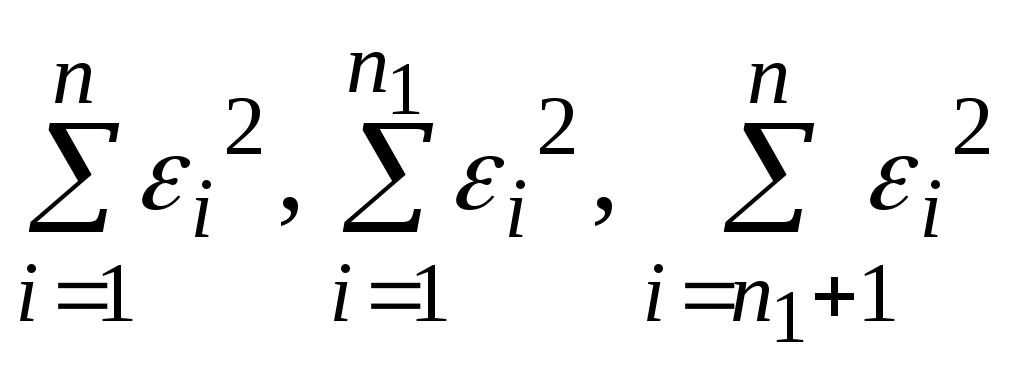 - остаточные суммы квадратов соответственно для объединенной, первой и второй выборок, n = n1 + n2.Для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда можно также использовать тест Д.Гуйарати. Пример 4. Рассмотрим полученную в примере 1 модель зависимости балансовой прибыли предприятия торговли  (тыс. руб.) от следующих переменных: - фонд оплаты труда, тыс. руб.;  - объем продаж по безналичному расчету, тыс. руб.Известно, что первая выборка значений переменных объемом n1=12 получена при одних условиях, а другая, объемом n2=12, - при несколько измененных условиях. Задание: Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки в одну и рассматривать единую модель регрессии по  ?Решение. Для проверки предположения об однородности исходных данных в регрессионном смысле применим тест Чоу. В соответствии со схемой теста построим уравнения регрессии по первым n1=12 наблюдениям. Результаты представлены в таблице 8. Таблица 8
Результаты дисперсионного анализа модели, построенной по оставшимся n2=12 наблюдениям, представлены в таблице 9. Таблица 9
Результаты регрессионного и дисперсионного анализа модели, построенной по всем n =n1 + n2 = 24 наблюдениям, представлены в таблице 3 (ESS = 6,39Е+08): Рассчитаем статистику F по формуле:  .Находим табличное значение Fтабл= FРАСПОБР(0,05;3;18) = 3,15. Так как, Fрасч< Fтабл, то справедлива гипотеза  , т.е. надо использовать единую модель по всем наблюдениям. Тема 4. Нелинейные модели регрессии и их линеаризация. Довольно часто соотношения между социально-экономическими явлениями и процессами приходится описывать нелинейными функциями. Например, производственные функции (зависимость между объемом производства и основными факторами производства) или функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом). Следует различать модели, нелинейные по параметрам, и модели, нелинейные по переменным. Для оценки параметров нелинейных моделей существует два основных подхода: 1. Первый подход основан на линеаризации модели: преобразованием исходных переменных и введением новых, нелинейную модель можно свести к линейной, для оценки параметров которой используется метод наименьших квадратов. 2. Если подобрать соответствующее линеаризующее преобразование не удается, то применяются методы нелинейной оптимизации на основе исходных переменных. Если модель нелинейна по переменным, то используется первый подход, т.е. вводятся новые переменные, и модель сводится к линейной: y =  + ε.Переходим к новым переменным: x1'=lnx1, x2'=  и получаем линейное уравнение:y =  + ε.Более сложной проблемой является нелинейность по оцениваемым параметрам. В ряде случаев путем подходящих преобразований эти модели удается привести к линейному виду. Рассмотрим следующие модели, нелинейные по оцениваемым параметрам: степенная (мультипликативная) –  ,Степенная модель может быть преобразована к линейной путем логарифмирования обеих частей уравнения: lny = ln  + lnε.Замена переменных: y'=lny, b0'=lnb0, x1'=lnx1, …, xm'=lnxm, ε'=lnε. В новых переменных модель запишется следующим образом: y' =  + ε'.Степенные модели получили широкое распространение в эконометрическом моделировании ввиду простой интерпретации параметров, которые представляют собой частные коэффициенты эластичности результативного признака по соответствующим факторным признакам. экспонента –  ,Экспоненциальная модель линеаризуется аналогично: lny =  + lnε.Переходя к новым переменным y'=lny, ε'=lnε, получаем линейную регрессионную модель: y' = + ε'.гипербола –  .Гиперболическая модель линеаризуется непосредственной заменой переменной y'=1/y: y' = + ε.Эти функции используются при построении кривых Энгеля, которые описывают зависимость спроса на определенный вид товаров или услуг от уровня доходов потребителей или от цены товара. логарифмическая модель: y = + ε.При выборе формы уравнения регрессии важно помнить, что чем сложнее функция, тем менее интерпретируемы ее параметры. В качестве примера использования линеаризующего преобразования регрессии рассмотрим производственную функцию Кобба-Дугласа: Y = AKαLβε, где Y – объем производства, К – затраты капитала, L – затраты труда. Путем логарифмирования обеих частей данную степенную модель можно свести к линейной: lnY = lnA + α·lnK + β·lnL + lnε. Переходя к новым переменным Y'=lnY, A'=lnA, K'=lnK, L'=lnL, ε'=lnε, получаем линейную регрессионную модель: Y' = A' + α·K' + β·L' + ε'. Эластичность выпуска продукции. Показатели αиβявляются коэффициентами частной эластичности объема про-изводства Y соответственно по затратам капитала К и труда L. Это означает, что с увели-чением только затрат капитала (труда) на 1% объем производства возрастает на α% (β%): 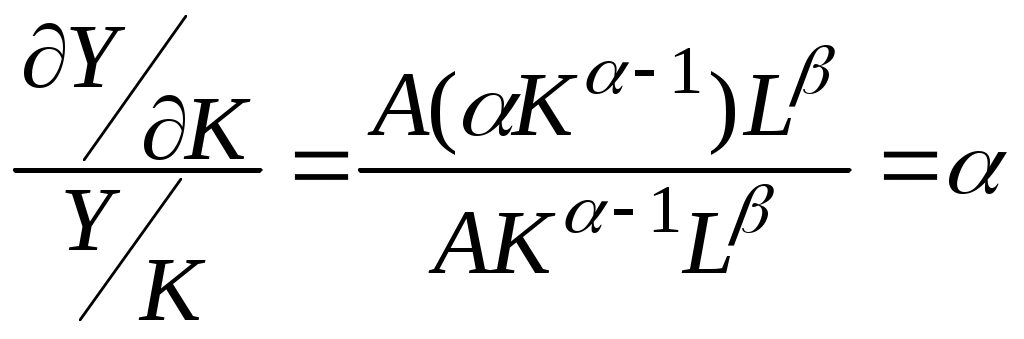 ; .Эффект от масштаба производства. Если α и β в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то Y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства. Если их сумма меньше единицы, то имеет место убывающий эффект от масштаба производства. Например, К и L увеличиваются в 2 раза. Найдем новый уровень выпуска (Y*): Y* = A(2K)α(2L)β = A2αKα2βLβ = 2α+βAKαLβ= 2α+βY. Если α+β =1,2, то 2α+β=2,30, а Yувеличивается больше, чем в 2 раза. Если α+β =1, то 2α+β=2, и Yувеличивается также в 2 раза. Если α+β =0,8, то 2α+β=1,74, а Yувеличивается меньше, чем в 2 раза. Первоначально Кобб и Дуглас представляли функцию в виде Y = AKαL1-αε, т.е. предполагали постоянную отдачу от масштаба производства. Впоследствии это допущение было ослаблено. Если в модели α+β =1, то функцию Кобба-Дугласа представляют в виде Y = AKαL1-αε или  .Таким образом, переходят к зависимости производительности труда (Y/L) от его капиталовооруженности (К/L). Логарифмируя обе части уравнения, приводим его к линейному виду: ln(Y/L) = lnA + α·ln(К/L) + lnε. Функция Кобба-Дугласа с учетом технического прогресса имеет вид: Y = AKαLβeθtε, где t – время, параметр θ – темп прироста объема производства благодаря техническому прогрессу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||