пее. 7. варианты контрольных работ и методические указания по их выполнению
 Скачать 1.15 Mb.
|
Рис. 1.В появившемся окне выбираем пункт Регрессия. Появляется диалоговое окно, в котором задаем необходимые параметры (рис. 2).  Рис. 2.Диалоговое окно рис. 2 заполняется следующим образом: Входной интервал  – диапазон (столбец), содержащий данные со значениями объясняемой переменной;Входной интервал  – диапазон (столбцы), содержащий данные со значениями объясняющих переменных. Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет; Константа-ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении регрессии (  );Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели; Новый рабочий лист – можно задать произвольное имя нового листа, в котором будет сохранен отчет. Если необходимо получить значения и графики остатков (  ), установите соответствующие флажки в диалоговом окне. Нажмите на кнопку OK.Вид отчета о результатах регрессионного анализа представлен на рис. 3.  Рис. 3. Рассмотрим таблицу "Регрессионная статистика". Множественный R – это  , где  – коэффициент детерминации.R-квадрат – это  . В нашем примере значение = 0,8178 свидетельствует о том, что изменения зависимой переменной (балансовой прибыли) в основном (на 81,78%) можно объяснить изменениями включенных в модель объясняющих переменных – Х1, Х2, Х3, Х4. Такое значение свидетельствует об адекватности модели.Нормированный R-квадрат – поправленный (скорректированный по числу степеней свободы) коэффициент детерминации. Стандартная ошибка регрессии  , где  – необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии); n – число наблюдений (в нашем примере равно 24), m – число объясняющих переменных (в нашем примере равно 4). Наблюдения – число наблюдений n. Рассмотрим таблицу с результатами дисперсионного анализа. df – degrees of freedom – число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант (m+1). SS – sum of squares – сумма квадратов (регрессионная (RSS –regression sum of squares), остаточная (ESS – error sum of squares) и общая (TSS – total sum of squares), соответственно). MS – meansum - сумма квадратов на одну степень свободы. F - расчетное значение F-критерия Фишера. Если нет табличного значения, то для проверки значимости уравнения регрессии в целом можно посмотреть Значимость F. На уровне значимости  уравнение регрессии признается значимым в целом, если Значимость  , и незначимым, если Значимость  .Для нашего примера имеем следующие значения:
В нашем случае расчетное значение F-критерия Фишера составляет 21,32. Значимость F = 8,28Е-07, что меньше 0,05. Таким образом, полученное уравнение в целом значимо. В последней таблице приведены значения параметров (коэффициентов) модели, их стандартные ошибки и расчетные значения t-критерия Стьюдента для оценки значимости отдельных параметров модели.
Анализ таблицы для рассматриваемого примера позволяет сделать вывод о том, что на уровне значимости значимыми оказываются лишь коэффициенты при факторах Х2 и Х4. , так как только для них Р-значение меньше 0,05. Таким образом, факторы Х1 и Х3. не существенны, и их включение в модель нецелесообразно.Поскольку коэффициент регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, как например, -0,1948  0,2135. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. Это также подтверждает вывод о статистической незначимости коэффициентов регрессии при факторах Х1 и Х3.Исключим несущественные факторы Х1 и Х3 и построим уравнение зависимости (балансовой прибыли) от объясняющих переменных Х2, и Х4. Результаты регрессионного анализа приведены в таблице 3.Таблица 3
Оценим точность и адекватность полученной модели. Значение = 0,8144 свидетельствует о том, что вариация зависимой переменной (балансовой прибыли) по-прежнему в основном (на 81,44%) можно объяснить вариацией включенных в модель объясняющих переменных – Х2, и Х4. Это свидетельствует об адекватности модели.Значение поправленного коэффициента детерминации (0,7967) возросло по сравнению с первой моделью, в которую были включены все объясняющие переменные (0,7794). Стандартная ошибка регрессии во втором случае меньше, чем в первом (5515 < 5745). Расчетное значение F-критерия Фишера составляет 46,08. Значимость F = 2,08847E-08, что меньше 0,05. Таким образом, полученное уравнение в целом значимо. Далее оценим значимость отдельных параметров построенной модели. Из таблицы 3 видно, что теперь на уровне значимости все включенные в модель факторы являются значимыми: Р-значение < 0,05.Границы доверительного интервала для коэффициентов регрессии не содержат противоречивых результатов: с надежностью 0,95 (c вероятностью 95%) коэффициент b1 лежит в интервале 0,64 ≤ b1 ≤ 1,19; с надежностью 0,95 (c вероятностью 95%) коэффициент b2 лежит в интервале 0,01 ≤ b2 ≤ 0,12 Таким образом, модель балансовой прибыли предприятия торговли запишется в следующем виде:  Рассмотрим теперь экономическую интерпретацию параметров модели. Коэффициентb1 = 0,916, означает, что при увеличении только фонда оплаты труда (Х2) на 1 тыс. руб. балансовая прибыль в среднем возрастает на 0,916 тыс. руб., а то, что коэффициент b2 = 0,065, означает, что увеличение только объема продаж по безналичному расчету (Х4) на 1 тыс. руб. приводит в среднем к увеличению балансовой прибыли на 0,065 тыс. руб. Как было отмечено выше, анализ P-значений показывает, что оба коэффициента значимы. При эконометрическом моделировании реальных экономических процессов предпосылки КЛММР нередко оказываются нарушенными: дисперсии остатков модели не одинаковы (гетероскедастичность остатков), или наблюдается корреляция между остатками в разные моменты времени (автокоррелированные остатки). Тогда предпосылка 3 запишется следующим образом: 3. М(εεТ)=Ω, где Ω – положительно определенная матрица. Принимая, что дисперсии объясняющих переменных могут быть произвольными, мы получаем обобщенную линейную модель множественной регрессии (ОЛММР). В этом случае оценка параметров модели методом наименьших квадратов даст неэффективную оценку, поэтому следует применять обобщенный метод наименьших квадратов (ОМНК). Теорема Айткена. В классе линейных несмещенных оценок вектора β для обобщенной регрессионной модели оценка b* =(XТΩ-1X)-1XТΩ-1Y имеет наименьшую ковариационную матрицу. Если модель гетероскедастична, то матрица Ω – диагональная. Тогда имеем: b* =(XТΩX)-1XТΩY. В этом случае обобщенный метод наименьших квадратов называется взвешенным методом наименьших квадратов, поскольку мы «взвешиваем» каждое наблюдение с помощью коэффициента 1/σi. На практике, однако, значения σi почти никогда не бывают известны. Поэтому сначала находят оценку вектора параметров обычным методом наименьших квадратов. Затем находят регрессию квадратов остатков на квадратичные функции объясняющих переменных, т.е. уравнение е2i =f(xi) + ui, i= 1, …, n, где f(xi) – квадратичная функция. Далее по полученному уравнению рассчитывают теоретические значения  и определяют набор весов  . Затем вводят новые переменные Y*i = Y/σi, X*ji = Xji/σi, (j = 1,…,m; i = 1,…, n) и находят уравнение  . Полученная оценка и есть оценка взвешенного метода наименьших квадратов.Проверить модель на гетероскедастичность можно с помощью следующих тестов: ранговой корреляции Спирмена; Голдфельда-Квандта; Уайта; Глейзера. Рассмотрим тест на гетероскедастичность, применяемый в случае, если ошибки регрессии можно считать нормально распределенными случайными величинами, – тест Голдфельда-Квандта. Все n наблюдений упорядочиваются в порядке возрастания значений фактора X. Затем выбираются m первых и m последних наблюдений. Гипотеза о гомоскедастичности равносильна тому, что значения остатков e1,…,em и en-m+1,…,en представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии. Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью F-критерия Фишера. Расчетное значение вычисляется по формуле (в числителе всегда бо́льшая сумма квадратов):  .Гипотеза о равенстве дисперсий двух наборов по m наблюдений (т.е. гипотеза об отсутствии гетероскедастичности остатков) отвергается, если расчетное значение превышает табличное F >Fα;m-p;m-p, где p – число регрессоров. Мощность теста (вероятность отвергнуть гипотезу об отсутствии гетероскедастичности, когда гетероскедастичности действительно нет) максимальна, если выбирать m порядка n/3. Тест Голдфельда-Квандта позволяет выявить факт наличия гетероскедастичности, но не позволяет описать характер зависимостей дисперсий ошибок регрессии количественно. Если прослеживается влияние результатов предыдущих наблюдений на результаты последующих, случайные величины (ошибки) εi в регрессионной модели не оказываются независимыми. Такие модели называются моделями с наличием автокорреляции. Как правило, если автокорреляция присутствует, то наибольшее влияние на последующее наблюдение оказывает результат предыдущего наблюдения. Наличие автокорреляции между соседними уровнями ряда можно определить с помощью теста Дарбина-Уотсона. Расчетное значение определяется по следующей формуле:  .Затем по таблицам находятся пороговые значения dв и dн. Если расчетное значение: dв< d <4-dв, то гипотеза об отсутствии автокорреляции не отвергается (принимается); dн< d <dв, или 4-dв< d <4-dн, то вопрос об отвержении или принятии гипотезы остается открытым (расчетное значение попадает в зону неопределенности); 0< d <dн, то принимается альтернативная гипотеза о наличии положительной автокорреляции; 4-dн< d <4, то принимается альтернативная гипотеза о наличии отрицательной автокорреляции. Недостаток теста Дарбина-Уотсона заключается прежде всего в том, что он содержит зоны неопределенности. Во-вторых, он позволяет выявить наличие автокорреляции только между соседними уровнями, тогда как автокорреляция может существовать и между более отдаленными наблюдениями. Поэтому наряду с тестом Дарбина-Уотсона для проверки наличия автокорреляции используются тест серий (Бреуша-Годфри), Q-тест Льюинга-Бокса и другие. Наиболее распространенным приемом устранения автокорреляции во временных рядах является построение авторегрессионных моделей. Пример 2. Рассмотрим полученную в предыдущем примере модель зависимости балансовой прибыли предприятия торговли (тыс. руб.) от следующих переменных: - фонд оплаты труда, тыс. руб.; - объем продаж по безналичному расчету, тыс. руб.Задание: Для полученной модели проверьте выполнение условия гомоскедастичности остатков, применив тест Голдфельда-Квандта. Решение. Для выполнения этого задания снова воспользуемся "Пакетом анализа", встроенным в EXCEL. В соответствии со схемой теста Голдфельда-Квандта упорядочим данные по возрастанию переменной Х4, предполагая, что дисперсии ошибок зависят от величины этой переменной. В нашем примере m = n/3 = 8. Результаты дисперсионного анализа модели множественной регрессии, построенной по первым 8 наблюдениям (после ранжирования по возрастанию переменной Х4), приведены в таблице 4. Таблица 4
Результаты дисперсионного анализа модели, построенной по последним 8 наблюдениям, приведены в таблице 5. Таблица 5
Рассчитаем статистику Fрасч = ESS2/ESS1 (т.к. ESS2>ESS1). Для нашего примера получаем: F = 3,98E+08/6,04E+07= 6,58. Для того, чтобы узнать табличное значение, воспользуемся встроенной в EXCEL функцией FРАСПОБР(0,05;6;6) с параметрами 0,05 – заданная вероятность ошибки гипотезы  ; m-p = 8-2 = 6; m-p = 6 – параметры распределения Фишера. Данная функция находится в категории «статистических» функций.Статистика Fрасч больше табличного значения F= FРАСПОБР(0,05;6;6) = 4,28. Следовательно, модель гетероскедастична. Пример 3. Рассмотрим полученную в примере 1 модель зависимости балансовой прибыли предприятия торговли (тыс. руб.) от следующих переменных: - фонд оплаты труда, тыс. руб.; - объем продаж по безналичному расчету, тыс. руб.Задание: Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона. Решение. Прежде всего, по эмпирическим данным необходимо методом наименьших квадратов построить уравнение регрессии и определить значения отклонений  для каждого наблюдения i (i = 1, 2, …, n). Для этого в диалоговом окне Регрессия в группе Остатки следует установить одноименный флажок Остатки. Затем рассчитываем статистику Дарбина-Уотсона по формуле: 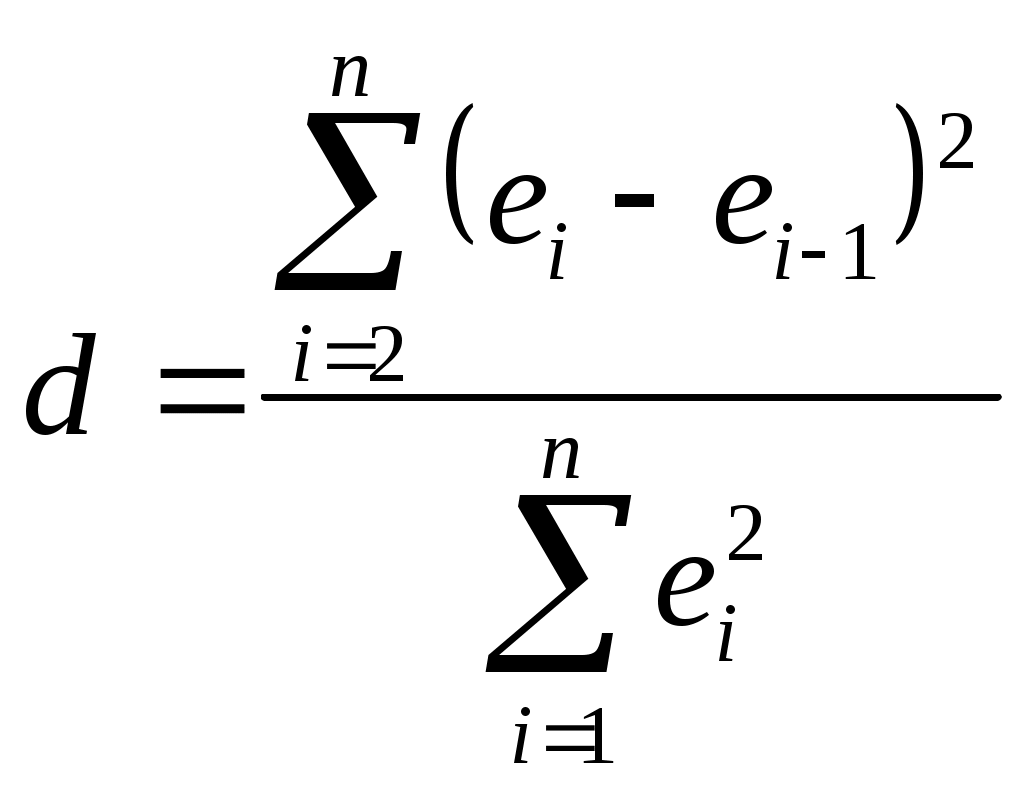 .Результаты расчетов представлены в таблице 6. Таблица 6
Таким образом, расчетное значение равно d = 6,5E+08/ 6,4E+08 = 1,02. По таблице критических точек распределения Дарбина–Уотсона для заданного уровня значимости  , числа наблюдений  и количества объясняющих переменных m определить два значения: dн- нижняя граница и dв - верхняя граница (таблица 7). Таблица 7
В нашем случае модель содержит 2 объясняющие переменные (m=2), нижняя и верхняя границы равны соответственно dн = 1,19 и dв = 1,55. Расчетное значение d-статистики лежит в интервале 0≤d≤dн. Следовательно, в ряду остатков существует положительная автокорреляция. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2,82Е+09
3,30Е+07
5350,78
19024,83
0,00172
0,0026
0,15891
1,2132
0,09754 
0,02647
0,1171