пее. 7. варианты контрольных работ и методические указания по их выполнению

• Название: 7. варианты контрольных работ и методические указания по их выполнению
• Дата: 25.06.2022
• Размер: 1.15 Mb.
• Имя файла: ekonometrika_dlya_zaochnikov.doc
• Тип: Методические указания; #614935
• страница: 6 из 9

Задание:

1. 
   Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
   
2. 
   Выделите значимые и незначимые факторы в модели. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
   
3. 
   Рассчитайте стандартизованные коэффициенты модели и запишите уравнение регрессии в стандартизованном виде. Упорядочите факторы по степени влияния на оборот розничной торговли?
   
4. 
   Для полученной модели проверьте выполнение условия гомоскедастичности
   остатков, применив тест Голдфельда-Квандта.
   
5. 
   Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
   
6. 
   Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки (по первым 12 и остальным
   наблюдениям) в одну и рассматривать единую модель регрессии Y по X?
   

Задача 2.

Модель макроэкономической производственной функции описывается следующим уравнением:

lnY = -3,52 + 1,53lnK + 0,47lnL + ε , R² = 0,875.

(2,43) (0,55) (0,09) F = 237,4

В скобках указаны значения стандартных ошибок для коэффициентов регрессии.

Задание:

1. 
   Оцените значимость коэффициентов модели по t-критерию Стьюдента и сделайте вывод о целесообразности включения факторов в модель.
   
2. 
   Запишите уравнение в степенной форме и дайте интерпретацию параметров.
   
3. 
   Можно ли сказать, что прирост ВНП в большей степени связан с приростом затрат капитала, нежели с приростом затрат труда?
   

Задача 3.

Структурная форма модели имеет вид:



где: C_t– совокупное потребление в период t,

Y_t– совокупный доход в период t,

I_t – инвестиции в период t,

Т_t – налоги в период t,

G_t – государственные расходы в период t,

Y_t-1 – совокупный доход в период t-1.

Задание:

1. 
   Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
   
2. 
   Запишите приведенную форму модели.
   
3. 
   Определите метод оценки структурных параметров каждого уравнения.
   

ВАРИАНТ 4.

Задача 1.

По данным за два года изучается зависимость оборота розничной торговли (Y, млрд. руб.) от ряда факторов: - товарные запасы в фактических ценах, млрд. руб.; Х₂ – номинальная заработная плата, руб.; Х₃ – денежные доходы населения, млрд. руб.; Х₄ – официальный курс рубля по отношению к доллару США.

Таблица 13

Месяц	Y	X1	X2	X3	X4
1	72,9	42,1	988	117,7	6,026
2	67,0	36,7	1000	123,8	6,072
3	69,7	37,9	1059	126,9	6,106
4	70,0	39,1	1040	134,1	6,133
5	69,8	39,6	1047	123,1	6,164
6	69,1	39,6	1122	126,7	6,198
7	70,7	38,8	1110	130,4	6,238
8	80,1	44,9	1052	129,3	7,905
9	105,2	42,9	1112	145,4	16,065
10	102,5	41,5	1123	163,8	16,010
11	108,7	46,9	1164	164,8	17,880
12	134,8	50,6	1482	227,2	20,650
13	116,7	48,3	1167	164,0	22,600
14	117,8	46,7	1199	183,7	22,860
15	128,7	50,4	1385	195,8	24,180
16	129,8	51,9	1423	219,4	24,230
17	133,1	54,2	1472	209,8	24,440
18	136,3	54,6	1626	223,3	24,220
19	139,7	54,4	1618	223,6	24,190
20	151,0	54,9	1608	236,6	24,750
21	154,6	57,0	1684	236,6	25,080
22	160,2	58,1	1716	248,6	26,050
23	163,2	63,1	1785	253,4	26,420
24	191,7	68,0	1808	351,4	27,000

Задание:

1. 
   Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
   
2. 
   Выделите значимые и незначимые факторы в модели. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
   
3. 
   Рассчитайте стандартизованные коэффициенты модели и запишите уравнение регрессии в стандартизованном виде. Упорядочите факторы по степени влияния на оборот розничной торговли?
   
4. 
   Для полученной модели проверьте выполнение условия гомоскедастичности
   остатков, применив тест Голдфельда-Квандта.
   
5. 
   Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
   
6. 
   Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки (по первым 12 и остальным наблюдениям) в одну и рассматривать единую модель регрессии Y по X?
   

Задача 2.

По данным о динамике товарооборота (Y, млрд. руб.) и дохода населения
(X, млрд. руб.) была получена следующая модель с распределенными лагами:

Y_t = 0,55∙X_t + 0,25∙X_t-1+ 0,14∙X_t-2 + 0,09∙X_t-3 + ε_t.

(0,06) (0,04) (0,04) (0,03)

В скобках указаны значения стандартных ошибок для коэффициентов регрессии. R² = 0,99.
Задание:

1. 
   Проанализируйте полученные результаты регрессионного анализа.
   
2. 
   Дайте интерпретацию параметров модели: определите краткосрочный и долгосрочный мультипликаторы.
   
3. 
   Определите величину среднего лага и медианного лага.
   

Задача 3.

Одна из модификаций модели спроса-предложения имеет вид:



где: Q_t^d – предложение товара в период t,

Q_t^s – спрос на товар в период t,

P_t – цена товара в период t,

P_t-1 – цена товара в период t-1,

I_t – доход в период t.
Задание:

1. 
   Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
   
2. 
   Запишите приведенную форму модели.
   
3. 
   Определите метод оценки структурных параметров каждого уравнения.
   

ВАРИАНТ 5.

Задача 1.

По данным, представленным в таблице 14, изучается зависимость чистой прибыли предприятия Y (млрд. долл.) от следующих переменных: X₁- оборот капитала,. млрд. долл.; X₂ - численность служащих, тыс. чел.; X₃ - рыночная капитализация компании, млрд. долл.

Таблица 14

№ п/п	Y	Х1	X2	X3
1	0,9	31,3	43	40,9
2	1,7	13,4	64,7	40,5
3	0,7	4,5	24	38,9
4	1,7	10	50,2	38,5
5	2,6	20	106	37,3
6	1,3	15	96,6	26,5
7	4,1	137,1	347	37
8	1,6	17,9	85,6	36,8
9	6,9	165,4	745	36,3
10	0,4	2	4,1	35,3
11	1,3	6,8	26,8	35,3
12	1,9	27,1	42,7	35
13	1,9	13,4	61,8	26,2
14	1,4	9,8	212	33,1
15	0,4	19,5	105	32,7
16	0,8	6,8	33,5	32,1
17	1,8	27	142	30,5
18	0,9	12,4	96	29,8
19	1,1	17,7	140	25,4
20	1,9	12,7	59,3	29,3
21	0,9	21,4	131	29,2
22	1,3	13,5	70,7	29,2
23	2	13,4	65,4	29,1
24	0,6	4,2	23,1	27,9
25	0,7	15,5	80,8	27,2

Задание:

1. 
   Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
   
2. 
   Выделите значимые и незначимые факторы в модели. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
   
3. 
   Рассчитайте стандартизованные коэффициенты модели и запишите уравнение регрессии в стандартизованном виде. Какой фактор оказывает наибольшее влияние на результат?
   
4. 
   Для полученной модели проверьте выполнение условия гомоскедастичности
   остатков, применив тест Голдфельда-Квандта.
   
5. 
   Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
   
6. 
   Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки (по первым 15 и осталь-ным 10 наблюдениям) в одну и рассматривать единую модель регрессии Y по X?
   

Задача 2.

Производственная функция Кобба-Дугласа характеризуется следующим уравнением:

lgY = -0,15 + 0,35lgK + 0,72lgL + ε , R² = 0,97.

(0,43) (0,06) (0,15) F = 254,9

В скобках указаны значения стандартных ошибок для коэффициентов регрессии.

Задание:

1. 
   Оцените значимость коэффициентов модели по t-критерию Стьюдента и сделайте вывод о целесообразности включения факторов в модель.
   
2. 
   Запишите уравнение в степенной форме и дайте интерпретацию параметров.
   
3. 
   Что можно сказать об эффекте от масштаба производства?
   

Задача 3.

Структурная форма модели имеет вид:



Известно, что приведенная форма имеет вид:



Задание:

1. 
   Выберите метод определения структурных коэффициентов модели. Выбор обоснуйте.
   
2. 
   Определите возможные структурные коэффициенты на основе приведенной формы модели.
   

ВАРИАНТ 6.

Задача 1.

По исходным данным за 16 месяцев, представленным в таблице 15, постройте уравнение зависимости объема предложения некоторого блага Y для функционирующей в условиях конкуренции фирмы от цены X₁ этого блага и заработной платы X₂ сотрудников этой фирмы.

Таблица 15.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Y	20	35	30	45	60	69	75	90	105	110	120	130	130	130	135	140
X1	10	15	20	25	40	37	43	35	38	55	50	35	40	55	45	65
X2	12	10	9	9	8	8	6	4	4	5	3	1	2	3	1	2

Задание:

1. 
   Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
   
2. 
   Дайте экономическую интерпретацию параметров модели.
   
3. 
   Для полученной модели проверьте выполнение условия гомоскедастичности остатков, применив тест Голдфельда-Квандта.
   
4. 
   Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
   

Задача 2.

1. 
   Используя исходные данные первой задачи и учитывая изменение экономической ситуации после 8 наблюдений, проверьте с помощью теста Чоу необходимость разбиения исходной выборки на две и построения для каждой из них
   отдельного уравнения регрессии.
   
2. 
   Постройте уравнение регрессии с включением фиктивных переменных, учитывающее изменение ситуации после 8 наблюдения.
   
3. 
   Дайте экономическую интерпретацию параметров модели.
   
4. 
   Сравните качество полученной модели и модели, построенной в задаче 1.
   

Задача 3.

Структурная форма конъюнктурной модели имеет вид: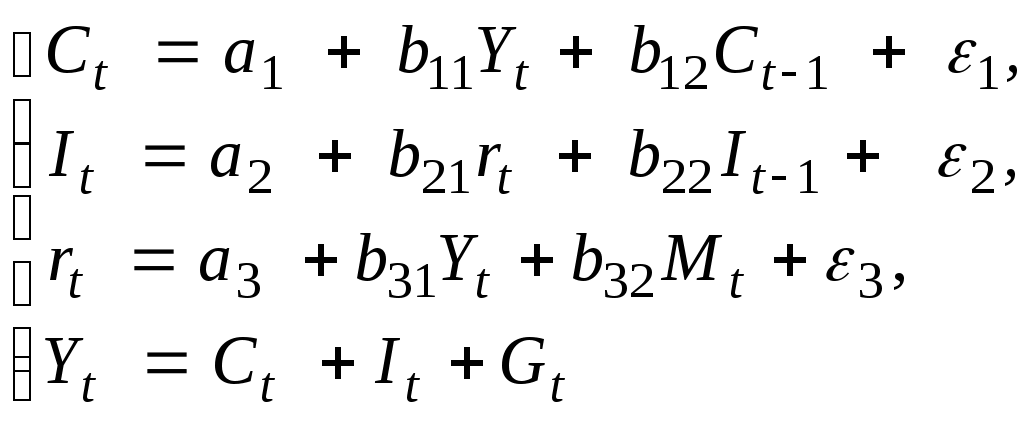



где: С_t– расходы на потребление в период t,

С_t-1– расходы на потребление в период t-1,

Y_t– ВВП в период t,

I_t – инвестиции в период t,

I_t-1 – инвестиции в период t-1,

r_t – процентная ставка в период t,

M_t – денежная масса в период t,

G_t– государственные расходы в период t,
Задание:

1. 
   Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
   
2. 
   Запишите приведенную форму модели.
   
3. 
   Определите метод оценки параметров модели.
   

ВАРИАНТ 7.

Задача 1.

По данным за два года изучается зависимость оборота розничной торговли (Y, млрд. руб.) от ряда факторов: - денежные доходы населения, млрд. руб.; Х₂ – официальный курс рубля по отношению к доллару США; Х₃ – доля доходов, используемая на покупку товаров и оплату услуг, млрд. руб.; Х₄ – индекс потребительских цен, в % к прошлому году.

Таблица 16

Месяц	Y	X1	X2	X3	X4
1	72,9	117,7	6,026	81,6	101,5
2	67,0	123,8	6,072	73,2	100,9
3	69,7	126,9	6,106	75,3	100,6
4	70,0	134,1	6,133	71,3	100,4
5	69,8	123,1	6,164	77,3	100,5
6	69,1	126,7	6,198	76,0	100,1
7	70,7	130,4	6,238	76,6	100,2
8	80,1	129,3	7,905	84,7	103,7
9	105,2	145,4	16,065	92,4	138,4
10	102,5	163,8	16,010	80,3	104,5
11	108,7	164,8	17,880	82,6	105,7
12	134,8	227,2	20,650	70,9	111,6
13	116,7	164,0	22,600	89,9	108,4
14	117,8	183,7	22,860	81,3	104,1
15	128,7	195,8	24,180	83,7	102,8
16	129,8	219,4	24,230	76,1	103,0
17	133,1	209,8	24,440	80,4	102,2
18	136,3	223,3	24,220	78,1	101,9
19	139,7	223,6	24,190	79,8	102,8
20	151,0	236,6	24,750	82,1	101,2
21	154,6	236,6	25,080	83,2	101,5
22	160,2	248,6	26,050	80,8	101,4
23	163,2	253,4	26,420	81,8	101,2
24	191,7	351,4	27,000	68,3	101,3

Задание:

1. 
   Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
   
2. 
   Выделите значимые и незначимые факторы в модели. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
   
3. 
   Рассчитайте стандартизованные коэффициенты модели и запишите уравнение регрессии в стандартизованном виде. Упорядочите факторы по степени влияния на оборот розничной торговли?
   
4. 
   Для полученной модели проверьте выполнение условия гомоскедастичности остатков, применив тест Голдфельда-Квандта.
   
5. 
   Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
   
6. 
   Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки (по первым 12 и осталь-ным наблюдениям) в одну и рассматривать единую модель регрессии Y по X?
   

Задача 2.

По данным о динамике товарооборота (Y, млрд. руб.) и дохода населения (X, млрд. руб.) была получена следующая модель с распределенными лагами:

Y_t = 0,57∙X_t + 0,24∙X_t-1+ 0,11∙X_t-2 + 0,10∙X_t-3 + ε_t.

(0,07) (0,05) (0,04) (0,03)

В скобках указаны значения стандартных ошибок для коэффициентов регрессии. Значение R² = 0,97.
Задание:

1. 
   Проанализируйте полученные результаты регрессионного анализа.
   
2. 
   Дайте интерпретацию параметров модели: определите краткосрочный и долгосрочный мультипликаторы.
   
3. 
   Определите величину среднего лага и медианного лага.
   

Задача 3.

Структурная форма модели имеет вид: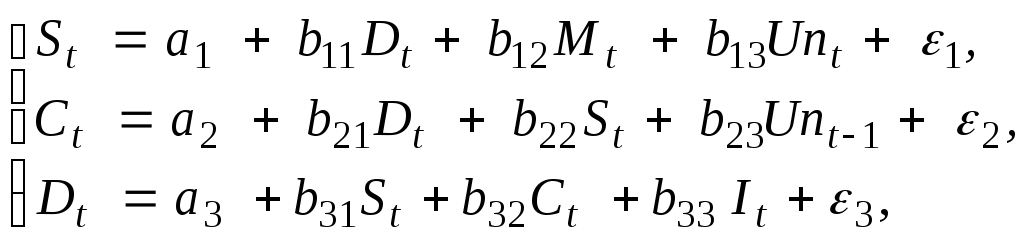



где: S_t– зарплата в период t,

D_t– чистый национальный доход в период t,

M_t – денежная масса в период t,

C_t – расходы на потребление в период t,

С_t-1 – расходы на потребление в период t-1,

Un_t – уровень безработицы в период t,

Un_t-1 – уровень безработицы в период t-1,

I_t – инвестиции в период t.
Задание:

1. 
   Проверьте каждое уравнение модели на идентифицируемость, применив необходимое и достаточное условия идентифицируемости.
   
2. 
   Запишите приведенную форму модели.
   
3. 
   Определите метод оценки структурных параметров каждого уравнения.