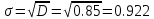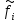3. Построим интервальный статистический ряд:
Определение числа групп:
Число групп приближенно определяется по формуле Стэрджесса
n = 1 + 3,322log n = 1 + 3,322log(100) = 8
Ширина интервала составит:
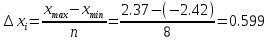
xmax - максимальное значение группировочного признака в совокупности.
xmin - минимальное значение группировочного признака.
Сгруппированный статистический ряд
Границы
интервала
|
Середина интервала, xцентр
|
Частота mi
|
Относительная частота, mi/n
|
Плотность относительной частоты 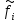
|
-2.42 - -1.821
|
-2.1205
|
3
|
0.03
|
0,050083
|
-1.821 - -1.222
|
-1.5215
|
7
|
0.07
|
0,116861
|
-1.222 - -0.623
|
-0.9225
|
9
|
0.09
|
0,15025
|
-0.623 - -0.024
|
-0.3235
|
23
|
0.23
|
0,383973
|
-0.024 - 0.575
|
0.2755
|
28
|
0.28
|
0,467446
|
0.575 - 1.174
|
0.8745
|
18
|
0.18
|
0,300501
|
1.174 - 1.773
|
1.4735
|
10
|
0.1
|
0,166945
|
1.773 - 2.372
|
2.0725
|
2
|
0.02
|
0,033389
|
Итого
|
|
100
|
1
|
|
4. Рассчитаем числовые характеристики и их оценки:
Средняя взвешенная (выборочная средняя)
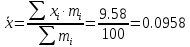
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
𝐷 =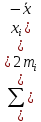 = =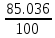 = 0.85 = 0.85
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).
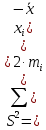 = =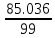 = 0.859 = 0.859
Среднее квадратическое отклонение.
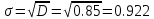
5. Выровняем статистический ряд, применяя гипотезу о том, что закон распределения случайной величины Х нормальный.
По данным интервального ряда построим гистограмму
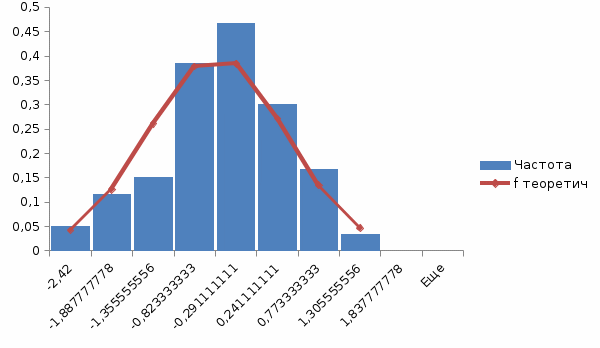
Выровняем статистический ряд с помощью нормального закона. Построим выравнивающую аналитическую кривую, совместив ее с гистограммой.
По выполненным построениям, можно выдвинуть гипотезу о том, что выборка распределена по нормальному закону распределения.
6. Проверить гипотезу с помощью критерия Колмогорова.
Выдвинем гипотезу: H0={о соответствии F*(x) и F(x) }
Проверка гипотезы с использованием критерия Колмогорова проводится для не сгруппированного статистического ряда следующим образом:
- для каждого значения сформированного статистического ряда рассчитывается значение эмпирической функции распределения вероятностей.
- рассчитывается теоретическая функция распределения вероятностей.
Все расчеты сведем в таблицу:
x
|
f
|
S
|
F(x)
|
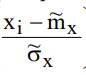
|
F*(x)
|
|F*(x)- F(x)|
|
-2,42
|
1
|
1
|
0,01
|
-2,74542
|
0,003022
|
0,006978
|
-2,02
|
1
|
2
|
0,02
|
-2,30881
|
0,010477
|
0,009523
|
-1,9
|
1
|
3
|
0,03
|
-2,17783
|
0,014709
|
0,015291
|
-1,63
|
1
|
4
|
0,04
|
-1,88311
|
0,029843
|
0,010157
|
-1,62
|
1
|
5
|
0,05
|
-1,8722
|
0,03059
|
0,01941
|
-1,52
|
1
|
6
|
0,06
|
-1,76304
|
0,038946
|
0,021054
|
-1,46
|
1
|
7
|
0,07
|
-1,69755
|
0,044796
|
0,025204
|
-1,42
|
1
|
8
|
0,08
|
-1,65389
|
0,049075
|
0,030925
|
-1,34
|
1
|
9
|
0,09
|
-1,56657
|
0,058608
|
0,031392
|
-1,33
|
1
|
10
|
0,1
|
-1,55565
|
0,059895
|
0,040105
|
-1,21
|
1
|
11
|
0,11
|
-1,42467
|
0,077126
|
0,032874
|
-1,14
|
1
|
12
|
0,12
|
-1,34826
|
0,088787
|
0,031213
|
-1,05
|
1
|
13
|
0,13
|
-1,25002
|
0,105645
|
0,024355
|
-1
|
1
|
14
|
0,14
|
-1,19545
|
0,115956
|
0,024044
|
-0,98
|
1
|
15
|
0,15
|
-1,17362
|
0,120274
|
0,029726
|
-0,9
|
1
|
16
|
0,16
|
-1,08629
|
0,138674
|
0,021326
|
-0,76
|
1
|
17
|
0,17
|
-0,93348
|
0,175286
|
0,005286
|
-0,75
|
1
|
18
|
0,18
|
-0,92256
|
0,178117
|
0,001883
|
-0,7
|
1
|
19
|
0,19
|
-0,86799
|
0,192701
|
0,002701
|
-0,57
|
1
|
20
|
0,2
|
-0,72609
|
0,233892
|
0,033892
|
-0,54
|
2
|
22
|
0,22
|
-0,69334
|
0,244047
|
0,024047
|
-0,53
|
1
|
23
|
0,23
|
-0,68243
|
0,247485
|
0,017485
|
-0,51
|
1
|
24
|
0,24
|
-0,6606
|
0,254436
|
0,014436
|
-0,48
|
1
|
25
|
0,25
|
-0,62785
|
0,265051
|
0,015051
|
-0,43
|
2
|
27
|
0,27
|
-0,57327
|
0,28323
|
0,01323
|
-0,4
|
2
|
29
|
0,29
|
-0,54053
|
0,294417
|
0,004417
|
-0,32
|
1
|
30
|
0,3
|
-0,4532
|
0,325201
|
0,025201
|
-0,29
|
2
|
32
|
0,32
|
-0,42046
|
0,337075
|
0,017075
|
-0,28
|
1
|
33
|
0,33
|
-0,40954
|
0,34107
|
0,01107
|
-0,18
|
1
|
34
|
0,34
|
-0,30039
|
0,38194
|
0,04194
|
-0,15
|
1
|
35
|
0,35
|
-0,26764
|
0,394487
|
0,044487
|
-0,12
|
3
|
38
|
0,38
|
-0,2349
|
0,407144
|
0,027144
|
-0,11
|
1
|
39
|
0,39
|
-0,22398
|
0,411385
|
0,021385
|
-0,08
|
1
|
40
|
0,4
|
-0,19124
|
0,42417
|
0,02417
|
-0,06
|
2
|
42
|
0,42
|
-0,16941
|
0,432739
|
0,012739
|
0
|
1
|
43
|
0,43
|
-0,10391
|
0,458619
|
0,028619
|
0,03
|
1
|
44
|
0,44
|
-0,07117
|
0,471632
|
0,031632
|
0,07
|
1
|
45
|
0,45
|
-0,02751
|
0,489028
|
0,039028
|
0,09
|
1
|
46
|
0,46
|
-0,00568
|
0,497736
|
0,037736
|
0,12
|
1
|
47
|
0,47
|
0,02707
|
0,510798
|
0,040798
|
0,13
|
1
|
48
|
0,48
|
0,037985
|
0,51515
|
0,03515
|
0,15
|
1
|
49
|
0,49
|
0,059816
|
0,523849
|
0,033849
|
0,16
|
1
|
50
|
0,5
|
0,070731
|
0,528194
|
0,028194
|
0,18
|
1
|
51
|
0,51
|
0,092562
|
0,536874
|
0,026874
|
0,23
|
1
|
52
|
0,52
|
0,147139
|
0,558489
|
0,038489
|
0,26
|
1
|
53
|
0,53
|
0,179885
|
0,571378
|
0,041378
|
0,29
|
1
|
54
|
0,54
|
0,212631
|
0,584192
|
0,044192
|
0,31
|
1
|
55
|
0,55
|
0,234461
|
0,592687
|
0,042687
|
0,34
|
1
|
56
|
0,56
|
0,267207
|
0,605345
|
0,045345
|
0,38
|
1
|
57
|
0,57
|
0,310869
|
0,62205
|
0,05205
|
0,4
|
1
|
58
|
0,58
|
0,332699
|
0,630319
|
0,050319
|
0,41
|
1
|
59
|
0,59
|
0,343615
|
0,634432
|
0,044432
|
0,43
|
2
|
61
|
0,61
|
0,365445
|
0,642611
|
0,032611
|
0,45
|
1
|
62
|
0,62
|
0,387276
|
0,650724
|
0,030724
|
0,47
|
1
|
63
|
0,63
|
0,409107
|
0,658769
|
0,028769
|
0,5
|
1
|
64
|
0,64
|
0,441853
|
0,670702
|
0,030702
|
0,51
|
3
|
67
|
0,67
|
0,452768
|
0,674642
|
0,004642
|
0,53
|
1
|
68
|
0,68
|
0,474599
|
0,682463
|
0,002463
|
0,54
|
1
|
69
|
0,69
|
0,485514
|
0,686344
|
0,003656
|
0,56
|
1
|
70
|
0,7
|
0,507345
|
0,694044
|
0,005956
|
0,6
|
1
|
71
|
0,71
|
0,551006
|
0,709185
|
0,000815
|
0,61
|
1
|
72
|
0,72
|
0,561921
|
0,712915
|
0,007085
|
0,62
|
1
|
73
|
0,73
|
0,572837
|
0,716622
|
0,013378
|
0,64
|
1
|
74
|
0,74
|
0,594667
|
0,723967
|
0,016033
|
0,65
|
1
|
75
|
0,75
|
0,605583
|
0,727604
|
0,022396
|
0,73
|
1
|
76
|
0,76
|
0,692905
|
0,755816
|
0,004184
|
0,75
|
2
|
78
|
0,78
|
0,714736
|
0,762614
|
0,017386
|
0,79
|
1
|
79
|
0,79
|
0,758397
|
0,775893
|
0,014107
|
0,8
|
2
|
81
|
0,81
|
0,769313
|
0,779146
|
0,030854
|
0,87
|
1
|
82
|
0,82
|
0,84572
|
0,801146
|
0,018854
|
0,92
|
1
|
83
|
0,83
|
0,900297
|
0,816019
|
0,013981
|
0,97
|
1
|
84
|
0,84
|
0,954873
|
0,830179
|
0,009821
|
0,98
|
1
|
85
|
0,85
|
0,965789
|
0,832925
|
0,017075
|
1,01
|
1
|
86
|
0,86
|
0,998535
|
0,84099
|
0,01901
|
1,1
|
1
|
87
|
0,87
|
1,096773
|
0,86363
|
0,00637
|
1,11
|
1
|
88
|
0,88
|
1,107688
|
0,866002
|
0,013998
|
1,18
|
1
|
89
|
0,89
|
1,184095
|
0,881812
|
0,008188
|
1,22
|
1
|
90
|
0,9
|
1,227757
|
0,890231
|
0,009769
|
1,23
|
1
|
91
|
0,91
|
1,238672
|
0,892267
|
0,017733
|
1,24
|
1
|
92
|
0,92
|
1,249587
|
0,894275
|
0,025725
|
1,27
|
1
|
93
|
0,93
|
1,282333
|
0,900137
|
0,029863
|
1,28
|
1
|
94
|
0,94
|
1,293249
|
0,902037
|
0,037963
|
1,31
|
1
|
95
|
0,95
|
1,325995
|
0,907579
|
0,042421
|
1,37
|
1
|
96
|
0,96
|
1,391487
|
0,917961
|
0,042039
|
1,63
|
1
|
97
|
0,97
|
1,675285
|
0,953061
|
0,016939
|
1,77
|
1
|
98
|
0,98
|
1,8281
|
0,966233
|
0,013767
|
2,12
|
1
|
99
|
0,99
|
2,210137
|
0,986452
|
0,003548
|
2,37
|
1
|
100
|
1
|
2,48302
|
0,993486
|
0,006514
|
Итого
|
100
|
|
|
|
|
max=0,05205
|
x_cp=
|
0,0952
|
|
|
|
|
|
Среднеквадратическое
|
0,916142
|
|
|
|
|
|
Критическое значение критерия λα=1,358 заданном уровне значимости α=0,05.
ΔF=0,05205
ΔF< λα
Нулевая гипотеза о соответствии F*(x) и F(x) считается правдоподобной с уровнем значимости α=0,05.
|
 Скачать 58.76 Kb.
Скачать 58.76 Kb.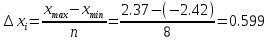
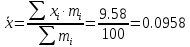
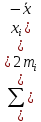 =
=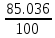 = 0.85
= 0.85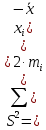 =
=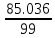 = 0.859
= 0.859